wpspectrum
Wavelet packet spectrum
Syntax
Description
[___,
returns the terminal nodes of the wavelet packet tree in frequency order.tinfo] = wpspectrum(___)
Examples
Input Arguments
Output Arguments
More About
Algorithms
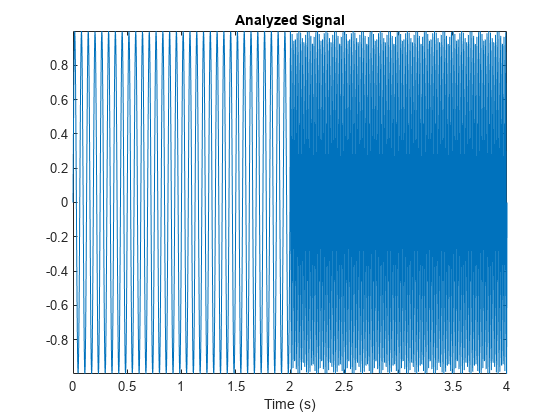
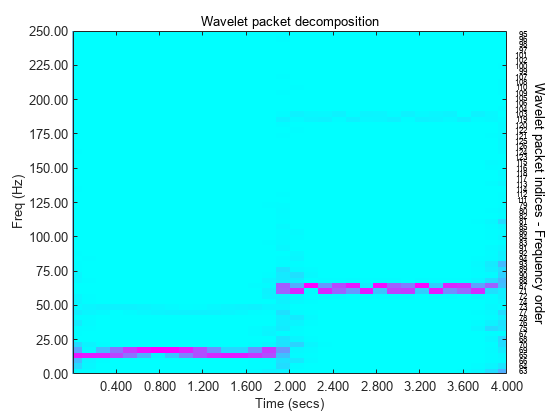
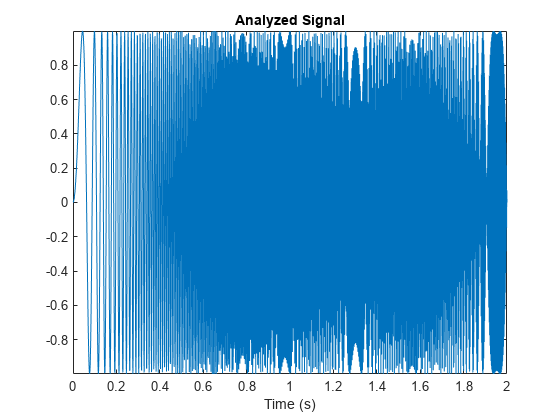
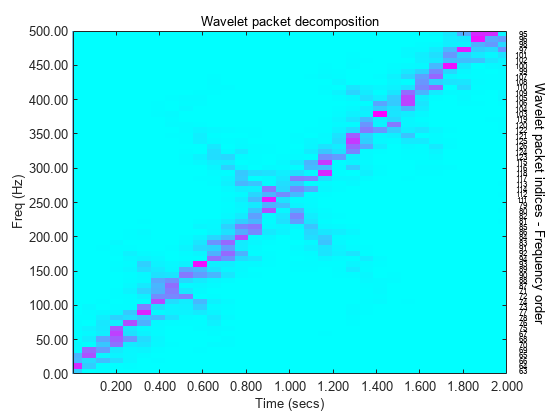
wpspectrum computes the wavelet packet spectrum as follows:
Extract the wavelet packet coefficients corresponding to the terminal nodes. Take the absolute value of the coefficients.
Order the wavelet packet coefficients by frequency ordering.
Determine the time extent on the original time axis corresponding to each wavelet packet coefficient. Repeat each wavelet packet coefficient to fill in the time gaps between neighboring wavelet packet coefficients and create a vector equal in length to node 0 of the wavelet packet tree object.
References
[1] Wickerhauser, M.V. Lectures on Wavelet Packet Algorithms, Technical Report, Washington University, Department of Mathematics, 1992.
Version History
Introduced in R2010b