wpdencmp
Denoising or compression using wavelet packets
Syntax
Description
[
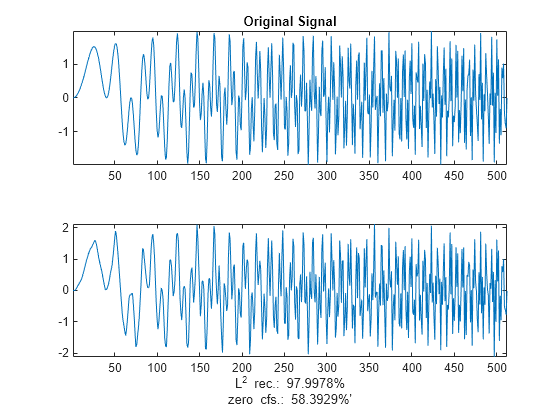
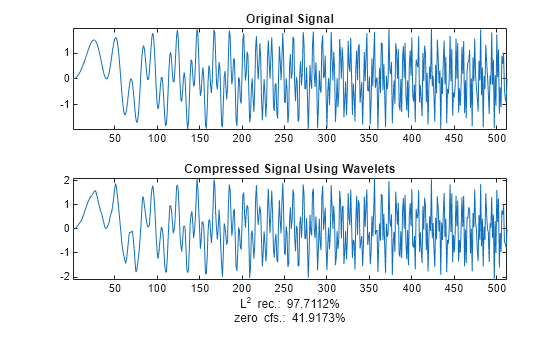
returns a denoised or compressed version xd,treed,perf0,perfl2] = wpdencmp(x,sorh,n,wname,crit,par,keepapp)xd of the input data
x obtained by wavelet packet coefficient thresholding.
wpdencmp also returns the wavelet packet best tree
decomposition treed of xd (see besttree for more information),
and the L2 energy recovery and
compression scores in percentages as perfl2 and
perf0, respectively.
Examples
Input Arguments
Output Arguments
References
[1] Antoniadis, A., and G. Oppenheim, eds. Wavelets and Statistics. Lecture Notes in Statistics. New York: Springer Verlag, 1995.
[2] Coifman, R. R., and M. V. Wickerhauser. “Entropy-Based Algorithms for Best Basis Selection.” IEEE Transactions on Information Theory. Vol. 38, Number 2, 1992, pp. 713–718.
[3] DeVore, R. A., B. Jawerth, and B. J. Lucier. “Image Compression Through Wavelet Transform Coding.” IEEE Transactions on Information Theory. Vol. 38, Number 2, 1992, pp. 719–746.
[4] Donoho, D. L. “Progress in Wavelet Analysis and WVD: A Ten Minute Tour.” Progress in Wavelet Analysis and Applications (Y. Meyer, and S. Roques, eds.). Gif-sur-Yvette: Editions Frontières, 1993.
[5] Donoho, D. L., and I. M. Johnstone. “Ideal Spatial Adaptation by Wavelet Shrinkage.” Biometrika. Vol. 81, 1994, pp. 425–455.
[6] Donoho, D. L., I. M. Johnstone, G. Kerkyacharian, and D. Picard. “Wavelet Shrinkage: Asymptopia?” Journal of the Royal Statistical Society, series B. Vol. 57, Number 2, 1995, pp. 301–369.
Version History
Introduced before R2006a