Konstant-Q-, datenadaptive und quadratische Zeit-Frequenz-Transformation
Ermitteln Sie die Konstant-Q-Transformation (CQT) eines Signals und invertieren Sie die Transformation für eine perfekte Rekonstruktion. Zerlegen Sie ein Signal mit Hilfe eines adaptiven Wavelet-Unterteilungsschemas. Führen Sie datenadaptive Zeit-Frequenz-Analysen von nichtlinearen und nichtstationären Prozessen durch. Zerlegen Sie einen nichtlinearen oder nichtstationären Prozess in seine intrinsischen Schwingungsmoden. Führen Sie eine Zeit-Frequenz-Filterung mit der diskreten Gabor-Transformation (DGT) und Gabor-Multiplikatoren durch. Erhalten Sie Schätzwerte der momentanen Frequenz eines mehrkomponentigen nichtlinearen oder nichtstationären Signals. Geben Sie die Wigner-Ville- und die Kreuz-Wigner-Ville-Verteilung der Signale zurück.
Funktionen
cqt | Constant-Q nonstationary Gabor transform |
icqt | Inverse constant-Q transform using nonstationary Gabor frames |
dgt | Discrete Gabor transform (Seit R2025a) |
tffilt | Time-frequency filtering using binary mask and Gabor transform (Seit R2025a) |
emd | Empirical mode decomposition |
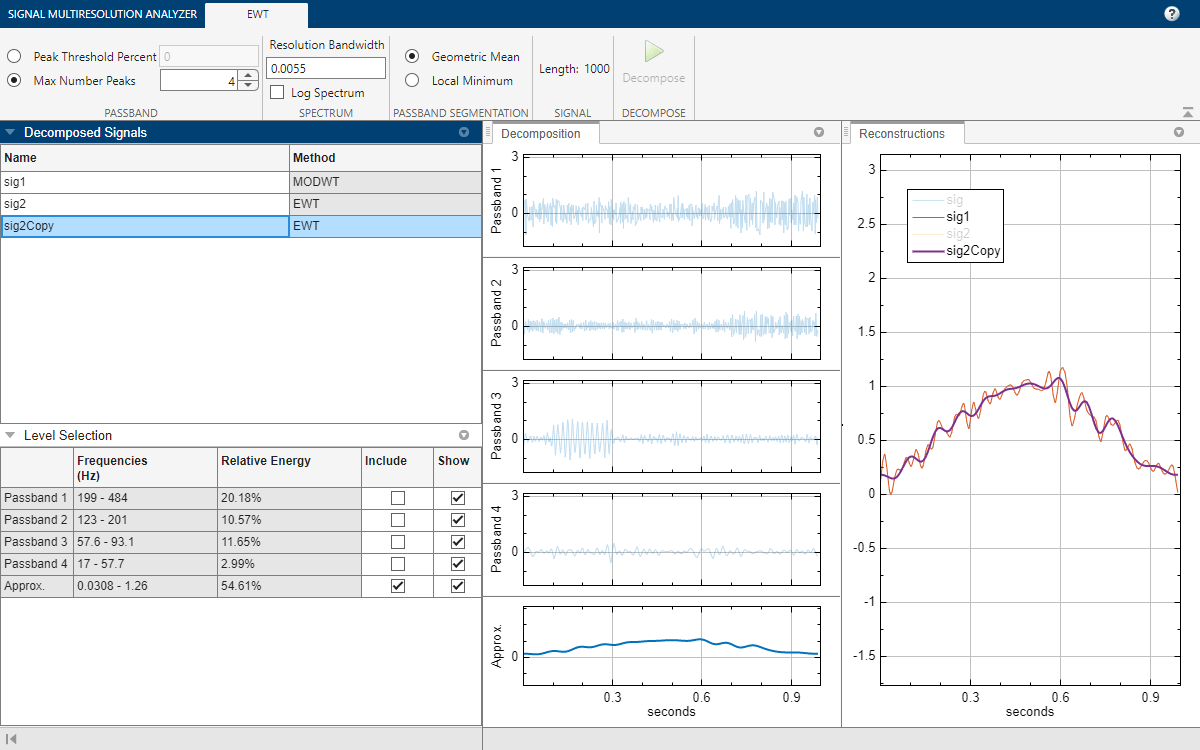
ewt | Empirical wavelet transform |
hht | Hilbert-Huang transform |
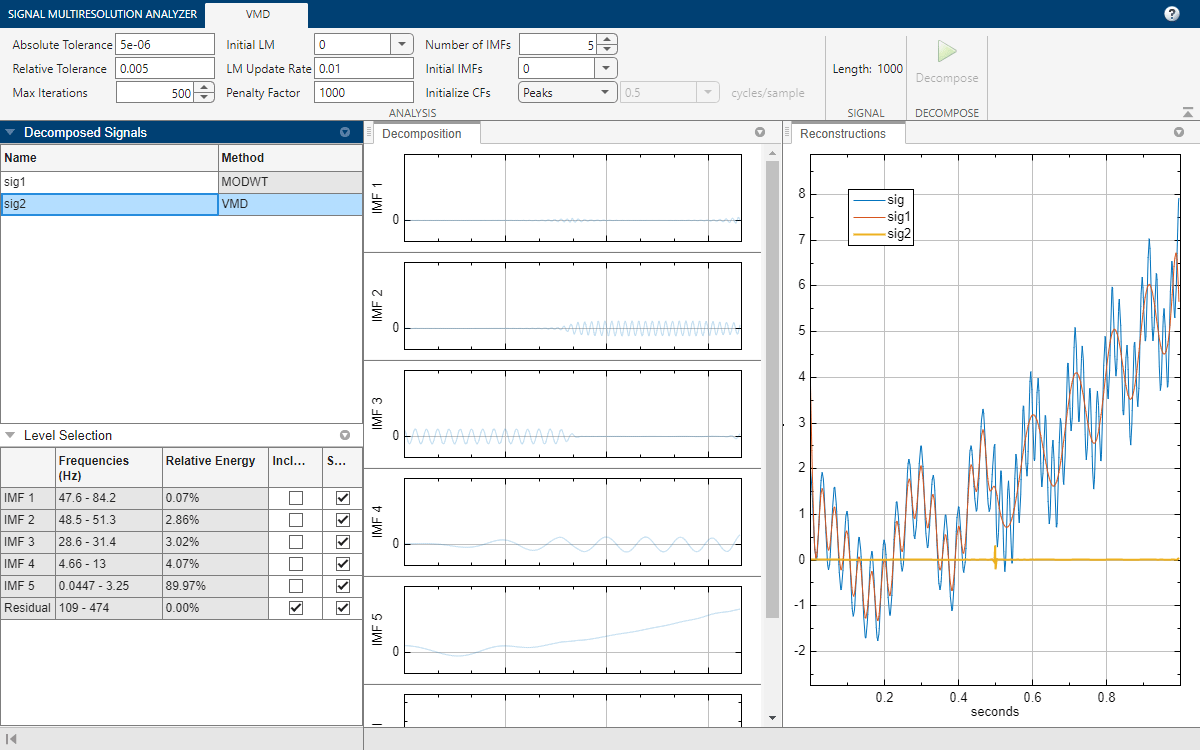
vmd | Variational mode decomposition |
wvd | Wigner-Ville distribution and smoothed pseudo Wigner-Ville distribution |
xwvd | Cross Wigner-Ville distribution and cross smoothed pseudo Wigner-Ville distribution |
Apps
| Signal Multiresolution Analyzer | Decompose signals into time-aligned components |
Themen
- Nichtstationäre Gabor-Frames und die Constant-Q-Transformation
Erfahren Sie mehr über die frequenzadaptive Analyse von Signalen.
- Empirical Wavelet Transform
Learn about the empirical wavelet transform.
Enthaltene Beispiele
Using Gabor-Based Time-Frequency Filtering for Audio Source Separation
Isolate speech in a mixed signal using a binary mask with the discrete Gabor transform.
Visualize and Recreate EWT Decomposition
Learn how to visualize an empirical wavelet transform decomposition using Signal Multiresolution Analyzer.
Visualize and Recreate VMD Decomposition
Learn how to visualize the intrinsic mode functions and residual of a variational mode decomposition using Signal Multiresolution Analyzer.
