Die Übersetzung dieser Seite ist veraltet. Klicken Sie hier, um die neueste Version auf Englisch zu sehen.

Nichtstationäre Gabor-Rahmen und die Constant-Q-Transformation

Nichtstationäre Gabor-Rahmen ermöglichen es Ihnen, zeit- oder frequenzadaptative Analysen von Signalen zu implementieren. Bei den Funktionen cqt und icqt werden nichtstationäre Gabor-Rahmen verwendet, um eine (frequenzadaptative) Constant-Q-Transformation (CQT) eines Signals zu erzielen. Eine bemerkenswerte Stärke der nichtstationären Gabor-Rahmen liegt darin, dass sie die Konstruktion stabiler Inversen ermöglichen und so eine perfekte Rekonstruktion ergeben.

Die Theorie von nichtstationären Gabor-Rahmen sowie effiziente Algorithmen zu deren Implementierung sind Dörfler, Holighaus, Grill und Velasco zu verdanken [1][2]. Die Algorithmen in [1] und [2] implementieren eine phasenstarre Version der CQT. Diese erhält nicht die dieselben Phasen aufrecht, die durch die naive Faltung erzielt werden würden. In [3] entwickeln Schörkhuber, Klapuri, Holighaus und Dörfler effiziente Algorithmen für die CQT und inverse CQT, mit denen die durch die naive Faltung erzielten Koeffizienten imitiert werden. Die große Toolbox für Zeit-Frequenz-Analysen [4] bietet eine umfangreiche Reihe von Algorithmen für die nichtstationäre Gabor-Analyse und -Synthese.

In der standardmäßigen Gabor-Analyse wird die Zeit-Frequenz-Ebene von einem Fenster fester Größe unterteilt. Ein nichtstationärer Gabor-Rahmen ist eine Sammlung von Funktionen zur Fenstererstellung in verschiedenen Größen, die dafür verwendet werden, die Zeit-Frequenz-Ebene in Fenster zu unterteilen. Die Wavelet-Analyse unterteilt die Zeit-Frequenz-Ebene auf ähnliche Weise in Fenster. Sie haben die Flexibilität, die Abtastdichte in Zeit und Frequenz zu ändern. Nichtstationäre Gabor-Rahmen sind in Bereichen wie der Verarbeitung von Audiosignalen nützlich, in denen Zeit-Frequenz-Fenster mit einer festgelegten Größe nicht optimal sind. Im Gegensatz zur Kurzzeit-Fourier-Transformation weisen die in der Constant-Q-Transformation verwendeten Fenster eine anpassbare Bandbreite und Abtastdichte auf. Im Frequenzraum sind die Fenster in logarithmisch angeordneten Mittenfrequenzen zentriert.

Zerlegen der Zeit-Frequenz-Ebene

Die Fourier-Transformation der f(t) stellt den Zusammenhang zwischen f(t) und e^{j ω t} dar:

$$F(\omega )={\displaystyle {\int }_{-\infty }^{\infty }f}(t)e^{-j\omega t}dt.$$

Da e^{j ω t} keinen kompakten Träger aufweist, stellt die Fourier-Transformation keine ideale Wahl für die Untersuchung von nichtstationären Signalen dar. Falls sich der Frequenzinhalt eines Signals mit der Zeit ändert, erfasst die Fourier-Transformation nicht, welche Änderungen das sind und wann diese auftreten. Der Teilbereich der hier dargestellten Zeit-Frequenz-Ebene zeigt dieses Verhalten der Fourier-Transformation an.

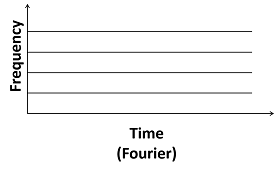
Um eine Zeit-Frequenz-Analyse eines nichtstationären Signals vorzunehmen, beginnen Sie mit einer geradzahligen, reellwertigen Fensterungsfunktion $$g(t)$$, die nur in einem endlichen Intervall effektiv größer als 0 ist und eine Norm von 1 aufweist. Darüber hinaus wird die Fourier-Transformation von $$g(t)$$ bei 0 zentriert und weist einen Tiefpass auf. Schieben Sie das Fenster f(t) über $$g(t)$$. Nehmen Sie anschließend die Fourier-Transformation des Ergebnisses vor

$$SF(u,\zeta )={\displaystyle \int f}(t)g(t-u)e^{-j\zeta t}dt.$$

Die standardmäßige Gabor-Analyse besteht darin, f(t) zu den Gabor-Atomen $$g(t-u)e^{j\zeta t}$$ in Beziehung zu setzen. Durch Verändern von u berücksichtigen Sie nur Werte von f(t) nahe des Zeitbereichs u. Der Träger von $$g(t)$$ legt die Größe der Umgebung nahe des Zeitbereichs fest u. Die Fourier-Transformation von $$g_{u,\zeta }(t)=g(t-u)e^{\zeta t}$$ ist die Translation der Fourier-Transformation von $$g(t)$$ mittels ζ und wird festgelegt durch

$${\widehat{g}}_{u,\zeta }(\omega )=e^{-(\omega -\zeta )}\widehat{g}(\omega -\zeta ).$$

Die Energiekonzentration von $${\widehat{g}}_{u,\zeta }(\omega )$$ weist eine Varianz σ_ω auf und ist bei ζ zentriert. Wenn sich das Fenster $$g_{u,\zeta }(t)=g(t-u)e^{\zeta t}$$ auf einem regelmäßigen Raster verschiebt, sind die Fourier-Transformation des Produkts des verschobenen Fensters und f(t) die Kurzzeit-Fourier-Transformation (STFT). Die STFT-Unterteilung der Zeit-Frequenz-Ebene in Fenster kann als Raster von Feldern wiedergegeben werden (u, ζ):

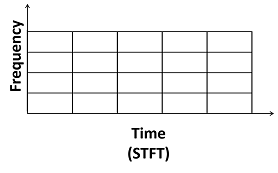
Die Reihe der Funktionen $$\left\{g_{u,\zeta }\right\}$$ wird als Gabor-Rahmen bezeichnet. Die Elemente dieser Reihe werden als Gabor-Atome bezeichnet. Bei einem Rahmen handelt es sich um eine Reihe von Funktionen, {h_k(t)}, welche die folgende Bedingung erfüllen: Es gibt Konstanten 0 < A ≤ B < ∞, sodass bei jeder Funktion Folgendes gilt f(t),

$$A\Vert f{\Vert }^2\le {\Sigma }_k|\langle f,h_k\rangle {|}^2\le B\Vert f{\Vert }^2.$$

Die Energiekonzentration von $$g(t)$$ in der Zeit weist eine Varianz σ_t auf. Die Energiekonzentration von$$\widehat{g}(\omega )$$ in der Frequenz weist eine Varianz σ_ω auf. Die Energiekonzentration legt fest, wie gut ein Fenster das Signal in Zeit und Frequenz lokalisiert. Nach dem Prinzip der Zeit-Frequenz-Unschärfe gibt es eine Beschränkung dafür, wie gut Sie gleichzeitig in den Zeit- und Frequenzebenen lokalisieren können,

wie aus Folgendem hervorgeht

$${\sigma }_t{\sigma }_{\omega }\ge \frac{1}{2}.$$

Eine Verengung des Fensters in einem Bereich führt zu einer schlechteren Lokalisierung im anderen Bereich. Gabor wies nach, dass der Bereich des Fensters am geringsten ist, wenn $$g(t)$$ eine Gauß‘sche Zahl ist.

Constant-Q-Transformation

In der CQT sind die Bandbreite und die Abtastdichte in der Frequenz unterschiedlich. Die Fenster werden konstruiert und direkt im Frequenzbereich angewendet. Verschiedene Fenster weisen unterschiedliche Mittenfrequenzen und Bandbreiten auf. Das Verhältnis der Mittenfrequenz zur Bandbreite bleibt jedoch konstant. Die Beibehaltung eines konstanten Verhältnisses setzt Folgendes voraus:

• Die Zeitauflösung verbessert sich bei höheren Frequenzen.

• Die Frequenzauflösung verbessert sich bei niedrigeren Frequenzen.

Die Zeitverschiebungen für jedes Fenster hängen aufgrund des Unschärfeprinzips von der Bandbreite ab.

Die CQT hängt von Folgendem ab:

• Die Fensterfunktionen g_k sind geradzahlige, reellwertige Funktionen. Im Frequenzbereich wird die Fourier-Transformation von g_k anhand des Intervalls [-Fs/2, Fs/2] definiert.

• Abtastrate ζ_s.

• Zahl der Intervalle pro Oktave b.

• Mindest- und Höchstfrequenzen ζ_min und ζ_max.

Wählen Sie eine Mindestfrequenz ζ_min sowie die Anzahl der Intervalle pro Oktave aus b. Bilden Sie als Nächstes eine Sequenz aus geometrisch angeordneten Frequenzen

ζ_k = ζ_min × 2^k/b

mit k = 0,...,K, wobei K eine ganze Zahl ist, sodass ζ_K als die höchste Frequenz streng kleiner als die Nyquist-Frequenz ζ_s/2 ist. Die Bandbreite der k-ten Frequenz wird auf Ω_k = ζ_k+1-ζ_k-1 festgelegt. Bei dieser Abtastung ist das Verhältnis der k-ten Mittenfrequenz zur Fensterbandbreite unabhängig von k:

Q = ζ_k/Δ_k = (2^1/b-2^-1/b)^-1.

Um eine perfekte Rekonstruktion sicherzustellen, sind die DC-Komponente und die Nyquist-Frequenz jeweils der Sequenz vorangestellt oder an sie angefügt.

W(ω) bildet die Fensterfunktionen g_k. W(ω) ist eine geradzahlige, reellwertige, stetige Funktion, die bei 0 zentriert, im Intervall [-½,½] positiv ist und an anderer Stelle 0 beträgt. W(ω) wird auf jede Mittenfrequenz ζ_{k übertragen} und dann skaliert. Die Bewertung einer skalierten und übertragenen Version von W(ω) ergibt die Filterkoeffizienten g_k[m], die aus

g_k[m] = W((m ζ_s/L - ζ_k)/Ω_k)

entstehen, mit m = 0, …, L-1, wobei L die Signallänge ist. cqt verwendet standardmäßig das Fenster 'hann'.

Aufgrund des Unschärfeprinzips schränkt die Größe der Bandbreite den Wert der Zeitverschiebungen ein. Um der Rahmenungleichheit zu entsprechen, muss die Verschiebung a_kvon g_k die Bedingung

a_k ≤ ζ_k/Ω_k.

erfüllen.

Wie bereits erwähnt, wird das Fenster im Frequenzbereich angewendet. Die Filter g_k, die bei ζ_k zentriert sind, werden gebildet und bei der Fourier-Transformation des Signals angewendet. Durch Vornehmen der inversen Transformation erhalten Sie die Constant-Q-Koeffizienten.

Referenzen

[1] Holighaus, N., M. Dörfler, G.A. Velasco, and T. Grill. "A framework for invertible real-time constant-Q transforms." IEEE Transactions on Audio, Speech, and Language Processing. Vol. 21, No. 4, 2013, pp. 775–785.

[2] Velasco, G. A., N. Holighaus, M. Dörfler, and T. Grill. "Constructing an invertible constant-Q transform with nonstationary Gabor frames." In Proceedings of the 14th International Conference on Digital Audio Effects (DAFx-11). Paris, France: 2011.

[3] Schörkhuber, C., A. Klapuri, N. Holighaus, and M. Dörfler. "A Matlab Toolbox for Efficient Perfect Reconstruction Time-Frequency Transforms with Log-Frequency Resolution." Submitted to the AES 53rd International Conference on Semantic Audio. London, UK: 2014.

[4] Průša, Z., P. L. Søndergaard, N. Holighaus, C. Wiesmeyr, and P. Balazs. The Large Time-Frequency Analysis Toolbox 2.0. Sound, Music, and Motion, Lecture Notes in Computer Science 2014, pp 419-442. https://github.com/ltfat

Siehe auch

icqt | cqt

Verwandte Themen

• Kurzzeit-Fourier-Transformation