Rotate Image by Small Acute Angle
This example shows how to implement an image rotation algorithm for small acute angles for FPGA.
Image rotation is the movement of an image around a fixed point. It is one of the most common affine transforms and is fundamental to many computer vision applications like feature extraction and matching. This equation represents the affine transform that rotates new coordinates 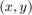 from original coordinates
from original coordinates 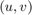 by rotation angle
by rotation angle 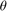 .
.
![$$ \left[{\begin{array}{cc} x\\y \end{array}}\right] = \left[{\begin{array}{ccc} cos(\theta) & -sin(\theta)\\ sin(\theta)& cos(\theta) \\ \end{array} }\right] \left[{\begin{array}{cc} u\\v \end{array}} \right] $$](../../examples/visionhdl/win64/ImageRotationHDLExample_eq06651889356311703018.png)
This implementation is based on the imrotate (Image Processing Toolbox) function.
This example computes the transformation matrix for an angle in the range (–10, 0) and (0, 10) by using the ComputeSmallAngleAffineTransform.m function. The transformation matrix returned by this function is an input to the hardware algorithm. The hardware algorithm performs an affine transform and calculates the output pixel intensities by using bilinear interpolation. This implementation does not require external DDR memory and instead uses the on-chip block RAM to store and resample the output pixel intensities.
Image Rotation Algorithm
The image rotation algorithm uses a reverse mapping technique to map the pixel locations of the output rotated image to the pixels in the input image. This diagram shows the different stages of the algorithm.
Compute Transformation This stage computes transformation parameters using the input image dimensions and the angle of rotation, 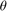 . The transformation parameters that this stage outputs include the output bounds and the transformation matrix
. The transformation parameters that this stage outputs include the output bounds and the transformation matrix 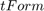 . The bounds help compute the integer pixel coordinates of the output rotated image, and
. The bounds help compute the integer pixel coordinates of the output rotated image, and 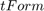 transforms the integer pixel coordinates in the output rotated image to corresponding coordinates of the input image.
transforms the integer pixel coordinates in the output rotated image to corresponding coordinates of the input image.
Affine Transform An affine transform is a geometric transformation that translates a point in one image plane onto another image plane by preserving the images collinearity. Collinearity means that all points on a line in the input image still form that line after transformation. Image rotation, maps integer pixel coordinates in the output rotated image to the corresponding coordinates of the input image by using the transformation matrix, 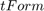 . If
. If 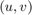 is an integer pixel coordinate in the rotated output image and
is an integer pixel coordinate in the rotated output image and 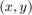 is the corresponding coordinate of the input image, then this equation describes the transformation.
is the corresponding coordinate of the input image, then this equation describes the transformation.
![$$[x \hspace{0.2cm} y \hspace{0.2cm} z]_{1X3} = [u \hspace{0.2cm} v \hspace{0.2cm} 1]_{1X3} * tForm^{-1}_{3X3}$$](../../examples/visionhdl/win64/ImageRotationHDLExample_eq15489114450813015840.png)
Bilinear Interpolation The rotation algorithm can produce 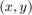 coordinates that are noninteger values. To generate the intensity of pixels at each integer position, a resampling technique like interpolation must be used. This example uses bilinear interpolation to resample the image intensity values corresponding to the generated coordinates.
coordinates that are noninteger values. To generate the intensity of pixels at each integer position, a resampling technique like interpolation must be used. This example uses bilinear interpolation to resample the image intensity values corresponding to the generated coordinates.
In the equation and the diagram, 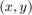 is the coordinate of the input pixel generated by the affine transform stage.
is the coordinate of the input pixel generated by the affine transform stage.  ,
,  ,
,  , and
, and 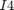 are the four neighboring pixels, and
are the four neighboring pixels, and 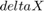 and
and  are the displacements of the target pixel from its neighboring pixels. This stage of the algorithm computes the weighted average of the four neighboring pixels by using this equation.
are the displacements of the target pixel from its neighboring pixels. This stage of the algorithm computes the weighted average of the four neighboring pixels by using this equation.
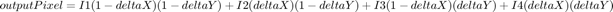
HDL Implementation
This figure shows the top-level view of the ImageRotationHDL model. The InputImage block imports the image from files. The Frame To Pixels block converts the input image frames to a pixel stream with a pixelcontrol bus for input to the ImageRotationHDLALgorithm subsystem. This subsystem rotates the input image by an angle that you can specify by using the mask of the Transform block. The Pixels To Frame block converts the stream of output pixels back to frames. The ImageViewer subsystem displays the input frame and the corresponding rotated output.
open_system('ImageRotationHDL'); set(allchild(0),'Visible','off');

The InitFcn callback of the example model computes 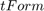 by calling the
by calling the ComputeSmallAngleAffineTransform.m function. This function takes angle of rotation and input image dimensions as the input. You can set these values in the mask of the Transform block. Alternatively, you can generate your own transformation matrix (flattened to a 6-by-1 vector, because the last column of 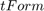 is redundant) and give it as an input to the
is redundant) and give it as an input to the ImageRotationHDLAlgorithm subsystem.
In the ImageRotationHDLAlgorithm subsystem, the GenerateControl subsystem generates a control signal pixelcontrol bus from the input ctrl bus depending upon the displacement parameter. The CoordinateGeneration subsystem generates the row and column pixel coordinates 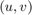 of the output rotated image. It uses two HDL counters to generate the row and column coordinates. The
of the output rotated image. It uses two HDL counters to generate the row and column coordinates. The AffineTransform subsystem maps these coordinates onto their corresponding row and column coordinates, 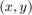 , of the input image.
, of the input image.
The AddressGeneration subsystem calculates the addresses of the four neighbors of 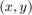 required for interpolation. This subsystem also computes the parameters
required for interpolation. This subsystem also computes the parameters 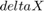 ,
,  ,
, 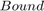 , and
, and  , which are used for bilinear interpolation.
, which are used for bilinear interpolation.
The Interpolation subsystem stores the pixel intensities of the input image in a memory. To calculate each rotated output pixel intensity, the subsystem reads the four neighbor pixel values and computes their weighted sum.
open_system('ImageRotationHDL/ImageRotationHDLAlgorithm','force');

Affine Transformation
The HDL implementation of the affine transformation multiplies the coordinates [u v 1] with the transformation matrix, 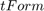 (flattened to a 6-by-1 vector, because the last column of
(flattened to a 6-by-1 vector, because the last column of 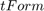 is redundant). The
is redundant). The ComputeSmallAngleAffineTransform.m function, called in the InitFcn callback of the model, generates the 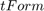 matrix. The
matrix. The Transformation subsystem implements the matrix multiplication with Product blocks which multiply the integer coordinates of output image by each element of the 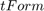 matrix. For this operation, the
matrix. For this operation, the 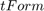 is split from a vector into individual elements by using a Demux block.
is split from a vector into individual elements by using a Demux block.
open_system('ImageRotationHDL/ImageRotationHDLAlgorithm/AffineTransform','force');

Address Generation
The AddressGeneration subsystem takes the mapped coordinate of the input raw image 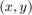 as input and then calculates the displacement
as input and then calculates the displacement 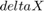 and
and  of each pixel from its neighboring pixels. The subsystem also rounds the coordinates to the nearest integer toward negative infinity.
of each pixel from its neighboring pixels. The subsystem also rounds the coordinates to the nearest integer toward negative infinity.
open_system('ImageRotationHDL/ImageRotationHDLAlgorithm/AddressGeneration','force');
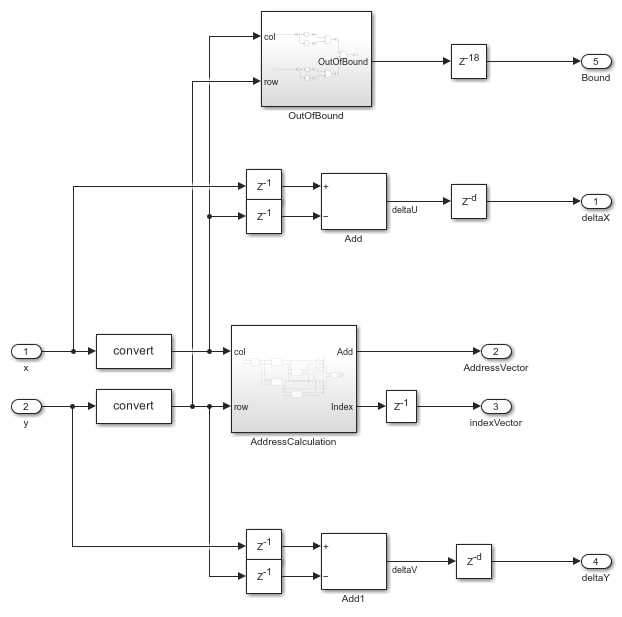
The AddressCalculation subsystem checks the coordinates against the bounds of the input images. If any coordinate is outside the image dimensions, that coordinate is capped to the boundary value for further processing. Next, the subsystem calculates the index of the address of each of the four neighborhood pixels in the CacheMemory block. The index represents the column of the cache. The subsystem finds the index for each address by using the even and odd nature of the incoming column and row coordinates, as determined by the Extract Bits block.
% ========================== % |Row || Col || Index || % ========================== % |Odd || Odd || 1 || % |Even || Odd || 2 || % |Odd || Even || 3 || % |Even || Even || 4 || % ==========================
The address of the neighborhood pixels is generated using this equation.
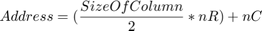
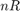 is the row coordinate and
is the row coordinate and  is the column coordinate. When
is the column coordinate. When 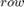 is even, then
is even, then 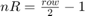 . When
. When 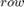 is odd, then
is odd, then  . When
. When 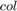 is even, then
is even, then 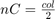 . When
. When 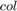 is odd, then
is odd, then  .
.
The IndexChangeForMemoryAccess MATLAB Function block in the AddressCalculation subsystem rearranges the addresses in increasing order of their indices. This operation ensures the correct fetching of data from the CacheMemory block. The addresses are given as input to the CacheMemory block, and 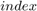 ,
, 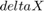 , and
, and  are passed to the
are passed to the Interpolation subsystem.
The OutOfBound subsystem checks whether the 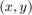 coordinates are out of bounds (that is, if any coordinate is outside the image dimensions). If the coordinate is out of bounds, the corresponding output pixel is set to an intensity value of 0.
coordinates are out of bounds (that is, if any coordinate is outside the image dimensions). If the coordinate is out of bounds, the corresponding output pixel is set to an intensity value of 0.
After all of the addresses and their corresponding indices are generated, a Vector Concatenate block creates vectors of the addresses and indices.
Interpolation
The Interpolation subsystem is a For Each block which replicates its operation depending on the dimensions of the input pixel. For example, if the input is an RGB image, then the input pixel dimensions are 1-by-3, and the model includes 3 instances of this operation. Using the For Each block enables the model to support RGB input or grayscale input. The operation inside the For Each subsystem comprises two subsystems: BilinearInterpolation and CacheMemory.
open_system('ImageRotationHDL/ImageRotationHDLAlgorithm/Interpolation','force');

Cache Memory
The CacheMemory subsystem contains a Simple Dual Port RAM block. The subsystem buffers the input pixels to form [Line 1 Pixel 1 | Line 2 Pixel 1 | Line 1 Pixel 2 | Line 2 Pixel 2] in the RAM. This configuration enables the algorithm to read all four neighboring pixels in one cycle. The required size of the cache memory is calculated from the offset output of the ComputeSmallAngleAffineTransform.m function. The offset is the sum of maximum deviation and the first row map. The first row map is the maximum value of the input image row coordinate that corresponds to the first row of the output rotated image. The maximum deviation is the greatest difference between the maximum and minimum row coordinates for each row of the input image row map.
The WriteControl subsystem forms vectors of incoming pixels, write enables, and write addresses. The AddressGeneration subsystem provides a vector of read addresses. The vector of pixels that are read from the RAM becomes the input to the BilinearInterpolation subsystem.
open_system('ImageRotationHDL/ImageRotationHDLAlgorithm/Interpolation/CacheMemory','force');

Bilinear Interpolation
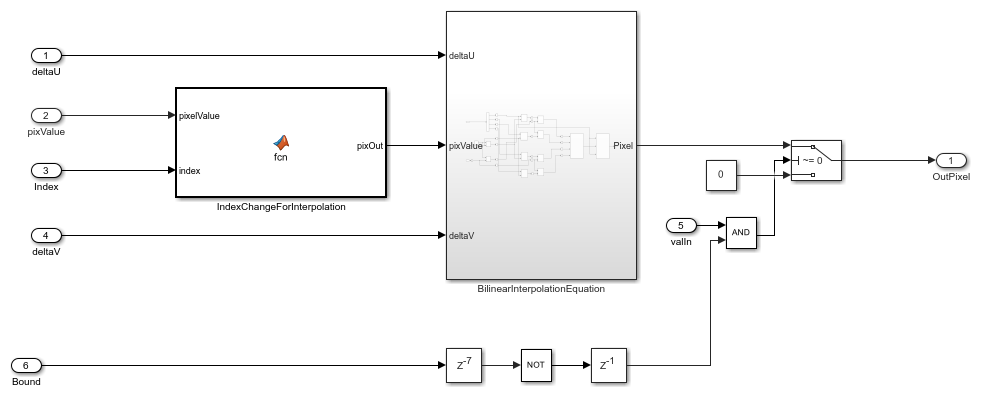
The BilinearInterpolation subsystem rearranges the vector of read pixels from the cache to their original indices. Then, the BilinearInterpolationEquation subsystem calculates a weighted sum of the neighborhood pixels by using the bilinear interpolation equation mentioned in the Image Rotation Algorithm section. The result of the interpolation is the value of the output rotated pixel.
open_system('ImageRotationHDL/ImageRotationHDLAlgorithm/Interpolation/BilinearInterpolation','force');
Simulation and Results
This example uses a 480p RGB input image. The input pixels use the uint8 data type. The example supports either grayscale or RGB input images. This example supports acute angles in the range (–10, 0) and (0, 10). Angles greater than 10 degrees require much higher BRAM resources.
This figure shows the input image and the corresponding output image rotated by an angle of 7 degrees. The results of the ImageRotationHDL model for this input matches the output of the imrotate function.
To check and generate the HDL code referenced in this example, you must have the HDL Coder™ product.
To generate the HDL code, enter this command.
makehdl('ImageRotationHDL/ImageRotationHDLAlgorithm')
To generate the test bench, enter this command.
makehdltb('ImageRotationHDL/ImageRotationHDLAlgorithm')
This design was synthesized using AMD® Vivado® for the ZC706 device and met a timing requirement of over 200 MHz. This table shows the resource utilization for the HDL subsystem.
% =============================================================== % |Model Name || ImageRotationHDL || % =============================================================== % |Input Image Resolution || 480 x 640 || % |LUT || 2238 || % |FF || 2570 || % |BRAM || 96 || % |Total DSP Blocks || 94 || % ===============================================================