mad
Mean or median absolute deviation
Description
y = mad(X)X.
If
Xis a vector, thenmadreturns the mean or median absolute deviation of the values inX.If
Xis a matrix, thenmadreturns a row vector containing the mean or median absolute deviation of each column ofX.If
Xis a multidimensional array, thenmadoperates along the first nonsingleton dimension ofX.
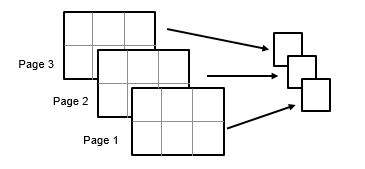
y = mad(X,flag,vecdim)vecdim. For example, if X is a 2-by-3-by-4 array,
then mad(X,0,[1 2]) returns a 1-by-1-by-4 array. Each element of the
output array is the mean absolute deviation of the elements on the corresponding page of
X.
Examples
Input Arguments
Output Arguments
Tips
For normally distributed data, multiply
madby one of the following factors to obtain an estimate of the normal scale parameter σ:sigma = 1.253 * mad(X,0)— For mean absolute deviationsigma = 1.4826 * mad(X,1)— For median absolute deviation
Algorithms
References
[1] Mosteller, F., and J. Tukey. Data Analysis and Regression. Upper Saddle River, NJ: Addison-Wesley, 1977.
[2] Sachs, L. Applied Statistics: A Handbook of Techniques. New York: Springer-Verlag, 1984, p. 253.
Extended Capabilities
Version History
Introduced before R2006a