gagerr

Gage repeatability and reproducibility study

Syntax

gagerr(y,{part,operator})

gagerr(y,group)

gagerr(y,part)

gagerr(tbl,yvar,partvar)

gagerr(tbl,yvar,partvar,opvar)

gagerr(___,Name=Value)

gagerr(ax,___)

results = gagerr(___)

[results,stats] = gagerr(___)

Description

gagerr(y,{part,operator}) performs a Gage repeatability and reproducibility (R&R) study on the measurements y, collected by operator on part.

gagerr(y,group) performs an R&R study on the measurements y, where the numeric identifiers for the parts and operators are contained in the first and second columns, respectively, of the matrix group.

gagerr(y,part) performs an R&R study on the measurements y, collected on part. Use this syntax when all measurements are collected by a single operator.

gagerr(tbl,yvar,partvar) performs an R&R study on the data in the table tbl, using the measurements in the yvar variable and the parts in the partvar variable. (since R2025a)

gagerr(tbl,yvar,partvar,opvar) performs an R&R study on the data in the table tbl, using the measurements in the yvar variable, the parts in the partvar variable, and the operators in the opvar variable. (since R2025a)

gagerr(___,Name=Value) specifies options using one or more name-value arguments in addition to any of the input argument combinations in the previous syntaxes. For example, you can specify whether to display a bar graph of results, and set the specification limits for the precision-to-tolerance ratio (PTR) calculation.

gagerr(ax,___) plots into the axes specified by ax instead of the current axes (gca). (since R2024a)

results = gagerr(___) returns the study results in results. If you specify tbl or OutputFormat="table", then results is a table. Otherwise, results is a matrix.

[results,stats] = gagerr(___) additionally returns the structure stats, which contains the number of distinct categories, the percentage of Gage R&R of total variations, the PTR, and the study variance multiplier. If you do not set the specification limits (Spec), the PTR value is NaN.

Examples

Gage Repeatability and Reproducibility Study

Simulate a measurement data set by randomly generating 100 measurements y of three parts. Each measurement is collected by one of four randomly assigned operators.

rng(1234,"twister"); % For reproducibility
n = 100;
y = randn(n,1);                
part = randi([1,3],1,n);       
operator = randi([1,4],1,n);   

Perform a Gage repeatability and reproducibility (R&R) study on this data set using a mixed ANOVA model without interactions.

gagerr(y,{part,operator},RandomOperator=false)

         Source          Variance     PercentVariance     Sigma     StudyVariation    PercentStudyVariation
    _________________    _________    _______________    _______    ______________    _____________________

    Gage R&R               0.95348         99.251        0.97646        5.0288               99.625        
      Repeatability        0.95348         99.251        0.97646        5.0288               99.625        
      Reproducibility            0              0              0             0                    0        
    Part                 0.0071911        0.74854         0.0848       0.43672               8.6518        
    Total                  0.96067            100        0.98014        5.0477                             

Study Variation: 5.15*Sigma
Number of distinct categories (NDC):0
% of Gage R&R of total variations (PRR): 99.63
Note: The last column of the above table does not have to sum to 100%

The software displays information and a bar graph summarizing the study results. Each row of the table contains statistics for a different source of variability in the measurement data. In this data set, the dominant source of variability is repeatability (the variation in the measurement value on the same part, obtained by the same operator). This source is responsible for 99.25% of the total measurement variance, and 99.63% of the total measurement standard deviation. The number of distinct categories is 0, indicating that the measurement system is not capable of distinguishing any groups within the measurement data.

Part-Nested Gage Repeatability and Reproducibility Study

Simulate a measurement data set by randomly generating 100 measurements y of five parts by three operators named A, B, and C. Each part is measured by one operator only.

rng(1234,"twister"); % For reproducibility
n = 100;
y = randn(n,1);
parts = randi(5,1,n)';
operatorName = ["A","B","C","A","A"];
operators = operatorName(parts)';
tbl = table(y,parts,operators, ...
    VariableNames=["y","Part","Operator"]);

Display the top rows of the data set.

head(tbl)

       y        Part    Operator
    ________    ____    ________

    -0.94725     1        "A"   
     0.54015     3        "C"   
     -0.2166     1        "A"   
       1.189     5        "A"   
       1.317     2        "B"   
    -0.40563     1        "A"   
    -0.44491     3        "C"   
      1.3284     5        "A"   

Perform a Gage repeatability and reproducibility (R&R) study on this data set using a mixed ANOVA model where Part is nested in Operator. Display the ANOVA table in a figure, and set SigmaMultiplier=6 to perform a six-sigma study.

gagerr(tbl,"y","Part","Operator",Model="part-nested", ...
    DisplayANOVA="on",SigmaMultiplier=6)

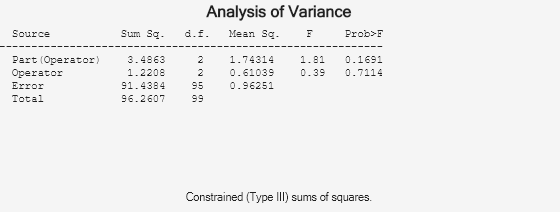
         Source          Variance    PercentVariance     Sigma     StudyVariation    PercentStudyVariation
    _________________    ________    _______________    _______    ______________    _____________________

    Gage R&R              0.96251        96.475         0.98108        5.8865               98.221        
      Repeatability       0.96251        96.475         0.98108        5.8865               98.221        
      Reproducibility           0             0               0             0                    0        
    Part                 0.035173        3.5255         0.18754        1.1253               18.776        
    Total                 0.99768           100         0.99884         5.993                             

Study Variation: 6.00*Sigma
Number of distinct categories (NDC):0
% of Gage R&R of total variations (PRR): 98.22
Note: The last column of the above table does not have to sum to 100%

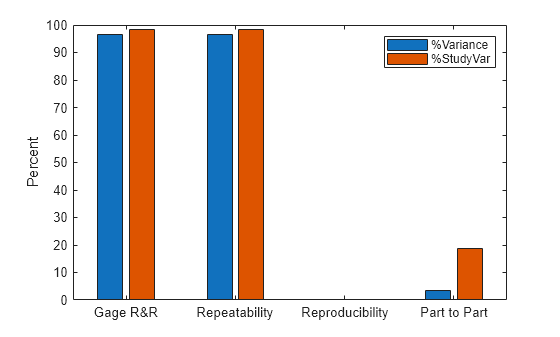
The software displays information and a bar graph summarizing the study results. Each row of the table contains statistics for a different source of variability in the measurement data. In this data set, the dominant source of variability is repeatability (the variation in the measurement value on the same part, obtained by the same operator). This source is responsible for 96.475% of the total measurement variance, and 98.1% of the total measurement standard deviation. The number of distinct categories is 0, indicating that the measurement system is not capable of distinguishing any groups within the measurement data.

Input Arguments

y — Measurements

numeric column vector

Measurements, specified as a numeric column vector.

Data Types: single | double

part — Parts

categorical array | character array | string array | logical column vector | numeric column vector | cell array of character vectors

Parts, specified as a categorical, character, or string array, a logical or numeric column vector, or a cell array of character vectors. part must have the same size as y. Each element of part contains an identifier for the part associated with the corresponding measurement in y.

Data Types: categorical | char | string | logical | single | double | cell

operator — Operators

categorical array | character array | string array | logical column vector | numeric column vector | cell array of character vectors

Operators, specified as a categorical, character, or string array, a logical or numeric column vector, or a cell array of character vectors. operator must have the same size as y. Each element of operator contains an identifier for the operator that collects the corresponding measurement in y.

Data Types: categorical | char | string | logical | single | double | cell

group — Parts and operators

n-by-2 numeric matrix

Parts and operators, specified as an n-by-2 numeric matrix, where n is the length of y. The first and second columns of group contain numeric identifiers for the part and operator, respectively, corresponding to the measurements in y.

Data Types: single | double

tbl — Input data

table

Since R2025a

Input data, specified as a table. tbl must have a variable that contains the measurements, a variable that contains the parts, and (optionally) a variable that contains the operators.

Data Types: table

yvar — Measurements variable

character array | string array

Since R2025a

Measurements variable, specified as a character or string array. yvar must be the name of the variable in tbl that contains the measurements.

Data Types: char | string

partvar — Parts variable

character array | string array

Since R2025a

Parts variable, specified as a character or string array. partvar must be the name of the variable in tbl that contains the parts.

Data Types: char | string

opvar — Operators variable

character array | string array

Since R2025a

Operators variable, specified as a character or string array. opvar must be the name of the variable in tbl that contains the operators. If you do not specify opvar, the software assumes that all measurements are obtained by a single operator.

Data Types: char | string

ax — Target axes

Axes object

Axes for the plot, specified as an Axes object. If you do not specify ax, then gagerr creates the plot using the current axes. For more information on creating an Axes object, see axes.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: results=gagerr(y,group,PrintTable="off") suppresses the command-line output.

SigmaMultiplier — Study variance multiplier

5.15 (default) | positive scalar

Since R2025a

Study variance multiplier, specified as a positive scalar. gagerr uses SigmaMultiplier to calculate the study variance and the precision-to-tolerance ratio. The default value 5.15 corresponds to the number of standard deviations that span the middle 99% of a normally distributed population.

Example: SigmaMultiplier=6

Data Types: single | double

Model — ANOVA model type

"linear" (default) | "interaction" | "nested" | "part-nested"

ANOVA model type, specified as one of the values in this table.

Value	Description
"linear" (default)	Main effects only
"interaction"	Main effects plus two-factor interactions between operator and part
"nested"	operator is nested in part. Use this model when operators are assigned to specific parts, and the operators measure only those specific parts. For more information, see Other ANOVA Models.
"part-nested" (since R2025a)	part is nested in operator. Use this model when each part is measured by a specific operator only. For more information, see Other ANOVA Models.

If you specify "linear" or "interaction", gagerr calls the anovan function with the specified value of Model.

If you specify "nested", gagerr calls anovan with model="linear" and nested=[0 0; 1 0].

If you specify "part-nested", gagerr calls anovan with model="linear" and nested=[0 1; 0 0].

If you specify part but do not specify operator in the call to gagerr, you cannot specify "interaction", "nested", or "part-nested".

Example: Model="interaction"

Data Types: char | string

RandomOperator — Indicator for random operators

true or 1 (default) | false or 0

Indicator for random operators, specified as a numeric or logical 1 (true) or 0 (false). If you specify RandomOperator=false, the software uses a mixed-effects model, where part is a random effect and operator is a fixed effect.

Example: RandomOperator=false

Data Types: logical

Spec — Lower and upper specification limits

[] (default) | two-element numeric vector

Lower and upper specification limits, specified as a two-element numeric vector. If you specify Spec, the software computes the precision-to-tolerance ratio (PTR) using the formula $$\text{PTR}=k{\sigma }_{\text{GRR}}/|({\text{S}}_2-{\text{S}}_1)|$$, where k is the value of SigmaMultiplier, σ_GRR is the Gage R&R standard deviation, and S₁ and S₂ are the first and second elements of Spec, respectively. If you do not specify Spec, PTR is NaN. For more information about PTR, see Gage R&R Study.

Example: Spec=[0.1 0.9]

Data Types: single | double

DisplayANOVA — Flag to display ANOVA table

"off" (default) | "on"

Since R2025a

Flag to display the ANOVA table, specified as "on" or "off". If you specify DisplayANOVA="on", the software displays the ANOVA table as a figure.

Example: DisplayANOVA="on"

Data Types: char | string

PrintTable — Flag to display results output

"on" (default) | "off"

Flag to display the results output, specified as "on" or "off". For more information about the results output, see Gage R&R Study.

Example: PrintTable="off"

Data Types: char | string

OutputFormat — Results output format

"table" | "matrix"

Since R2025a

Results output format, specified as "table" or "matrix". The value of OutputFormat determines whether results is a table or a matrix. If you do not specify OutputFormat, then results is a matrix if you specify y, and a table if you specify tbl.

Example: OutputFormat="matrix"

Data Types: char | string

PrintGraph — Flag to display bar graph of results

"on" (default) | "off"

Flag to display a bar graph of the results, specified as "on" or "off". For more information about the bar graph results, see Gage R&R Study.

Example: PrintGraph="off"

Data Types: char | string

Output Arguments

results — Study results

numeric matrix | table

Study results, returned as a numeric matrix or a table. If results is a matrix, the rows contain metrics for individual sources of variability in the measurement system. If you specify tbl or OutputFormat="table", then results is a table. The rows of results (or row names, if results is a table) are described below. Depending on the other options you specify, some rows are not included when results is a table.

Row	Table Row Name	Description
Gage R&R	GageRR	Total measurement variation due to repeatability and reproducibility sources
Repeatability	Gage_Repeatability	Variation in the measurements of the same part, collected by the same operator
Reproducibility	Gage_Reproducibility	Variation in the measurements of the same part, collected by different operators
Operator	Reproducibility_Operator	Variation in the measurements collected by the same operator
Part*Operator	Reproducibility_PartandOperator	Variation in the measurements due to the two-factor interactions of parts and operators. The variation is zero unless Model is "interaction".
Part-to-part	Part	Variation among the set of parts
Total	Total	Combined Gage R&R and part-to-part variability. This row is not included when results is a matrix.

The columns or variables in results are described below. The variable Source is not included when results is a table.

Column or Variable	Description
Source	Variability source
Variance	Variance
PercentVariance	Percentage of the total variance
Sigma	Standard deviation (square root of the variance)
StudyVariation	Study variance, equal to SigmaMultiplier times the standard deviation
PercentStudyVariation	Percentage of the total study variance

stats — Summary statistics

structure

Summary statistics, returned as a structure with these fields:

• ndc — Number of distinct categories

• prr — Percentage of Gage R&R of total variations

• ptr — Precision-to-tolerance ratio

• SigmaMultiplier — Study variance multiplier

If you do not specify Spec, then ptr is NaN. For more information on the summary statistics, see Gage R&R Study.

More About

Gage R&R Study

A Gage repeatability and reproducibility (R&R) study uses one- or two-way analysis of variance (see anovan) to assess the precision of a measurement system. In a typical system, a group of operators use gages to obtain multiple measurements of a set of items (parts) under the same conditions, if possible. If a system has high precision, the measurements of an individual part are narrowly scattered around a single value. There are several possible sources of variability in a measurement system.

Variability Source	Description
Repeatability	Variation in the measurements of the same part, collected by the same operator
Operator	Variation in the measurements collected by the same operator
Part*Operator	Variation in the measurements due to the interactions of parts and operators
Reproducibility	Sum of Operator and Part*Operator
Gage R&R	Total measurement variation due to repeatability and reproducibility
Part-to-part	Variation among the set of parts.

The total variability in a measurement system is the sum of Gage R&R variability and part-to-part variability.

Each of the variability sources can be characterized by a statistical metric. Common metrics are the variance, standard deviation (square root of the variance), percentage of the total variance, and percentage of the total standard deviation. The study variance is a measure of all variability in the measurement system due to repeatability and reproducibility, and is defined as the study variance multiplier (SigmaMultiplier) times the Gage R&R standard deviation. The default multiplier value 5.15 corresponds to the number of standard deviations that span the middle 99% of a normally distributed population.

Three common summary metrics describe the capability of a measurement system to distinguish the parts from each other, based on the measurement data:

• The number of distinct categories (NDC) is a measure of how many groups the system can distinguish within the measurement data. NDC is equal to $$\sqrt{2}$$ times the ratio of part-to-part standard deviation to Gage R&R standard deviation. An NDC value of 5 or larger is indicative of a capable measurement system. A system with an NDC value smaller than 2 is not capable. For example, if a measurement system has NDC=3, the measurements can be divided into three groups, such as low, middle, and high.

• The percentage of Gage R&R of total variations (PRR) is the fraction of the total standard deviation that is due to Gage R&R variability. In general, a system with PRR less than 10% is capable, while a PRR value greater than 30% indicates that the system is not capable.

• The precision-to-tolerance ratio (PTR) compares the variability in the measurement system to the specified tolerance (Spec). In general, a system with PTR less than 0.1 is capable, while a PTR value greater than 0.3 indicates that the system is not capable. For example, if the lower and upper specification limits for the set of parts are 1 and 20, respectively, and the standard deviation of the measurements due to Gage R&R is 0.3, the PTR value is 0.08, indicating a capable system.

References

[1] Burdick, Richard K., Connie M. Borror, and Douglas C. Montgomery. Design and Analysis of Gauge R&R Studies: Making Decisions with Confidence Intervals in Random and Mixed ANOVA Models. ASA-SIAM Series on Statistics and Applied Probability. Philadelphia, Pa. : Alexandria, Va: Society for Industrial Applied Mathematics ; American Statistical Association, 2005.

Version History

Introduced in R2006b

R2025a: Use extensions to gagerr

gagerr has several extensions and new syntaxes:

• You can specify input data as a table that contains a variable for the measurements, a variable for the parts, and (optionally) a variable for the operators.

• When you specify input data as a table, or set the OutputFormat name-value argument as "table", the results output is returned as a table instead of a matrix.

• You can specify the SigmaMultiplier name-value argument, which gagerr uses to calculate the study variance and the precision-to-tolerance ratio. The default value 5.15 is used in previous releases, and corresponds to the number of standard deviations that span the middle 99% of a normally distributed population.

• You can specify DisplayANOVA="on" to display the ANOVA table as a figure.

• Specify Model="part-nested" to select an ANOVA model where the parts are nested within the operators.

R2024a: Specify target axes

Specify the target axes for the plot by using the ax input argument.