crosstab
Cross-tabulation
Syntax
Description
tbl = crosstab(___,Name=Value)
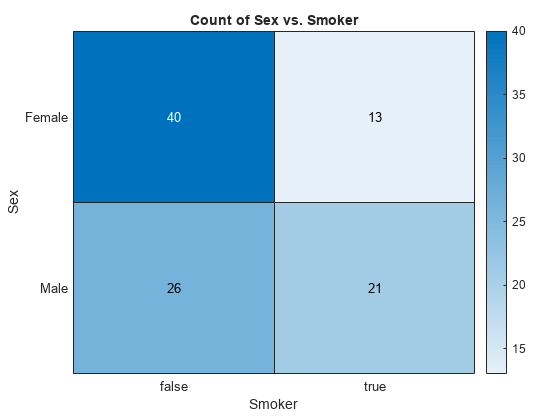
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
crosstabusesgrp2idxto assign a positive integer to each distinct value.tbl(i,j)is a count of indices wheregrp2idx(x1)isiandgrp2idx(x2)isj. The numerical order ofgrp2idx(x1)andgrp2idx(x2)order rows and columns oftbl, respectively.In this case, the returned value of
tbl(i,j,...,n)is a count of indices wheregrp2idx(x1)isi,grp2idx(x2)isj,grp2idx(x3)isk, and so on.crosstabcomputes the p-value of the chi-square test statistic using a formula that is asymptotically valid for a large sample size. The approximation is less accurate for small samples or samples with uneven marginal distributions. If your sample includes only two variables and each has two levels, you can usefishertestinstead. This function performs Fisher’s exact test, which does not depend on large-sample distribution assumptions.