edge
Class: ClassificationLinear
Classification edge for linear classification models
Description
e = edge(Mdl,Tbl,ResponseVarName)Mdl using the predictor data in
Tbl and the class labels in
Tbl.ResponseVarName.
e = edge(___,Name,Value)
Note
If the predictor data X or the predictor variables in
Tbl contain any missing values, the
edge function can return NaN. For more
details, see edge can return NaN for predictor data with missing values.
Input Arguments
Binary, linear classification model, specified as a ClassificationLinear model object.
You can create a ClassificationLinear model object
using fitclinear.
Predictor data, specified as an n-by-p full or sparse matrix. This orientation of X indicates that rows correspond to individual observations, and columns correspond to individual predictor variables.
Note
If you orient your predictor matrix so that observations correspond to columns and specify 'ObservationsIn','columns', then you might experience a significant reduction in computation time.
The length of Y and the number of observations
in X must be equal.
Data Types: single | double
Class labels, specified as a categorical, character, or string array; logical or numeric vector; or cell array of character vectors.
The data type of
Ymust be the same as the data type ofMdl.ClassNames. (The software treats string arrays as cell arrays of character vectors.)The distinct classes in
Ymust be a subset ofMdl.ClassNames.If
Yis a character array, then each element must correspond to one row of the array.The length of
Ymust be equal to the number of observations inXorTbl.
Data Types: categorical | char | string | logical | single | double | cell
Sample data used to train the model, specified as a table. Each row of
Tbl corresponds to one observation, and each column corresponds
to one predictor variable. Optionally, Tbl can contain additional
columns for the response variable and observation weights. Tbl must
contain all the predictors used to train Mdl. Multicolumn variables
and cell arrays other than cell arrays of character vectors are not allowed.
If Tbl contains the response variable used to train Mdl, then you do not need to specify ResponseVarName or Y.
If you train Mdl using sample data contained in a table, then the input
data for edge must also be in a table.
Response variable name, specified as the name of a variable in Tbl. If Tbl contains the response variable used to train Mdl, then you do not need to specify ResponseVarName.
If you specify ResponseVarName, then you must specify it as a character
vector or string scalar. For example, if the response variable is stored as
Tbl.Y, then specify ResponseVarName as
'Y'. Otherwise, the software treats all columns of
Tbl, including Tbl.Y, as predictors.
The response variable must be a categorical, character, or string array; a logical or numeric vector; or a cell array of character vectors. If the response variable is a character array, then each element must correspond to one row of the array.
Data Types: char | string
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Predictor data observation dimension, specified as 'rows' or
'columns'.
Note
If you orient your predictor matrix so that observations correspond to columns and
specify 'ObservationsIn','columns', then you might experience a
significant reduction in computation time. You cannot specify
'ObservationsIn','columns' for predictor data in a
table.
Data Types: char | string
Observation weights, specified as the comma-separated pair consisting of
'Weights' and a numeric vector or the name of a
variable in Tbl.
If you specify
Weightsas a numeric vector, then the size ofWeightsmust be equal to the number of observations inXorTbl.If you specify
Weightsas the name of a variable inTbl, then the name must be a character vector or string scalar. For example, if the weights are stored asTbl.W, then specifyWeightsas'W'. Otherwise, the software treats all columns ofTbl, includingTbl.W, as predictors.
If you supply weights, then for each regularization strength,
edge computes the weighted classification
edge and normalizes weights to sum up to the value of the
prior probability in the respective class.
Data Types: double | single
Output Arguments
Classification edges, returned as a numeric scalar or row vector.
e is the same size as Mdl.Lambda. e( is
the classification edge of the linear classification model trained
using the regularization strength j)Mdl.Lambda(.j)
Examples
Load the NLP data set.
load nlpdataX is a sparse matrix of predictor data, and Y is a categorical vector of class labels. There are more than two classes in the data.
The models should identify whether the word counts in a web page are from the Statistics and Machine Learning Toolbox™ documentation. So, identify the labels that correspond to the Statistics and Machine Learning Toolbox™ documentation web pages.
Ystats = Y == 'stats';Train a binary, linear classification model that can identify whether the word counts in a documentation web page are from the Statistics and Machine Learning Toolbox™ documentation. Specify to holdout 30% of the observations. Optimize the objective function using SpaRSA.
rng(1); % For reproducibility CVMdl = fitclinear(X,Ystats,'Solver','sparsa','Holdout',0.30); CMdl = CVMdl.Trained{1};
CVMdl is a ClassificationPartitionedLinear model. It contains the property Trained, which is a 1-by-1 cell array holding a ClassificationLinear model that the software trained using the training set.
Extract the training and test data from the partition definition.
trainIdx = training(CVMdl.Partition); testIdx = test(CVMdl.Partition);
Estimate the training- and test-sample edges.
eTrain = edge(CMdl,X(trainIdx,:),Ystats(trainIdx))
eTrain = 15.6660
eTest = edge(CMdl,X(testIdx,:),Ystats(testIdx))
eTest = 15.4767
One way to perform feature selection is to compare test-sample edges from multiple models. Based solely on this criterion, the classifier with the highest edge is the best classifier.
Load the NLP data set.
load nlpdataX is a sparse matrix of predictor data, and Y is a categorical vector of class labels. There are more than two classes in the data.
The models should identify whether the word counts in a web page are from the Statistics and Machine Learning Toolbox™ documentation. So, identify the labels that correspond to the Statistics and Machine Learning Toolbox™ documentation web pages. For quicker execution time, orient the predictor data so that individual observations correspond to columns.
Ystats = Y == 'stats'; X = X'; rng(1); % For reproducibility
Create a data partition which holds out 30% of the observations for testing.
Partition = cvpartition(Ystats,'Holdout',0.30); testIdx = test(Partition); % Test-set indices XTest = X(:,testIdx); YTest = Ystats(testIdx);
Partition is a cvpartition object that defines the data set partition.
Randomly choose half of the predictor variables.
p = size(X,1); % Number of predictors
idxPart = randsample(p,ceil(0.5*p));Train two binary, linear classification models: one that uses all of the predictors and one that uses half of the predictors. Optimize the objective function using SpaRSA, and indicate that observations correspond to columns.
CVMdl = fitclinear(X,Ystats,'CVPartition',Partition,'Solver','sparsa',... 'ObservationsIn','columns'); PCVMdl = fitclinear(X(idxPart,:),Ystats,'CVPartition',Partition,'Solver','sparsa',... 'ObservationsIn','columns');
CVMdl and PCVMdl are ClassificationPartitionedLinear models.
Extract the trained ClassificationLinear models from the cross-validated models.
CMdl = CVMdl.Trained{1};
PCMdl = PCVMdl.Trained{1};Estimate the test sample edge for each classifier.
fullEdge = edge(CMdl,XTest,YTest,'ObservationsIn','columns')
fullEdge = 15.4767
partEdge = edge(PCMdl,XTest(idxPart,:),YTest,'ObservationsIn','columns')
partEdge = 13.4458
Based on the test-sample edges, the classifier that uses all of the predictors is the better model.
To determine a good lasso-penalty strength for a linear classification model that uses a logistic regression learner, compare test-sample edges.
Load the NLP data set. Preprocess the data as in Feature Selection Using Test-Sample Edges.
load nlpdata Ystats = Y == 'stats'; X = X'; Partition = cvpartition(Ystats,'Holdout',0.30); testIdx = test(Partition); XTest = X(:,testIdx); YTest = Ystats(testIdx);
Create a set of 11 logarithmically-spaced regularization strengths from through .
Lambda = logspace(-8,1,11);
Train binary, linear classification models that use each of the regularization strengths. Optimize the objective function using SpaRSA. Lower the tolerance on the gradient of the objective function to 1e-8.
rng(10); % For reproducibility CVMdl = fitclinear(X,Ystats,'ObservationsIn','columns',... 'CVPartition',Partition,'Learner','logistic','Solver','sparsa',... 'Regularization','lasso','Lambda',Lambda,'GradientTolerance',1e-8)
CVMdl =
ClassificationPartitionedLinear
CrossValidatedModel: 'Linear'
ResponseName: 'Y'
NumObservations: 31572
KFold: 1
Partition: [1×1 cvpartition]
ClassNames: [0 1]
ScoreTransform: 'none'
Properties, Methods
Extract the trained linear classification model.
Mdl = CVMdl.Trained{1}Mdl =
ClassificationLinear
ResponseName: 'Y'
ClassNames: [0 1]
ScoreTransform: 'logit'
Beta: [34023×11 double]
Bias: [-11.2398 -11.2398 -11.2398 -11.2398 -11.2398 -7.1614 -5.1884 -3.7937 -3.0629 -2.9610 -2.9610]
Lambda: [1.0000e-08 7.9433e-08 6.3096e-07 5.0119e-06 3.9811e-05 3.1623e-04 0.0025 0.0200 0.1585 1.2589 10]
Learner: 'logistic'
Properties, Methods
Mdl is a ClassificationLinear model object. Because Lambda is a sequence of regularization strengths, you can think of Mdl as 11 models, one for each regularization strength in Lambda.
Estimate the test-sample edges.
e = edge(Mdl,X(:,testIdx),Ystats(testIdx),'ObservationsIn','columns')
e = 1×11
0.9986 0.9986 0.9986 0.9986 0.9986 0.9932 0.9764 0.9213 0.8277 0.8128 0.8128
Because there are 11 regularization strengths, e is a 1-by-11 vector of edges.
Plot the test-sample edges for each regularization strength. Identify the regularization strength that maximizes the edges over the grid.
figure; plot(log10(Lambda),log10(e),'-o') [~, maxEIdx] = max(e); maxLambda = Lambda(maxEIdx); hold on plot(log10(maxLambda),log10(e(maxEIdx)),'ro'); ylabel('log_{10} test-sample edge') xlabel('log_{10} Lambda') legend('Edge','Max edge') hold off
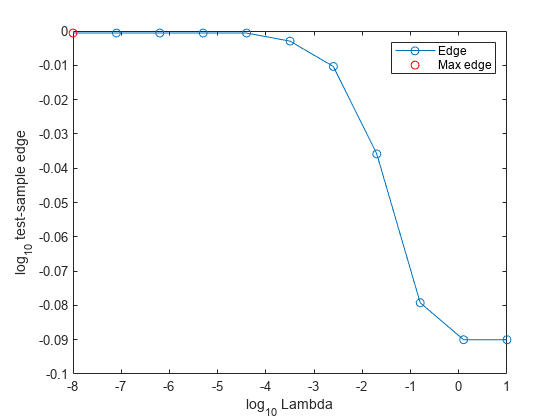
Several values of Lambda yield similarly high edges. Higher values of lambda lead to predictor variable sparsity, which is a good quality of a classifier.
Choose the regularization strength that occurs just before the edge starts decreasing.
LambdaFinal = Lambda(5);
Train a linear classification model using the entire data set and specify the regularization strength yielding the maximal edge.
MdlFinal = fitclinear(X,Ystats,'ObservationsIn','columns',... 'Learner','logistic','Solver','sparsa','Regularization','lasso',... 'Lambda',LambdaFinal);
To estimate labels for new observations, pass MdlFinal and the new data to predict.
More About
The classification edge is the weighted mean of the classification margins.
One way to choose among multiple classifiers, for example to perform feature selection, is to choose the classifier that yields the greatest edge.
The classification margin for binary classification is, for each observation, the difference between the classification score for the true class and the classification score for the false class.
The software defines the classification margin for binary classification as
x is an observation. If the true label of x is the positive class, then y is 1, and –1 otherwise. f(x) is the positive-class classification score for the observation x. The classification margin is commonly defined as m = yf(x).
If the margins are on the same scale, then they serve as a classification confidence measure. Among multiple classifiers, those that yield greater margins are better.
For linear classification models, the raw classification score for classifying the observation x, a row vector, into the positive class is defined by
For the model with regularization strength j, is the estimated column vector of coefficients (the model property
Beta(:,j)) and is the estimated, scalar bias (the model property
Bias(j)).
The raw classification score for classifying x into the negative class is –f(x). The software classifies observations into the class that yields the positive score.
If the linear classification model consists of logistic regression learners, then the
software applies the 'logit' score transformation to the raw
classification scores (see ScoreTransform).
Algorithms
By default, observation weights are prior class probabilities. If you supply weights using
Weights, then the software normalizes them to sum to the prior
probabilities in the respective classes. The software uses the normalized weights to
estimate the weighted edge.
Extended Capabilities
The
edge function supports tall arrays with the following usage
notes and limitations:
edgedoes not support talltabledata.
For more information, see Tall Arrays.
This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2016aedge fully supports GPU arrays.
If you specify a nondefault cost matrix when you train the input model object, the edge function returns a different value compared to previous releases.
The edge function uses the prior
probabilities stored in the Prior property to normalize the observation
weights of the input data. The way the function uses the Prior property
value has not changed. However, the property value stored in the input model object has changed
for a model with a nondefault cost matrix, so the function can return a different value.
For details about the property value change, see Cost property stores the user-specified cost matrix.
If you want the software to handle the cost matrix, prior
probabilities, and observation weights in the same way as in previous releases, adjust the prior
probabilities and observation weights for the nondefault cost matrix, as described in Adjust Prior Probabilities and Observation Weights for Misclassification Cost Matrix. Then, when you train a
classification model, specify the adjusted prior probabilities and observation weights by using
the Prior and Weights name-value arguments, respectively,
and use the default cost matrix.
The edge function no longer omits an observation with a
NaN score when computing the weighted mean of the classification margins. Therefore,
edge can now return NaN when the predictor data
X or the predictor variables in Tbl
contain any missing values. In most cases, if the test set observations do not contain
missing predictors, the edge function does not return
NaN.
This change improves the automatic selection of a classification model when you use
fitcauto.
Before this change, the software might select a model (expected to best classify new
data) with few non-NaN predictors.
If edge in your code returns NaN, you can update your code
to avoid this result. Remove or replace the missing values by using rmmissing or fillmissing, respectively.
The following table shows the classification models for which the
edge object function might return NaN. For more details,
see the Compatibility Considerations for each edge
function.
| Model Type | Full or Compact Model Object | edge Object Function |
|---|---|---|
| Discriminant analysis classification model | ClassificationDiscriminant, CompactClassificationDiscriminant | edge |
| Ensemble of learners for classification | ClassificationEnsemble, CompactClassificationEnsemble | edge |
| Gaussian kernel classification model | ClassificationKernel | edge |
| k-nearest neighbor classification model | ClassificationKNN | edge |
| Linear classification model | ClassificationLinear | edge |
| Neural network classification model | ClassificationNeuralNetwork, CompactClassificationNeuralNetwork | edge |
| Support vector machine (SVM) classification model | edge |
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Website auswählen
Wählen Sie eine Website aus, um übersetzte Inhalte (sofern verfügbar) sowie lokale Veranstaltungen und Angebote anzuzeigen. Auf der Grundlage Ihres Standorts empfehlen wir Ihnen die folgende Auswahl: .
Sie können auch eine Website aus der folgenden Liste auswählen:
So erhalten Sie die bestmögliche Leistung auf der Website
Wählen Sie für die bestmögliche Website-Leistung die Website für China (auf Chinesisch oder Englisch). Andere landesspezifische Websites von MathWorks sind für Besuche von Ihrem Standort aus nicht optimiert.
Amerika
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)