Resolving Issues with Nonlinearities

Nonlinearities add computational complexity, which slows down simulation. Partitions that contain nonlinearities with respect to owned states are incompatible with HDL Coder™. To use HDL Coder with networks that use the partitioning solver, you must resolve these partitions. You can use the Statistics Viewer tool to analyze the model for nonlinearities.

Remove Nonlinearities in Component Equations

Verify that your equations do not contain nonlinearities in the terms involving owned states. For example, input ･ state variable = state variable creates an unwanted nonlinearity. In this case, the model treats input as a coefficient of state variable.

This code defines the component nonlinearEquation, which uses a nonlinear equation to define a variable resistor.

component nonlinearEquation

    nodes
        p = foundation.electrical.electrical; % R:left
        n = foundation.electrical.electrical; % C:right
    end
    
    inputs
        R = {1, 'Ohm'}; % Resistance
    end
   
    variables
        v = { 0, 'V' }; % Voltage
        i = { 0, 'A' }; % Current
    end
    
    branches
        i : p.i -> n.i;
    end

    equations
        v == p.v - n.v;
        i*R == v;
    end
end

You can use this block to successfully simulate a resistor, but you are unable to generate HDL code from the model because it is nonlinear. The blocks in this model all use the default parameters.

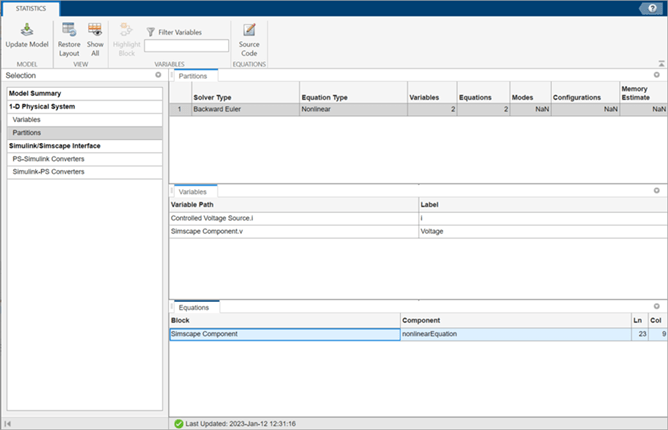
To view model statistics, in the model window, on the Debug tab, click Simscape > Statistics Viewer. Click the Update Model button to populate the current model statistics. Click Partitions under the 1-D Physical System heading. The tool shows that the equation type is Nonlinear for the electrical current variable, i. To navigate to the nonlinearity in the source code, select the Simscape Component block in the Equations tab and click Source Code.

To remove the nonlinearity, replace i*R == v with the equivalent expression, i == v/R. Now the equation is linear with respect to i, and it is suitable for HDL code generation. Click the Update Model button in the Statistics Viewer too to check that the model is linear as expected.

To learn more about terms involving owned states and connection functions, visit Understanding How the Partitioning Solver Works.

Use Simscape Physical Signal Blocks Instead of Simulink Signal Blocks

To reduce the potential for unwanted nonlinearities, use the Simscape™ physical signal manipulation blocks instead of converting Simulink^® signals. The figure shows the previous model with the nonlinear equation intact.

The figure shows the Statistics Viewer tool data. Note that equation for Partition 1 is nonlinear.

Replacing the Simulink-PS Converter block and Constant block with a PS Constant block makes the system linear. The figure shows the updated configuration.

The Statistics Viewer tool now shows that the equation type is switched linear. The figure shows the updated output.

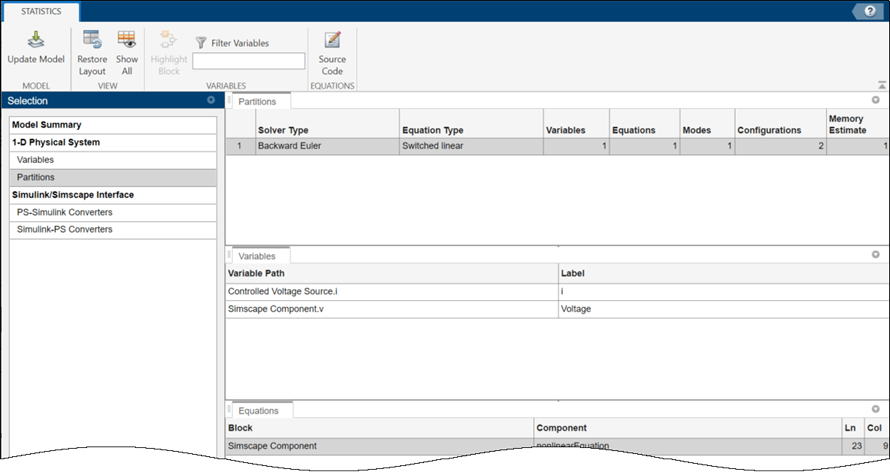
This model is suitable for HDL code generation, but it still uses the nonlinear equation, i*R == v. The partitioning solver can now convert this nonlinear equation into a switched linear system because the Resistance input is a PS Constant block. You can improve performance by converting the equation to linear. Ensure that the equation type is Linear to verify that you removed all of the nonlinearities.