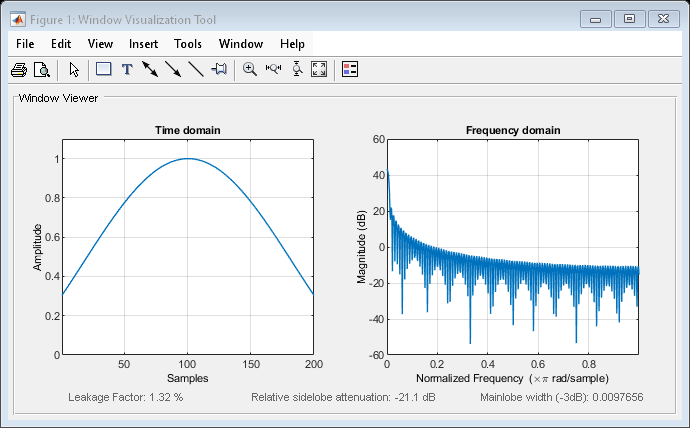
kaiser
Kaiser window
Syntax
Description
Examples
Input Arguments
Output Arguments
Algorithms
The coefficients of a Kaiser window are computed from the following equation:
where I0 is the zeroth-order modified Bessel function of the first kind. The length L = N + 1. kaiser(L,beta) is equivalent to
besseli(0,beta*sqrt(1-(((0:L-1)-(L-1)/2)/((L-1)/2)).^2))/besseli(0,beta)
To obtain a Kaiser window that represents an FIR filter with sidelobe attenuation of α dB, use the following β.
Increasing β widens the mainlobe and decreases the amplitude of the sidelobes (i.e., increases the attenuation).
References
[1] Digital Signal Processing Committee of the IEEE Acoustics, Speech, and Signal Processing Society, eds. Selected Papers in Digital Signal Processing. Vol. II. New York: IEEE Press, 1976.
[2] Kaiser, James F. "Nonrecursive Digital Filter Design Using the I0-Sinh Window Function." Proceedings of the 1974 IEEE® International Symposium on Circuits and Systems. April, 1974, pp. 20–23.
[3] Oppenheim, Alan V., and Ronald W. Schafer, with John R. Buck. Discrete-Time Signal Processing. Upper Saddle River, NJ: Prentice Hall, 1999.