instbw
Syntax
Description
ibw = instbw(___,Name=Value)FrequencyLimits=[10 20] computes the instantaneous bandwidth
of the input in the range from 10 Hz to 20 Hz.
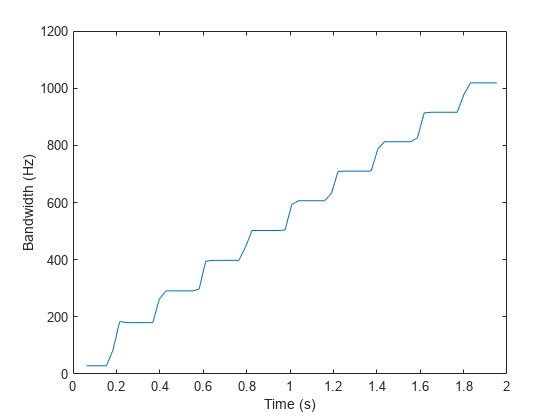
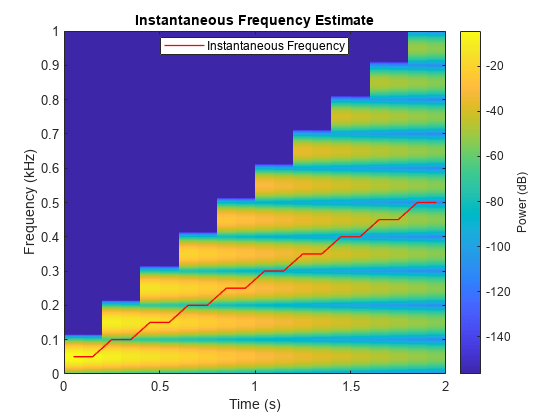
instbw(___) with no output arguments plots the
estimated instantaneous bandwidth.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
References
[1] Boashash, Boualem. “Estimating and Interpreting the Instantaneous Frequency of a Signal. I. Fundamentals.” Proceedings of the IEEE® 80, no. 4 (April 1992): 520–538. https://doi.org/10.1109/5.135376.
[2] Boashash, Boualem. "Estimating and Interpreting The Instantaneous Frequency of a Signal. II. Algorithms and Applications." Proceedings of the IEEE 80, no. 4 (May 1992): 540–568. https://doi.org/10.1109/5.135378.