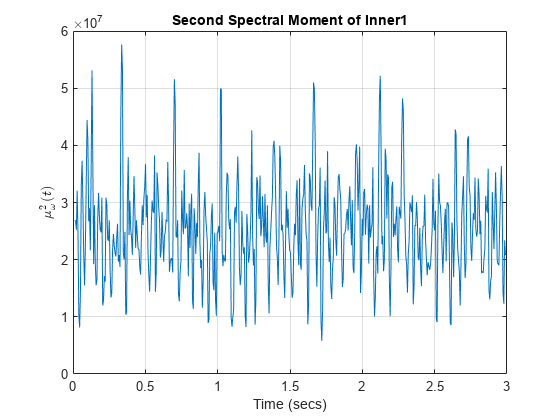
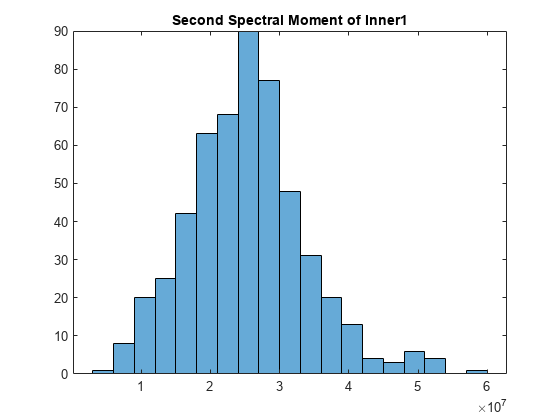
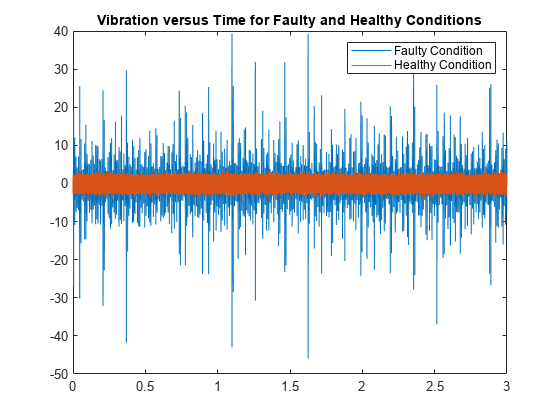
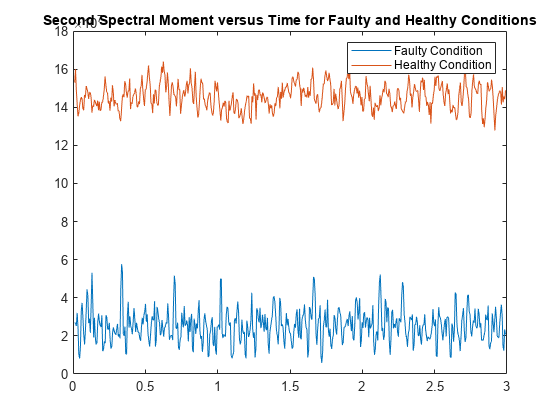
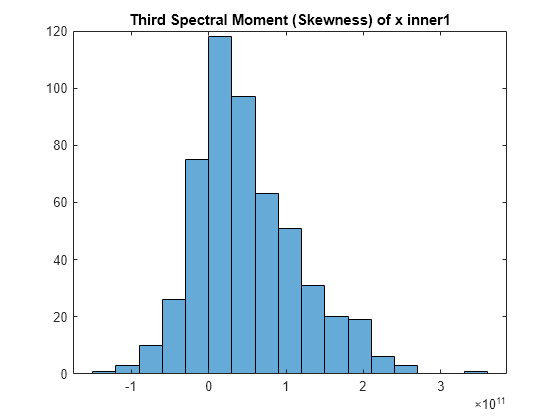
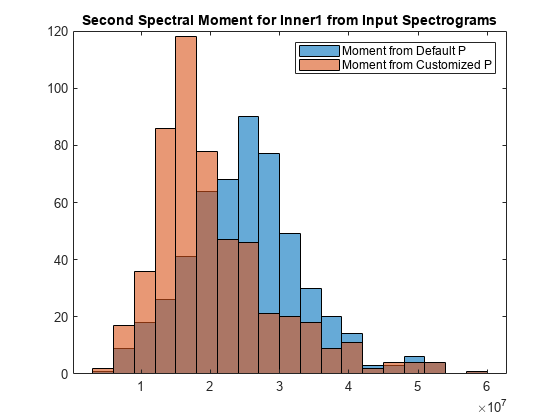
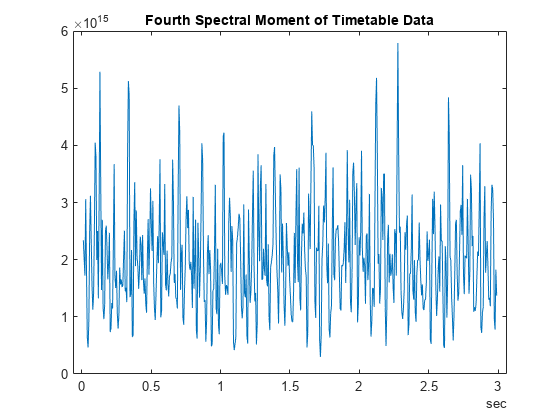
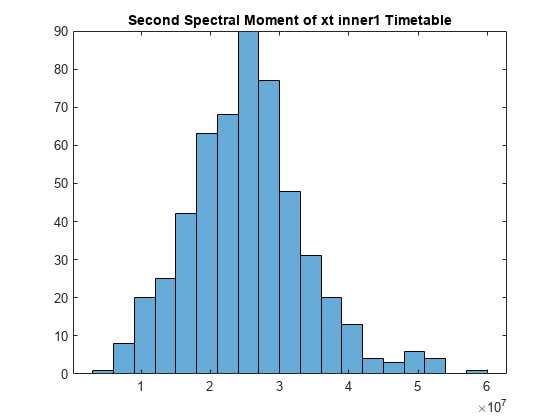
tfsmoment
Conditional spectral moment of the time-frequency distribution of a signal
Syntax
Description
Time-frequency moments provide an efficient way to characterize signals whose frequencies change in time (that is, are nonstationary). Such signals can arise from machinery with degraded or failed hardware. Classical Fourier analysis cannot capture the time-varying frequency behavior. Time-frequency distribution generated by short-time Fourier transform (STFT) or other time-frequency analysis techniques can capture the time-varying behavior, but directly treating these distributions as features carries a high computational burden, and potentially introduces unrelated and undesirable feature characteristics. In contrast, distilling the time-frequency distribution results into low-dimension time-frequency moments provides a method for capturing the essential features of the signal in a much smaller data package. Using these moments significantly reduces the computational burden for feature extraction and comparison — a key benefit for real-time operation [1], [2].
The Predictive Maintenance Toolbox™ implements the three branches of time-frequency moment:
momentS = tfsmoment(
returns the conditional spectral moment of xt,order)timetable
xt as a timetable. The
momentS variables provide the spectral moments for the
orders you specify in order. The data in
xt can be nonuniformly sampled.
momentS = tfsmoment(x,ts,order) x sampled at the time
instants specified by ts in seconds.
If
tsis a scalarduration, thentfsmomentapplies it uniformly to all samples.If
tsis a vector, thentfsmomentapplies each element to the corresponding sample inx. Use this syntax for nonuniform sampling.
momentS = tfsmoment(p,fp,tp,order) p. fp contains the frequencies
corresponding to the spectral estimate contained in p.
tp contains the vector of time instants corresponding
to the centers of the windowed segments used to compute short-time power
spectrum estimates. Use this syntax when:
You already have the power spectrum or spectrogram you want to use.
You want to customize the options for
pspectrum, rather than accept the defaultpspectrumoptions thattfsmomentapplies. Usepspectrumfirst with the options you want, and then use the outputpas input fortfsmoment. This approach also allows you to plot the power spectrogram.
momentS = tfsmoment(___,Name,Value)
You can use Name,Value with any of the input-argument
combinations in previous syntaxes.
tfsmoment(___) with no output arguments plots
the conditional spectral moment. The plot x-axis is time, and the plot y-axis is
the corresponding spectral moment.
You can use this syntax with any of the input-argument combinations in previous syntaxes.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
References
[1] Loughlin, P. J. "What Are the Time-Frequency Moments of a Signal?" Advanced Signal Processing Algorithms, Architectures, and Implementations XI, SPIE Proceedings. Vol. 4474, November 2001.
[2] Loughlin, P., F. Cakrak, and L. Cohen. "Conditional Moment Analysis of Transients with Application to Helicopter Fault Data." Mechanical Systems and Signal Processing. Vol 14, Issue 4, 2000, pp. 511–522.
Extended Capabilities
Version History
Introduced in R2018a