Signal Processing Using fgoalattain
Consider designing a linear-phase Finite Impulse Response (FIR) filter. The problem is to design a lowpass filter with magnitude one at all frequencies between 0 and 0.1 Hz and magnitude zero between 0.15 and 0.5 Hz.
The frequency response H(f) for such a filter is defined by
| (1) |
where A(f) is the magnitude
of the frequency response. One solution is to apply a goal attainment
method to the magnitude of the frequency response. Given a function
that computes the magnitude, fgoalattain will
attempt to vary the magnitude coefficients a(n)
until the magnitude response matches the desired response within some
tolerance. The function that computes the magnitude response is given
in filtmin.m. This function uses a,
the magnitude function coefficients, and w, the
discretization of the frequency domain of interest.
To
set up a goal attainment problem, you must specify the goal and weights for
the problem. For frequencies between 0 and 0.1, the goal is one. For
frequencies between 0.15 and 0.5, the goal is zero. Frequencies between
0.1 and 0.15 are not specified, so no goals or weights are needed
in this range.
This information is stored in the variable goal passed
to fgoalattain. The length of goal is
the same as the length returned by the function filtmin.
So that the goals are equally satisfied, usually weight would
be set to abs(goal). However, since some of the
goals are zero, the effect of using weight=abs(goal) will
force the objectives with weight 0 to be satisfied
as hard constraints, and the objectives with weight 1
possibly to be underattained (see Goal Attainment Method). Because all the goals are close
in magnitude, using a weight of unity for all goals
will give them equal priority. (Using abs(goal) for
the weights is more important when the magnitude of goal differs
more significantly.) Also, setting
options = optimoptions('fgoalattain','EqualityGoalCount',length(goal));
specifies that each objective should be as near as possible to its goal value (neither greater nor less than).
Step 1: Write a file filtmin.m
function y = filtmin(a,w)
n = length(a);
y = cos(w'*(0:n-1)*2*pi)*a ;Step 2: Invoke optimization routine
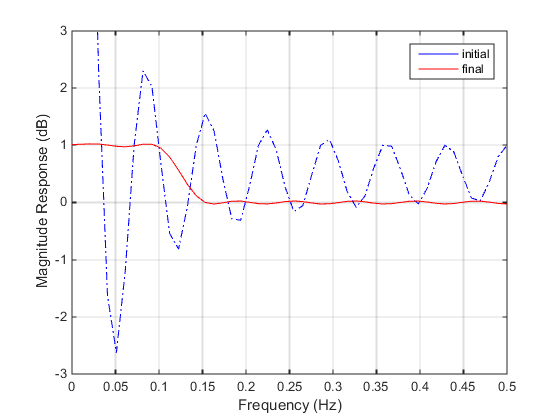
% Plot with initial coefficients a0 = ones(15,1); incr = 50; w = linspace(0,0.5,incr); y0 = filtmin(a0,w); clf, plot(w,y0,'-.b'); drawnow; % Set up the goal attainment problem w1 = linspace(0,0.1,incr) ; w2 = linspace(0.15,0.5,incr); w0 = [w1 w2]; goal = [1.0*ones(1,length(w1)) zeros(1,length(w2))]; weight = ones(size(goal)); % Call fgoalattain options = optimoptions('fgoalattain','EqualityGoalCount',length(goal)); [a,fval,attainfactor,exitflag]=fgoalattain(@(x)filtmin(x,w0),... a0,goal,weight,[],[],[],[],[],[],[],options); % Plot with the optimized (final) coefficients y = filtmin(a,w); hold on, plot(w,y,'r') axis([0 0.5 -3 3]) xlabel('Frequency (Hz)') ylabel('Magnitude Response (dB)') legend('initial', 'final') grid on
Compare the magnitude response computed with the initial coefficients
and the final coefficients (Magnitude Response with Initial and Final Magnitude Coefficients).
Note that you could use the firpm (Signal Processing Toolbox) function
in Signal Processing Toolbox™ software to design this filter.
Magnitude Response with Initial and Final Magnitude Coefficients