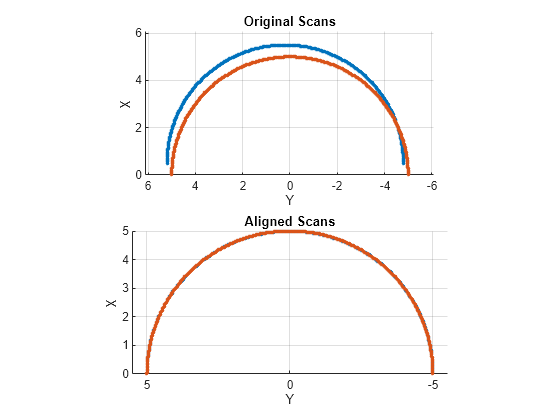
matchScans
Estimate pose between two laser scans
Syntax
Description
pose = matchScans(currRanges,currAngles,refRanges,refAngles)
[___] = matchScans(___,Name,Value)
specifies additional options specified by one or more
Name,Value pair arguments.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
References
[1] Biber, P., and W. Strasser. "The Normal Distributions Transform: A New Approach to Laser Scan Matching." Intelligent Robots and Systems Proceedings. 2003.
[2] Magnusson, Martin. "The Three-Dimensional Normal-Distributions Transform -- an Efficient Representation for Registration, Surface Analysis, and Loop Detection." PhD Dissertation. Örebro University, School of Science and Technology, 2009.
Extended Capabilities
Version History
Introduced in R2019b