Diese Seite wurde mithilfe maschineller Übersetzung übersetzt. Klicken Sie hier, um die neueste Version auf Englisch zu sehen.

accelcal

Kalibrierungsparameter für Beschleunigungsmesser

Seit R2023b

Syntax

[A,b] = accelcal(D)

[A,b] = accelcal(XUP,XDOWN,YUP,YDOWN,ZUP,ZDOWN)

[A,b] = accelcal(___,Gravity=g)

Beschreibung

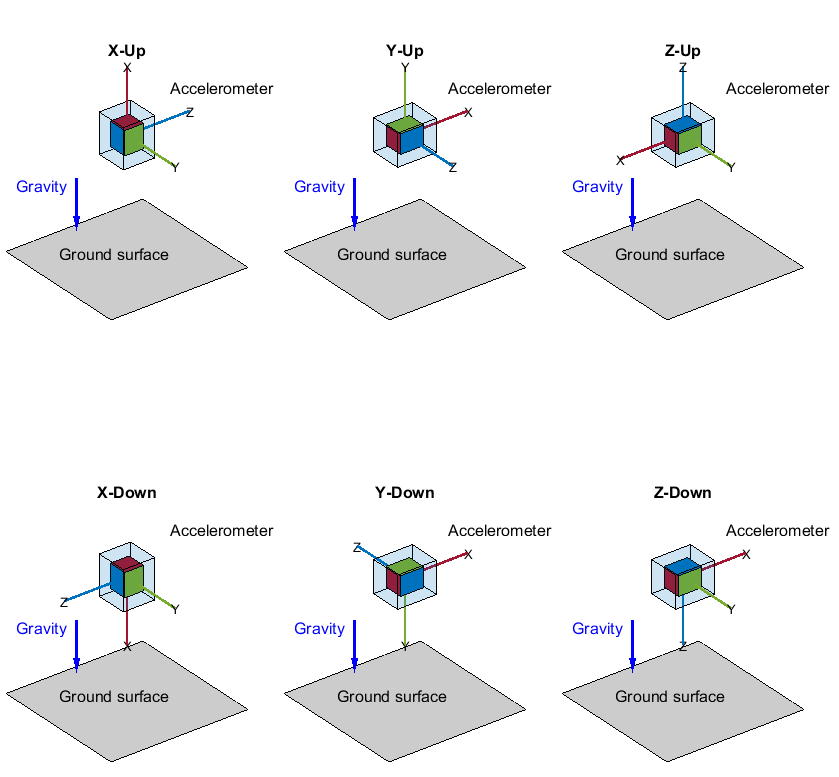
[A,b] = accelcal(D) gibt die Matrix A und den Vektor b zurück, die verwendet werden, um nicht kalibrierte Beschleunigungsmessermessungen basierend auf den Kalibrierungsdaten D zu korrigieren.

Nachdem Sie A und b ermittelt haben, ermitteln Sie die kalibrierten Daten C aus den unkalibrierten Daten U, indem Sie C = U*A + b verwenden, wobei U eine M-mal-3-Matrix ist und jede Zeile von U eine unkalibrierte Beschleunigungsmessermessung darstellt.

[A,b] = accelcal(XUP,XDOWN,YUP,YDOWN,ZUP,ZDOWN) gibt die Messdaten bei sechs Kalibrierungsorientierungen an, wie in Kalibrierungsausrichtungen für Beschleunigungsmesser dargestellt.

[A,b] = accelcal(___,Gravity=g) gibt den Wert der Erdgravitationskonstante g an.

Beispiele

Beschleunigungsmessermessungen kalibrieren

Erstellen Sie ein imuSensor-Objekt zum Generieren von Messdaten. Standardmäßig ist der Referenzrahmen des Objekts der Nord-Ost-Unten-Rahmen (NED). Geben Sie die Beschleunigungsmesserparameter so an, dass die Messungen eine konstante Abweichung und etwas zufälliges Rauschen enthalten.

accelParams =  accelparams(ConstantBias=[.1 .2 -.1],...
    NoiseDensity=1e-2*ones(1,3));
imu = imuSensor(Accelerometer=accelParams);
disp(imu.ReferenceFrame)

NED

Definieren Sie die Euler-Winkel für sechs Kalibrierungsorientierungen und konvertieren Sie sie in Quaternionen.

orients = [...
    0 90 0 % xUp
    0 0 -90 % yUp
    0 180 0 % zUp
    0 -90 0 % xDown 
    0 0 90 % yDown    
    0 0 0]; % zDown
quats = quaternion(orients,"eulerd","ZYX","frame");
N = numel(quats);

Nehmen Sie an, dass die externen Beschleunigungen und Winkelgeschwindigkeiten beide 0 sind. Simulieren Sie den IMU-Sensor, um die Kalibrierungsmessungen zu erhalten.

exAcc = zeros(N,3);
angVel = zeros(N,3);
D = imu(exAcc,angVel,quats)

D = 6×3

   -9.6490    0.2225   -0.1925
    0.0146   -9.5593    0.0153
   -0.0210    0.1928   -9.9271
    9.9363    0.1840   -0.0210
    0.0008    9.9094   -0.0655
    0.2828    0.1528    9.7232

Verwenden Sie die Funktion accelcal, um die Kalibrierungsparameter zu erhalten.

[A,b] = accelcal(D)

A = 3×3

    1.0018    0.0019   -0.0087
    0.0006    1.0078    0.0041
   -0.0154    0.0020    0.9986

b = 1×3

   -0.0956   -0.1852    0.0779

Überprüfen Sie die Kalibrierungsparameter anhand der Kalibrierungsmessungen.

DCali = D*A+b

DCali = 6×3

   -9.7587    0.0199   -0.0298
   -0.0872   -9.8187    0.0534
    0.0365   -0.0111   -9.8339
    9.8589    0.0196   -0.0284
   -0.0875    9.8012    0.0535
    0.0380   -0.0109    9.7852

Erstellen Sie einige zufällige Ausrichtungen, erhalten Sie die Beschleunigungsmessermessungen und kalibrieren Sie die Messungen.

M = 10;
randomQuats = randrot(M,1);
U = imu(zeros(M,3),zeros(M,3),randomQuats);
C = U*A+b

C = 10×3

    9.1400    3.5374   -1.3008
   -7.1185   -6.8126   -0.7088
    7.1372   -6.8065   -0.5943
   -7.9362    1.5605    5.6203
    7.4397   -2.3143   -6.2363
    7.0758   -4.0794   -5.7321
    3.1250   -5.4306    7.2655
    0.8261   -9.7286    1.3509
    0.8486    2.8606   -9.2705
   -2.4922    8.5000   -3.9532

Eingabeargumente

D — Messungen in sechs Kalibrierausrichtungen

N-mal-3-Matrix

Messungen bei den sechs Kalibrierungsausrichtungen des Beschleunigungsmessers, angegeben als N-mal-3-Matrix. N ist die Gesamtzahl der Messungen. Jede Zeile der Matrix ist eine Messung bei einer der sechs Kalibrierungsausrichtungen des Beschleunigungsmessers, wie in Kalibrierungsausrichtungen für Beschleunigungsmesser dargestellt. Um optimale Ergebnisse zu erzielen, sollte die Matrix für alle sechs Ausrichtungen eine gleiche Anzahl an Messungen enthalten.

Bei der Interpretation der Daten in D geht die Funktion standardmäßig davon aus, dass die Schwerkraftkonstante der Erde g 9,81m/s² oder 1 beträgt, je nachdem, welcher Wert näher am Mittelwert der Norm der Daten liegt.

Datentypen: single | double

XUP — Messungen bei X-Up-Ausrichtung

N₁-mal-3-Matrix

Messungen bei der x-up-Ausrichtung des Beschleunigungsmessers, angegeben als N₁-mal-3-Matrix. N₁ ist die Gesamtzahl der X-Up-Messungen. Jede Zeile der Matrix ist eine Messung des Beschleunigungsmessers. Die Definition der X-Up-Ausrichtung finden Sie im Abschnitt Kalibrierungsausrichtungen für Beschleunigungsmesser.

Datentypen: single | double

XDOWN — Messungen bei x-Down-Ausrichtung

N₂-mal-3-Matrix

Messungen bei der x-Down-Ausrichtung des Beschleunigungsmessers, angegeben als N₂-mal-3-Matrix. N₂ ist die Gesamtzahl der X-Down-Messungen. Jede Zeile der Matrix ist eine Messung des Beschleunigungsmessers. Die Definition der X-Down-Ausrichtung finden Sie im Abschnitt Kalibrierungsausrichtungen für Beschleunigungsmesser.

Datentypen: single | double

YUP — Messungen bei Y-Up-Ausrichtung

N₃-mal-3-Matrix

Messungen bei der Y-Up-Ausrichtung des Beschleunigungsmessers, angegeben als N₃-mal-3-Matrix. N₃ ist die Gesamtzahl der Y-Up-Messungen. Jede Zeile der Matrix ist eine Messung des Beschleunigungsmessers. Die Definition der Y-Up-Ausrichtung finden Sie im Abschnitt Kalibrierungsausrichtungen für Beschleunigungsmesser.

Datentypen: single | double

YDOWN — Messungen bei y-down-Ausrichtung

N₄-mal-3-Matrix

Messungen bei der Y-Down-Ausrichtung des Beschleunigungsmessers, angegeben als N₄-mal-3-Matrix. N₄ ist die Gesamtzahl der Y-Down-Messungen. Jede Zeile der Matrix ist eine Messung des Beschleunigungsmessers. Die Definition der Y-Down-Ausrichtung finden Sie im Abschnitt Kalibrierungsausrichtungen für Beschleunigungsmesser.

Datentypen: single | double

ZUP — Messungen bei Z-Up-Ausrichtung

N₅-mal-3-Matrix

Messungen bei der Z-Up-Ausrichtung des Beschleunigungsmessers, angegeben als N₅-mal-3-Matrix. N₅ ist die Gesamtzahl der Z-Up-Messungen. Jede Zeile der Matrix ist eine Messung des Beschleunigungsmessers. Die Definition der Z-Up-Ausrichtung finden Sie im Abschnitt Kalibrierungsausrichtungen für Beschleunigungsmesser.

Datentypen: single | double

ZDOWN — Messungen bei Z-Down-Ausrichtung

N₆-mal-3-Matrix

Messungen bei der Z-Down-Ausrichtung des Beschleunigungsmessers, angegeben als N₆-mal-3-Matrix. N₆ ist die Gesamtzahl der Z-Down-Messungen. Jede Zeile der Matrix ist eine Messung des Beschleunigungsmessers. Die Definition der Z-Down-Ausrichtung finden Sie im Abschnitt Kalibrierungsausrichtungen für Beschleunigungsmesser.

Datentypen: single | double

g — Erdgravitationskonstante

positiver Skalar

Schwerkraftkonstante der Erde, angegeben als positiver Skalar. Wenn Sie dieses Argument nicht angeben, geht die Funktion davon aus, dass die Schwerkraftkonstante der Erde g 9,81m/s² oder 1 beträgt, je nachdem, welcher Wert näher am Mittelwert der Norm der Daten in D liegt.

Beispiel: 9.807

Datentypen: single | double

Ausgabeargumente

A — Kalibrierungsmatrix

3x3-Matrix

Kalibrierungsmatrix, zurückgegeben als 3x3-Matrix.

Datentypen: single | double

b — Kalibrierungs-Offset-Vektor

1-mal-3-Vektor

Kalibrierungs-Offset-Vektor, zurückgegeben als 1-mal-3-Vektor.

Datentypen: single | double

Mehr über

Kalibrierungsausrichtungen für Beschleunigungsmesser

Um die Messdaten für die Kalibrierung des Beschleunigers zu erhalten, richten Sie die Ausrichtung des Beschleunigungsmesser-Messrahmens (X-Y-Z) an einer der sechs in diesem Diagramm gezeigten Ausrichtungen aus. Um beispielsweise eine X-Up-Messung zu erhalten, richten Sie die positive X-Richtung des Beschleunigermessrahmens in die entgegengesetzte Richtung der Schwerkraft aus, wie in der ersten Abbildung gezeigt.

Wenn der Beschleunigungsmesser keine Kalibrierungsfehler aufweist und sein Messrahmen wie in der Abbildung dargestellt perfekt ausgerichtet ist, können Sie in dieser Tabelle optimale Messwerte erzielen.

Orientierung	aX	aY	aZ
X-Up	-g	0	0
X-Down	+g	0	0
Y-Up	0	-g	0
Y-Down	0	+g	0
Z-Up	0	0	-g
Z-Down	0	0	+g

In der Tabelle sind a_X, a_Y und a_Z die X-, Y- und Z-Beschleunigungskomponenten. g ist die lokale Schwerkraftkonstante der Erde.

Referenzen

[1] AN4508 Application Note: Parameters and Calibration of a Low-G 3-Axis Accelerometer.

Versionsverlauf

Eingeführt in R2023b

Siehe auch

magcal | imuSensor | accelparams