odeJacobian
Description
An odeJacobian object represents the Jacobian matrix for a system
of ordinary differential equations. The Jacobian is a matrix of partial derivatives of the
functions in the system of differential equations.
Create an ode object to
represent the ODE problem, and specify an odeJacobian object as the value of
the Jacobian property to incorporate a Jacobian matrix or its sparsity
pattern into the problem.
Creation
Description
J = odeJacobianodeJacobian object with empty properties.
J = odeJacobian(PropertyName=Value)J
= odeJacobian(Jacobian=[0 1; -2 1]) specifies a constant Jacobian
matrix.
Properties
Jacobian matrix, specified as a matrix, cell array, or handle to a function that evaluates the Jacobian. The Jacobian is a matrix of partial derivatives of the functions that define the system of differential equations.
For stiff ODE solvers (ode15s, ode23s,
ode23t, and ode23tb), providing information
about the Jacobian matrix is critical for reliability and efficiency. If you do not
provide the Jacobian, then the ODE solver approximates it numerically using finite
differences.
For large systems of equations where it is not feasible to provide the entire
analytic Jacobian, use the SparsityPattern property to pass in the
sparsity pattern of the Jacobian matrix. The solver uses the sparsity pattern to
calculate a sparse Jacobian.
You can specify the Jacobian property as:
A constant matrix with calculated values for .
When
EquationTypeis"fullyimplicit", a two-element cell array with calculated values for the constant Jacobian with respect toyin the first element andypin the second element. If you specify one of the elements as[], the ODE solver approximates the corresponding Jacobian numerically while taking the provided values in the other element into account. (since R2024b)A handle to a function that computes the matrix elements and that accepts two input arguments,
dfdy = Fjac(t,y). To give the function access to parameter values in theParametersproperty, specify a third input argument in the function definition,dfdy = Fjac(t,y,p).When
EquationTypeis"fullyimplicit", a handle to a function that computes the matrix elements and that accepts three input arguments,[dfdy,dfdp] = Fjac(t,y,yp). To give the function access to parameter values in theParametersproperty, specify a fourth input argument in the function definition,[dfdy,dfdp] = Fjac(t,y,yp,p). (since R2024b)
Example: J = odeJacobian(Jacobian=@Fjac) specifies the function
Fjac that evaluates the Jacobian matrix.
Example: J = odeJacobian(Jacobian=[0 1; -2 1]) specifies a
constant Jacobian matrix.
Data Types: single | double | cell | function_handle
Jacobian sparsity pattern, specified as a sparse matrix or cell array. The sparse
matrix contains 1s where there might be nonzero entries in the
Jacobian. The ODE solver uses the sparsity pattern to generate a sparse Jacobian matrix
numerically. Use this property to improve execution time when the ODE system is large,
sparse, and you cannot provide an analytic Jacobian.
If the EquationType property of the ode object
is "fullyimplicit", specify a constant sparsity pattern as a cell
array where the first element is the sparsity pattern for the Jacobian with respect to
y and the second element is the sparsity pattern for the Jacobian
with respect to yp. If you specify one of the elements of the cell
array as [], the ODE solver approximates the corresponding Jacobian
numerically while taking the provided values in the other element into account.
Note
If you specify a Jacobian matrix using the Jacobian property,
then the solver ignores the SparsityPattern property.
Example: J = odeJacobian(SparsityPattern=S) specifies the Jacobian
sparsity pattern using sparse matrix S.
Data Types: single | double | cell (since R2024b)
Examples
The Van der Pol oscillator equation is a second-order differential equation. The equation includes a parameter , and the equation becomes stiff when the value of is large.
Using the substitutions and produces a system of two first-order equations.
The Jacobian matrix for these equations is the matrix of partial derivatives of each equation with respect to both and .
Solve the Van der Pol oscillator using and initial values of [2; 0] by creating an ode object to represent the problem.
Store the value of in the
Parametersproperty.Specify the initial values in the
InitialValueproperty.Specify the system of equations in the
ODEFcnproperty, specifying three input arguments so that the value for is passed to the function.Specify a function that calculates the Jacobian matrix in the
Jacobianproperty, specifying three input arguments so that the value for is passed to the function.
F = ode; F.Parameters = 1000; F.InitialValue = [2; 0]; F.ODEFcn = @(t,y,p) [y(2); p(1)*(1-y(1)^2)*y(2)-y(1)]; F.Jacobian = @(t,y,p) [0 1; -2*p(1)*y(1)*y(2)-1 p(1)*(1-y(1)^2)];
Display the ode object. The SelectedSolver property shows that the ode15s solver was automatically chosen for this problem.
F
F =
ode with properties:
Problem definition
ODEFcn: @(t,y,p)[y(2);p(1)*(1-y(1)^2)*y(2)-y(1)]
Parameters: 1000
InitialTime: 0
InitialValue: [2×1 double]
Jacobian: [1×1 odeJacobian]
EquationType: standard
Solver properties
AbsoluteTolerance: 1.0000e-06
RelativeTolerance: 1.0000e-03
Solver: auto
SelectedSolver: ode15s
Show all properties
Solve the system of equations over the time interval [0 3000] by using the solve method. Plot the first solution component.
S = solve(F,0,3000);
plot(S.Time,S.Solution(1,:),"-o")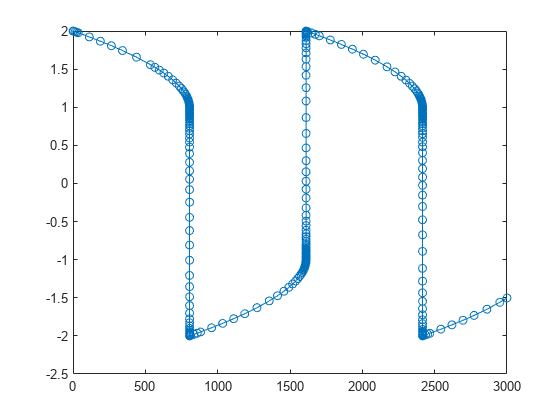
Version History
Introduced in R2023bYou can specify the Jacobian matrix Jacobian and sparsity pattern
SparsityPattern as single-precision sparse matrices. You can also
specify Jacobian as a function handle that returns single-precision
outputs.
The Jacobian property can accept functions of the form
dfdy = Fjac(t,y,yp) for implicit ODEs. Specify the ode
object property EquationType as "fullyimplicit" to
use the three-argument form for Jacobian.
If EquationType is "fullyimplicit", the
Jacobian and SparsityPattern properties also
accept a two-element cell array, where the first element corresponds to the Jacobian with
respect to y and the second element corresponds to the Jacobian with
respect to yp.
See Also
ode | odeMassMatrix | odeEvent | ODEResults | odeset
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Website auswählen
Wählen Sie eine Website aus, um übersetzte Inhalte (sofern verfügbar) sowie lokale Veranstaltungen und Angebote anzuzeigen. Auf der Grundlage Ihres Standorts empfehlen wir Ihnen die folgende Auswahl: .
Sie können auch eine Website aus der folgenden Liste auswählen:
So erhalten Sie die bestmögliche Leistung auf der Website
Wählen Sie für die bestmögliche Website-Leistung die Website für China (auf Chinesisch oder Englisch). Andere landesspezifische Websites von MathWorks sind für Besuche von Ihrem Standort aus nicht optimiert.
Amerika
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)