dissect
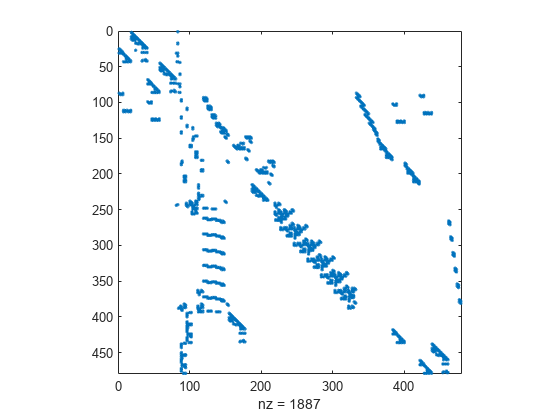
Nested dissection permutation
Description
p = dissect(A,Name,Value)dissect(A,'NumIterations',15) uses 15 refinement
iterations in the nested dissection algorithm instead of 10.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
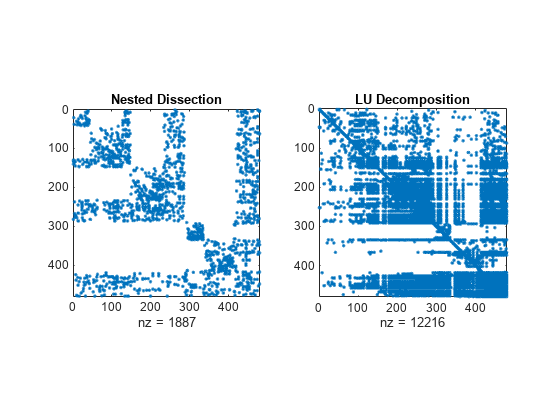
The nested dissection ordering algorithm described in [1] is a multilevel graph partitioning algorithm that is used to produce fill-reducing orderings of sparse matrices. The input matrix is treated as the adjacency matrix of a graph. The algorithm coarsens the graph by collapsing vertices and edges, reorders the smaller graph, and then uses refinement steps to uncoarsen the small graph and produce a reordering of the original graph.
The name-value pairs for dissect enable you to control various
stages of the algorithm:
Coarsening
In this phase, the algorithm creates successively smaller graphs from the original graph by collapsing together adjacent pairs of vertices.
'MaxDegreeThreshold'enables you to filter out highly connected graph vertices (which are dense columns in the matrix) by ordering them last.Partitioning
After the graph is coarsened, the algorithm completely reorders the smaller graph. At each partitioning step, the algorithm attempts to partition the graph into equal parts:
'NumSeparators'specifies how many parts to partition the graph into,'VertexWeights'optionally assigns weights to the vertices, and'MaxImbalance'specifies the threshold for the difference in weight between the different partitions.Refinement
After the smallest graph is reordered, the algorithm makes projections to enlarge the graph back to the original size by expanding the vertices that were previously combined. After each projection step, a refinement step is performed that moves vertices between partitions to improve the quality of the solution.
'NumIterations'controls how many refinement steps are used during this uncoarsening phase.
References
[1] Karypis, George and Vipin Kumar. "A Fast and High Quality Multilevel Scheme for Partitioning Irregular Graphs." SIAM Journal on Scientific Computing. Vol. 20, Number 1, 1999, pp. 359–392.
Extended Capabilities
Version History
Introduced in R2017b