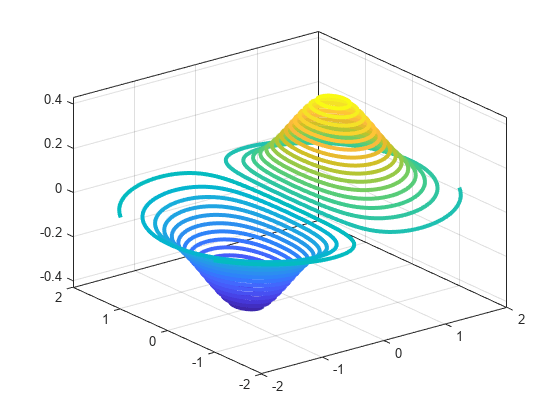
contour3
3-D contour plot
Syntax
Description
contour3( creates a 3-D contour plot
containing the isolines of matrix Z)Z, where Z
contains height values on the x-y plane. MATLAB® automatically selects the contour lines to display. The column and row indices
of Z are the x and y coordinates
in the plane, respectively.
contour3(___, specifies the
contour lines to display as the last argument in any of the previous syntaxes. Specify
levels)levels as a scalar value n to display the contour
lines at n automatically chosen levels (heights). To draw the contour
lines at specific heights, specify levels as a vector of monotonically
increasing values. To draw the contours at one height (k), specify
levels as a two-element row vector [k k].
contour3(___, specifies
the style and color of the contour lines.LineSpec)
contour3(___, specifies
additional options for the contour plot using one or more name-value pair arguments. Specify
the options after all other input arguments. For a list of properties, see Contour Properties.Name,Value)
contour3( displays the
contour plot in the target axes. Specify the axes as the first argument in any of the
previous syntaxes.ax,___)
M = contour3(___)M, which contains the (x,
y) coordinates of the vertices at each level.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Extended Capabilities
Version History
Introduced before R2006a