Replace Fitted Curve with Optimized Lookup Table
This example shows how to approximate a fitted curve or surface and generate a lookup table.
In this example, you fit a surface to two-dimensional data then use the Lookup Table Optimizer command line interface to approximate the fitted curve with a lookup table.
Fit Surface to Data
Load the data set sample_dataset, which contains data that shows the relationship between engine speed, fuel rate, and torque.
load sample_datasetTwo variables are created in the workspace. The inputs variable is two-dimensional data. The targets variable is a column vector.
Use the fit function to fit a polynomial surface to these two variables. Specify the second-degree polynomial function to fit as 'poly21'.
f = fit(inputs,targets,'poly21')f =
Linear model Poly21:
f(x,y) = p00 + p10*x + p01*y + p20*x^2 + p11*x*y
Coefficients (with 95% confidence bounds):
p00 = 1539 (599.4, 2479)
p10 = -89.93 (-126.3, -53.61)
p01 = -2.532 (-3.983, -1.08)
p20 = -0.02819 (-0.04941, -0.006961)
p11 = 0.1511 (0.09482, 0.2074)
Plot the fit and the data.
plot(f,inputs,targets)

Approximate Surface
Approximate the surface with an optimized lookup table. Create a FunctionApproximation.Problem object and specify the fitted surface curve f as the function to approximate. Set the lower and upper limits to be the range of the input values.
problem = FunctionApproximation.Problem ('f','InputLowerBounds',min(inputs),'InputUpperBounds',max(inputs))
problem =
1×1 FunctionApproximation.Problem with properties:
FunctionToApproximate: [1×1 sfit]
NumberOfInputs: 2
InputTypes: ["numerictype('double')" "numerictype('double')"]
InputLowerBounds: [14.4000 576.2000]
InputUpperBounds: [77.5000 661.5000]
OutputType: "numerictype('double')"
Options: [1×1 FunctionApproximation.Options]
You can edit the FunctionApproximation.Options object to specify additional constraints to use in the lookup table optimization process. Specify the word lengths and the maximum time to find a solution.
problem.Options.WordLengths = [8,32]; problem.Options.MaxTime = 240;
Use the solve method to create an optimized lookup table approximation. The solve method returns a FunctionApproximation.LUTSolution object.
solution = solve(problem)
ExplicitValues specification is only available for a function with 1 input dimension. Trying only even spacing. Searching for fixed-point solutions. | ID | Memory (bits) | Feasible | Table Size | Breakpoints WLs | TableData WL | BreakpointSpecification | Error(Max,Current) | | 0 | 160 | 0 | [2 2] | [8 8] | 32 | EvenSpacing | 7.812500e-03, 2.841326e+01 | | 1 | 672 | 0 | [4 5] | [8 8] | 32 | EvenSpacing | 7.812500e-03, 9.828165e+01 | | 2 | 512 | 0 | [3 5] | [8 8] | 32 | EvenSpacing | 7.812500e-03, 1.347941e+02 | | 3 | 544 | 0 | [4 4] | [8 8] | 32 | EvenSpacing | 7.812500e-03, 1.282285e+02 | | 4 | 416 | 0 | [3 4] | [8 8] | 32 | EvenSpacing | 7.812500e-03, 1.364575e+02 | | 5 | 1824 | 0 | [7 8] | [8 8] | 32 | EvenSpacing | 7.812500e-03, 5.546356e+01 | | 6 | 1568 | 0 | [6 8] | [8 8] | 32 | EvenSpacing | 7.812500e-03, 5.816418e+01 | | 7 | 5024 | 0 | [13 12] | [8 8] | 32 | EvenSpacing | 7.812500e-03, 5.507808e+01 | | 8 | 4640 | 0 | [12 12] | [8 8] | 32 | EvenSpacing | 7.812500e-03, 5.214569e+01 | | 9 | 19168 | 0 | [26 23] | [8 8] | 32 | EvenSpacing | 7.812500e-03, 2.238620e+01 | | 10 | 16224 | 0 | [22 23] | [8 8] | 32 | EvenSpacing | 7.812500e-03, 1.908110e+01 | | 11 | 31680 | 0 | [43 23] | [8 8] | 32 | EvenSpacing | 7.812500e-03, 1.908110e+01 | | 12 | 94240 | 1 | [128 23] | [8 8] | 32 | EvenSpacing | 7.812500e-03, 1.761679e-03 | | 13 | 47136 | 0 | [64 23] | [8 8] | 32 | EvenSpacing | 7.812500e-03, 1.908110e+01 | | 14 | 2080 | 0 | [8 8] | [8 8] | 32 | EvenSpacing | 7.812500e-03, 5.546356e+01 | | 15 | 5792 | 0 | [15 12] | [8 8] | 32 | EvenSpacing | 7.812500e-03, 3.727233e+01 | | 16 | 23584 | 0 | [32 23] | [8 8] | 32 | EvenSpacing | 7.812500e-03, 2.567721e+01 | | 17 | 4256 | 0 | [11 12] | [8 8] | 32 | EvenSpacing | 7.812500e-03, 5.507808e+01 | | 18 | 3872 | 0 | [10 12] | [8 8] | 32 | EvenSpacing | 7.812500e-03, 3.727233e+01 | | 19 | 14016 | 0 | [19 23] | [8 8] | 32 | EvenSpacing | 7.812500e-03, 1.908110e+01 | | 20 | 49184 | 1 | [128 12] | [8 8] | 32 | EvenSpacing | 7.812500e-03, 1.761679e-03 | | 21 | 24608 | 0 | [128 6] | [8 8] | 32 | EvenSpacing | 7.812500e-03, 4.749187e+01 | | 22 | 32800 | 0 | [128 8] | [8 8] | 32 | EvenSpacing | 7.812500e-03, 1.107267e+01 | | 23 | 256 | 0 | [2 2] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 2.805641e+01 | | 24 | 768 | 0 | [4 5] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 9.748046e+01 | | 25 | 608 | 0 | [3 5] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 7.014101e+00 | | 26 | 640 | 0 | [4 4] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 1.295056e+02 | | 27 | 512 | 0 | [3 4] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 7.014101e+00 | | 28 | 2144 | 0 | [7 9] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 4.835884e+01 | | 29 | 1856 | 0 | [6 9] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 5.643476e+01 | | 30 | 1920 | 0 | [7 8] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 5.542954e+01 | | 31 | 1664 | 0 | [6 8] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 5.643476e+01 | | 32 | 7200 | 0 | [13 17] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 2.410273e+01 | | 33 | 6656 | 0 | [12 17] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 2.571471e+01 | | 34 | 6784 | 0 | [13 16] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 2.585440e+01 | | 35 | 6272 | 0 | [12 16] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 2.585440e+01 | | 36 | 26528 | 0 | [25 33] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 1.191428e+01 | | 37 | 25472 | 0 | [24 33] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 1.234469e+01 | | 38 | 25728 | 0 | [25 32] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 1.221390e+01 | | 39 | 24704 | 0 | [24 32] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 1.234470e+01 | | 40 | 14240 | 0 | [21 21] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 1.402265e+01 | | 41 | 28928 | 0 | [30 30] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 1.325468e+01 | | 42 | 37120 | 0 | [34 34] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 1.141255e+01 | | 43 | 41600 | 0 | [36 36] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 1.093924e+01 | | 44 | 43936 | 0 | [37 37] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 1.081053e+01 | | 45 | 46336 | 0 | [38 38] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 1.049341e+01 | | 46 | 2432 | 0 | [8 9] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 4.835884e+01 | | 47 | 2176 | 0 | [8 8] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 5.542954e+01 | | 48 | 8288 | 0 | [15 17] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 2.410273e+01 | | 49 | 7744 | 0 | [14 17] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 2.410273e+01 | | 50 | 7808 | 0 | [15 16] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 2.585440e+01 | | 51 | 7296 | 0 | [14 16] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 2.585439e+01 | | 52 | 30752 | 0 | [29 33] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 1.191428e+01 | | 53 | 29696 | 0 | [28 33] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 1.191428e+01 | | 54 | 29824 | 0 | [29 32] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 1.221390e+01 | | 55 | 28800 | 0 | [28 32] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 1.221390e+01 | | 56 | 39328 | 0 | [35 35] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 1.136963e+01 | | 57 | 4352 | 0 | [11 12] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 2.848471e+01 | | 58 | 3968 | 0 | [10 12] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 3.514238e+01 | | 59 | 4000 | 0 | [11 11] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 2.848471e+01 | | 60 | 3648 | 0 | [10 11] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 3.884241e+01 | | 61 | 15584 | 0 | [21 23] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 1.402265e+01 | | 62 | 14848 | 0 | [20 23] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 1.755374e+01 | | 63 | 14912 | 0 | [21 22] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 1.402265e+01 | | 64 | 14208 | 0 | [20 22] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 1.854448e+01 | | 65 | 6848 | 0 | [14 15] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 2.787487e+01 | | 66 | 6368 | 0 | [13 15] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 2.787487e+01 | | 67 | 26912 | 0 | [27 31] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 1.286638e+01 | | 68 | 25920 | 0 | [26 31] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 1.286638e+01 | | 69 | 26048 | 0 | [27 30] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 1.325468e+01 | | 70 | 25088 | 0 | [26 30] | [32 32] | 32 | EvenSpacing | 7.812500e-03, 1.325468e+01 | | 71 | 208 | 0 | [2 2] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 2.805641e+01 | | 72 | 720 | 0 | [4 5] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 9.853785e+01 | | 73 | 560 | 0 | [3 5] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 1.350093e+02 | | 74 | 592 | 0 | [4 4] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 1.277248e+02 | | 75 | 464 | 0 | [3 4] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 1.364309e+02 | | 76 | 1872 | 0 | [7 8] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 5.450379e+01 | | 77 | 1616 | 0 | [6 8] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 5.590166e+01 | | 78 | 5072 | 0 | [13 12] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 3.631948e+01 | | 79 | 4688 | 0 | [12 12] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 3.631948e+01 | | 80 | 18480 | 0 | [25 23] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 1.808342e+01 | | 81 | 17744 | 0 | [24 23] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 1.808342e+01 | | 82 | 36144 | 0 | [49 23] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 1.808342e+01 | | 83 | 35408 | 0 | [48 23] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 1.808342e+01 | | 84 | 26576 | 0 | [36 23] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 1.808342e+01 | | 85 | 27312 | 0 | [37 23] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 1.808342e+01 | | 86 | 28048 | 0 | [38 23] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 1.808342e+01 | | 87 | 2128 | 0 | [8 8] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 5.450379e+01 | | 88 | 5840 | 0 | [15 12] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 3.631948e+01 | | 89 | 5456 | 0 | [14 12] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 3.631948e+01 | | 90 | 21424 | 0 | [29 23] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 1.808342e+01 | | 91 | 20688 | 0 | [28 23] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 1.808342e+01 | | 92 | 42032 | 0 | [57 23] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 1.808342e+01 | | 93 | 41296 | 0 | [56 23] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 1.808342e+01 | | 94 | 4304 | 0 | [11 12] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 2.805640e-01 | | 95 | 3920 | 0 | [10 12] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 3.631948e+01 | | 96 | 15536 | 0 | [21 23] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 7.014104e-02 | | 97 | 14800 | 0 | [20 23] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 1.808342e+01 | | 98 | 30256 | 0 | [41 23] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 1.808342e+01 | | 99 | 29520 | 0 | [40 23] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 1.808342e+01 | | 100 | 22160 | 0 | [30 23] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 1.808342e+01 | | 101 | 25104 | 0 | [34 23] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 1.808342e+01 | | 102 | 19952 | 0 | [27 23] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 1.808342e+01 | | 103 | 19216 | 0 | [26 23] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 1.808342e+01 | | 104 | 39088 | 0 | [53 23] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 1.808342e+01 | | 105 | 38352 | 0 | [52 23] | [32 8] | 32 | EvenSpacing | 7.812500e-03, 1.808342e+01 | | 106 | 160 | 0 | [2 2] | [8 8] | 32 | EvenPow2Spacing | 7.812500e-03, 2.977238e+02 | | 107 | 800 | 0 | [4 6] | [8 8] | 32 | EvenPow2Spacing | 7.812500e-03, 1.394755e+02 | | 108 | 416 | 0 | [4 3] | [8 8] | 32 | EvenPow2Spacing | 7.812500e-03, 2.378911e+02 | | 109 | 1568 | 0 | [8 6] | [8 8] | 32 | EvenPow2Spacing | 7.812500e-03, 1.059496e+02 | | 110 | 6176 | 0 | [16 12] | [8 8] | 32 | EvenPow2Spacing | 7.812500e-03, 5.507808e+01 | | 111 | 23584 | 0 | [32 23] | [8 8] | 32 | EvenPow2Spacing | 7.812500e-03, 2.567721e+01 | | 112 | 47136 | 0 | [64 23] | [8 8] | 32 | EvenPow2Spacing | 7.812500e-03, 1.908110e+01 | | 113 | 3104 | 0 | [8 12] | [8 8] | 32 | EvenPow2Spacing | 7.812500e-03, 7.802988e+01 | | 114 | 11808 | 0 | [16 23] | [8 8] | 32 | EvenPow2Spacing | 7.812500e-03, 3.870031e+01 | Searching for floating-point solutions. Time limit for finding a solution has been reached. Best Solution | ID | Memory (bits) | Feasible | Table Size | Breakpoints WLs | TableData WL | BreakpointSpecification | Error(Max,Current) | | 20 | 49184 | 1 | [128 12] | [8 8] | 32 | EvenSpacing | 7.812500e-03, 1.761679e-03 |
solution =
1×1 FunctionApproximation.LUTSolution with properties:
ID: 20
Feasible: "true"
View the lookup table data.
solution.TableData
ans = struct with fields:
BreakpointValues: {[1×128 double] [576 584 592 600 608 616 624 632 640 648 656 664]}
BreakpointDataTypes: [1×2 embedded.numerictype]
TableValues: [128×12 double]
TableDataType: [1×1 embedded.numerictype]
IsEvenSpacing: 1
Interpolation: Linear
Compare Lookup Table Approximation to Original Function
Compare the numerical behavior of the original surface fit function with the optimized lookup table approximation.
compare(solution)
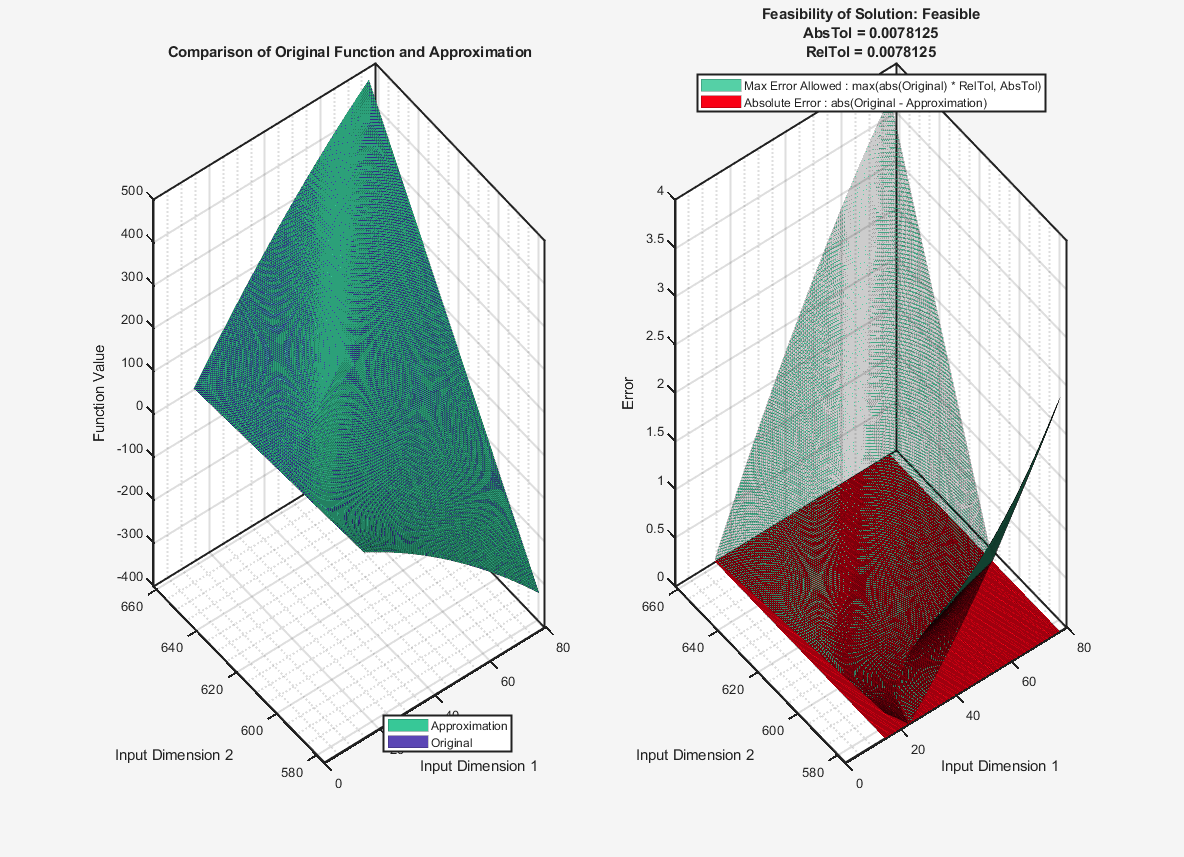
ans=1×2 struct array with fields:
Breakpoints
Original
Approximate
Generate Subsystem
Use the approximate method to generate a Simulink® subsystem that contains the lookup table approximation.
approximate(solution)
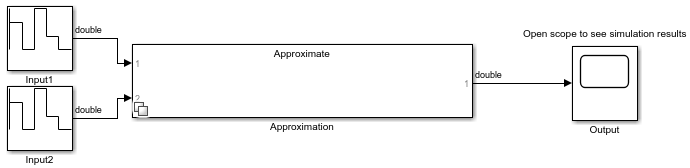
See Also
fit (Curve Fitting Toolbox) | FunctionApproximation.Problem | FunctionApproximation.Options
Topics
- Optimize Lookup Tables for Memory-Efficiency Programmatically
- Parametric Fitting (Curve Fitting Toolbox)