spreadbyfd
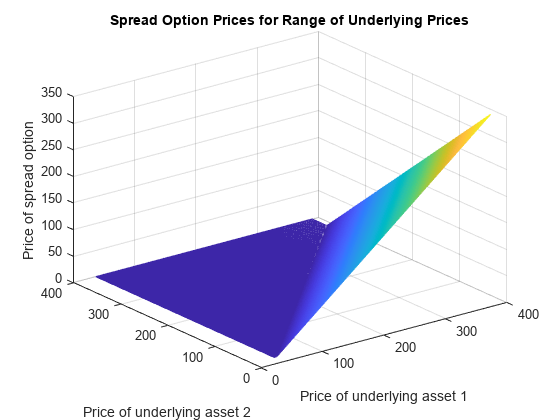
Price European or American spread options using finite difference method
Syntax
Description
Price = spreadbyfd(RateSpec,StockSpec1,StockSpec2,Settle,Maturity,OptSpec,Strike,Corr)StockSpec1 minus the asset defined in
StockSpec2.
Price = spreadbyfd(___,Name,Value)
[
returns the Price,PriceGrid,AssetPrice1,AssetPrice2,Times]
= spreadbyfd(RateSpec,StockSpec1,StockSpec2,Settle,Maturity,OptSpec,Strike,Corr)Price, PriceGrid,
AssetPrice1, AssetPrice2, and
Times for a European or American call or put spread options using the
Alternate Direction Implicit (ADI) finite difference method. The spread is between the
asset defined in StockSpec1 minus the asset defined in
StockSpec2.
[ returns the
Price,PriceGrid,AssetPrice1,AssetPrice2,Times]
= spreadbyfd(___,Name,Value)Price, PriceGrid, AssetPrice1,
AssetPrice2, and Times and adds optional
name-value pair arguments.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
References
[1] Carmona, R., Durrleman, V. “Pricing and Hedging Spread Options.” SIAM Review. Vol. 45, No. 4, pp. 627–685, Society for Industrial and Applied Mathematics, 2003.
[2] Villeneuve, S., Zanette, A. “Parabolic ADI Methods for Pricing American Options on Two Stocks.” Mathematics of Operations Research. Vol. 27, No. 1, pp. 121–149, INFORMS, 2002.
[3] Ikonen, S., Toivanen, J. Efficient Numerical Methods for Pricing American Options Under Stochastic Volatility. Wiley InterScience, 2007.