FixedBond
FixedBond instrument object
Description
Create and price a FixedBond instrument object for one of
more Fixed Bond instruments using this workflow:
Use
fininstrumentto create aFixedBondinstrument object for one of more Fixed Bond instruments.Use
ratecurveto specify a curve model for theFixedBondinstrument object or use aHullWhite,BlackKarasinski,BlackDermanToy,BraceGatarekMusiela,SABRBraceGatarekMusiela,CoxIngersollRoss, orLinearGaussian2Fmodel.Choose a pricing method.
When using a
ratecurveusefinpricerto specify aDiscountpricing method for one or moreFixedBondinstruments.When using a
HullWhite,BlackKarasinski,CoxIngersollRoss, orBlackDermanToymodel, usefinpricerto specify anIRTreepricing method for one or moreFixedBondinstruments.When using a
HullWhite,BlackKarasinski,BraceGatarekMusiela,SABRBraceGatarekMusiela, orLinearGaussian2Fmodel, usefinpricerto specify anIRMonteCarlopricing method for one or moreFixedBondinstruments.
For more detailed information on this workflow, see Get Started with Workflows Using Object-Based Framework for Pricing Financial Instruments.
For more information on the available models and pricing methods for a
FixedBond instrument, see Choose Instruments, Models, and Pricers.
Creation
Syntax
Description
FixedBondObj = fininstrument(InstrumentType,'CouponRate',couponrate_value,'Maturity',maturity_date)FixedBond object for one of more Fixed Bond
instruments by specifying InstrumentType and sets the
properties for the
required name-value pair arguments CouponRate and
Maturity.
The FixedBond instrument supports a vanilla bond, a
stepped coupon bond, and an amortizing bond. For more information, see More About.
FixedBondObj = fininstrument(___,Name,Value)FixedBondObj =
fininstrument("FixedBond",'CouponRate',0.34,'Maturity',datetime(2019,1,30),'Period',4,'Basis',1,'Principal',100,'FirstCouponDate',datetime(2016,1,30),'EndMonthRule',true,'Name',"fixedbond_instrument")
creates a FixedBond option with a coupon rate of 0.34 and
a maturity of January 30, 2019. You can specify multiple name-value pair
arguments.
Input Arguments
Instrument type, specified as a string with the value of
"FixedBond", a character vector with the value of
'FixedBond', an
NINST-by-1 string array with
values of "FixedBond", or an
NINST-by-1 cell array of
character vectors with values of 'FixedBond'.
Data Types: char | cell | string
Name-Value Arguments
Specify required
and optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where
Name is the argument name and Value is
the corresponding value. Name-value arguments must appear after other arguments,
but the order of the pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: FixedBondObj =
fininstrument("FixedBond",'CouponRate',0.34,'Maturity',datetime(2019,1,30),'Period',4,'Basis',1,'Principal',100,'FirstCouponDate',datetime(2016,1,30),'EndMonthRule',true,'Name',"fixedbond_instrument")
Required FixedBond Name-Value Pair Arguments
FixedBond coupon rate, specified as the
comma-separated pair consisting of 'CouponRate'
and a scalar decimal or an
NINST-by-1 vector of
decimals for an annual rate or a timetable where the first column is
dates and the second column is associated rates. The date indicates
the last day that the coupon rate is valid.
Note
If you are creating one or more FixedBond
instruments and use a timetable, the timetable specification
applies to all of the FixedBond instruments.
CouponRate does not accept an
NINST-by-1 cell array
of timetables as input.
Data Types: double | timetable
FixedBond maturity date, specified as the
comma-separated pair consisting of 'Maturity' and
a scalar or an NINST-by-1
vector using a datetime array, string array, or date character
vectors.
To support existing code, FixedBond also
accepts serial date numbers as inputs, but they are not recommended.
If you use date character vectors or strings, the format must be
recognizable by datetime because
the Maturity property is stored as a
datetime.
Optional FixedBond Name-Value Pair Arguments
Frequency of payments, specified as the comma-separated pair
consisting of 'Period' and a scalar integer or an
NINST-by-1 vector of
integers. Values for Period are
1, 2,
3, 4, 6, or
12.
Data Types: double
Day count basis, specified as the comma-separated pair consisting
of 'Basis' and scalar integer or an
NINST-by-1 vector of
integers using the following values:
0 — actual/actual
1 — 30/360 (SIA)
2 — actual/360
3 — actual/365
4 — 30/360 (PSA)
5 — 30/360 (ISDA)
6 — 30/360 (European)
7 — actual/365 (Japanese)
8 — actual/actual (ICMA)
9 — actual/360 (ICMA)
10 — actual/365 (ICMA)
11 — 30/360E (ICMA)
12 — actual/365 (ISDA)
13 — BUS/252
For more information, see Basis.
Data Types: double
Principal amount or principal value schedule, specified as the
comma-separated pair consisting of 'Principal'
and a scalar numeric or an
NINST-by-1 numeric vector
or a timetable.
Principal accepts a timetable, where the
first column is dates and the second column is the associated
notional principal value. The date indicates the last day that the
principal value is valid.
Note
If you are creating one or more FixedBond
instruments and use a timetable, the timetable specification
applies to all of the FixedBond instruments.
Principal does not accept an
NINST-by-1 cell array
of timetables as input.
Data Types: double | timetable
Flag indicating whether cash flow is adjusted by day count
convention, specified as the comma-separated pair consisting of
'DaycountAdjustedCashFlow' and a scalar
logical or an NINST-by-1
vector of logicals with values of true or
false.
Data Types: logical
Business day conventions for cash flow dates, specified as the
comma-separated pair consisting of
'BusinessDayConvention' and a scalar string
or character vector or an
NINST-by-1 cell array of
character vectors or string array. The selection for business day
convention determines how nonbusiness days are treated. Nonbusiness
days are defined as weekends plus any other date that businesses are
not open (for example, statutory holidays). Values are:
"actual"— Nonbusiness days are effectively ignored. Cash flows that fall on nonbusiness days are assumed to be distributed on the actual date."follow"— Cash flows that fall on a nonbusiness day are assumed to be distributed on the following business day."modifiedfollow"— Cash flows that fall on a nonbusiness day are assumed to be distributed on the following business day. However, if the following business day is in a different month, the previous business day is adopted instead."previous"— Cash flows that fall on a nonbusiness day are assumed to be distributed on the previous business day."modifiedprevious"— Cash flows that fall on a nonbusiness day are assumed to be distributed on the previous business day. However, if the previous business day is in a different month, the following business day is adopted instead.
Data Types: char | cell | string
Holidays used in computing business days, specified as the
comma-separated pair consisting of 'Holidays' and
dates using an NINST-by-1
vector of a datetime array, string array, or date character vectors.
For
example:
H = holidays(datetime('today'),datetime(2025,12,15)); FixedBondObj = fininstrument("FixedBond",'CouponRate',0.34,'Maturity',datetime(2025,12,15),'Holidays',H)
To support existing code, FixedBond also
accepts serial date numbers as inputs, but they are not recommended.
End-of-month rule flag for generating dates when
Maturity is an end-of-month date for a month
with 30 or fewer days, specified as the comma-separated pair
consisting of 'EndMonthRule' and a scalar logical
value or an NINST-by-1 vector
of logicals with values of true or
false.
If you set
EndMonthRuletofalse, the software ignores the rule, meaning that a payment date is always the same numerical day of the month.If you set
EndMonthRuletotrue, the software sets the rule on, meaning that a payment date is always the last actual day of the month.
Data Types: logical
Bond issue date, specified as the comma-separated pair consisting
of 'IssueDate' and a scalar or an
NINST-by-1 vector using a
datetime array, string array, or date character vectors.
To support existing code, FixedBond also
accepts serial date numbers as inputs, but they are not recommended.
If you use date character vectors or strings, the format must be
recognizable by datetime because
the IssueDate property is stored as a
datetime.
Irregular first coupon date, specified as the comma-separated pair
consisting of 'FirstCouponDate' and a scalar or
an NINST-by-1 vector using a
datetime array, string array, or date character vectors.
To support existing code, FixedBond also
accepts serial date numbers as inputs, but they are not recommended.
When FirstCouponDate and
LastCouponDate are both specified,
FirstCouponDate takes precedence in
determining the coupon payment structure. If you do not specify
FirstCouponDate, the cash flow payment dates
are determined from other inputs.
If you use date character vectors or strings, the format must be
recognizable by datetime because
the FirstCouponDate property is stored as a
datetime.
Irregular last coupon date, specified as the comma-separated pair
consisting of 'LastCouponDate' and a scalar or an
NINST-by-1 vector using a
datetime array, string array, or date character vectors.
To support existing code, FixedBond also
accepts serial date numbers as inputs, but they are not recommended.
If you specify LastCouponDate but not
FirstCouponDate,
LastCouponDate determines the coupon
structure of the bond. The coupon structure of a bond is truncated
at LastCouponDate, regardless of where it falls,
and is followed only by the bond's maturity cash flow date. If you
do not specify LastCouponDate, the cash flow
payment dates are determined from other inputs.
If you use date character vectors or strings, the format must be
recognizable by datetime because
the LastCouponDate property is stored as a
datetime.
Forward starting date of payments, specified as the
comma-separated pair consisting of 'StartDate'
and a scalar or an NINST-by-1
vector using a datetime array, string array, or date character
vectors.
To support existing code, FixedBond also
accepts serial date numbers as inputs, but they are not recommended.
If you use date character vectors or strings, the format must be
recognizable by datetime because
the StartDate property is stored as a
datetime.
User-defined name for one of more instruments, specified as the
comma-separated pair consisting of 'Name' and a
scalar string or character vector or an
NINST-by-1 cell array of
character vectors or string array.
Data Types: char | cell | string
Output Arguments
Fixed Bond instrument, returned as a FixedBond
object.
Properties
FixedBond coupon annual rate, returned as a scalar
decimal or an NINST-by-1 vector of
decimals or a timetable.
Data Types: double | timetable
FixedBond maturity date, returned as a scalar datetime
or NINST-by-1 vector of
datetimes.
Data Types: datetime
Frequency of payments per year, returned as a scalar integer or an
NINST-by-1 vector of
integers.
Data Types: double
Day count basis, returned as a scalar integer or an
NINST-by-1 vector of integers.
Data Types: double
Principal amount or principal value schedules, returned as a scalar
numeric or an NINST-by-1 numeric
vector or a timetable.
Data Types: double
Flag indicating whether cash flow adjusts for day count convention,
returned as scalar logical or an
NINST-by-1 vector of logicals with
values of true or false.
Data Types: logical
Business day conventions, returned as a scalar string or an
NINST-by-1 string array.
Data Types: string
Holidays used in computing business days, returned as an
NINST-by-1 vector of
datetimes.
Data Types: datetime
End-of-month rule flag for generating dates when
Maturity is an end-of-month date for a month having
30 or fewer days, returned as a scalar logical or an
NINST-by-1 vector of logical
values.
Data Types: logical
Bond issue date, returned as a scalar datetime or an
NINST-by-1 vector of
datetimes.
Data Types: datetime
Irregular first coupon date, returned as a scalar datetime or an
NINST-by-1 vector of datetimes.
Data Types: datetime
Irregular last coupon date, returned as a scalar datetime or an
NINST-by-1 vector of
datetimes.
Data Types: datetime
Forward starting date of payments, returned as a scalar datetime or an
NINST-by-1 vector of datetimes.
Data Types: datetime
User-defined name for the instrument, returned as a scalar string or an
NINST-by-1 string array.
Data Types: string
Object Functions
cashflows | Compute cash flow for FixedBond, FloatBond,
Swap, FRA, STIRFuture,
OISFuture, OvernightIndexedSwap, or
Deposit instrument |
Examples
This example shows the workflow to price a vanilla FixedBond instrument when you use a ratecurve and a Discount pricing method.
Create FixedBond Instrument Object
Use fininstrument to create a FixedBond instrument object.
FixB = fininstrument("FixedBond",'Maturity',datetime(2022,9,15),'CouponRate',0.021,'Period',2,'Basis',1,'Principal',100,'Name',"fixed_bond_instrument")
FixB =
FixedBond with properties:
CouponRate: 0.0210
Period: 2
Basis: 1
EndMonthRule: 1
Principal: 100
DaycountAdjustedCashFlow: 0
BusinessDayConvention: "actual"
Holidays: NaT
IssueDate: NaT
FirstCouponDate: NaT
LastCouponDate: NaT
StartDate: NaT
Maturity: 15-Sep-2022
Name: "fixed_bond_instrument"
Create ratecurve Object
Create a ratecurve object using ratecurve.
Settle = datetime(2018,9,15); Type = 'zero'; ZeroTimes = [calmonths(6) calyears([1 2 3 4 5 7 10 20 30])]'; ZeroRates = [0.0052 0.0055 0.0061 0.0073 0.0094 0.0119 0.0168 0.0222 0.0293 0.0307]'; ZeroDates = Settle + ZeroTimes; myRC = ratecurve('zero',Settle,ZeroDates,ZeroRates)
myRC =
ratecurve with properties:
Type: "zero"
Compounding: -1
Basis: 0
Dates: [10×1 datetime]
Rates: [10×1 double]
Settle: 15-Sep-2018
InterpMethod: "linear"
ShortExtrapMethod: "next"
LongExtrapMethod: "previous"
Create Discount Pricer Object
Use finpricer to create a Discount pricer object and use the ratecurve object with the 'DiscountCurve' name-value pair argument.
outPricer = finpricer("Discount",'DiscountCurve',myRC)
outPricer =
Discount with properties:
DiscountCurve: [1×1 ratecurve]
Price FixedBond Instrument
Use price to compute the price and sensitivities for the FixedBond instrument.
[Price, outPR] = price(outPricer, FixB,["all"])Price = 104.5679
outPR =
priceresult with properties:
Results: [1×2 table]
PricerData: []
outPR.Results
ans=1×2 table
Price DV01
______ ________
104.57 0.040397
This example shows how to create a FixedBond instrument and then use any of the following Financial Toolbox™ functions to perform bond analytics: bnddurp, bnddury, bndconvp, bndconvy, bndkrdur, cfdur, and cfconv.
Create FixedBond Instrument Object
Use fininstrument to create a FixedBond instrument object.
MaturityDate = datetime(2027,12,16); CouponRate = 0.01; FixedBondObj = fininstrument('FixedBond','CouponRate',CouponRate,'Maturity',MaturityDate);
Create ratecurve Object
Create a ratecurve object using ratecurve.
Settle = datetime(2022,10,10);
MarketDates = datetime([2023,9,15 ; 2024,9,15 ; 2025,9,15 ; 2026,9,15 ; 2027,9,15 ; 2028,9,15]);
ZeroDates = datetime([2023,10,15 ; 2024,10,15 ; 2025,10,15 ; 2026,10,15 ; 2027,10,15 ; 2028,10,15]);
ZeroRates = [4.2520 4.1081 3.8801 3.7170 3.6060 3.5250]'/100;
MarketSpreads = [97.9825 97.9825 97.9825 97.9825 97.9825 97.9825]';
RateObjB = ratecurve('zero',Settle,ZeroDates,ZeroRates+MarketSpreads(1)/10000); Create Discount Pricer Object
Use finpricer to create a Discount pricer object and use the ratecurve object with the 'DiscountCurve' name-value argument.
Pricer1 = finpricer("Discount",'DiscountCurve',RateObjB);
Price FixedBond Instrument
Use price to compute the price and sensitivities for the FixedBond instrument.
[Price1, outPR] = price(Pricer1, FixedBondObj,["all"])Price1 = 83.4210
outPR =
priceresult with properties:
Results: [1×2 table]
PricerData: []
Compute Bond Durations for FixedBond Instrument
Use bnddurp to compute the bond durations given the bond price.
[ModDuration, YearDuration, PerDuration] = bnddurp(Price1,FixedBondObj.CouponRate, Settle, FixedBondObj.Maturity,Period=FixedBondObj.Period)
ModDuration = 4.9169
YearDuration = 5.0308
PerDuration = 10.0616
Compute Key Rate Durations for FixedBond Instrument
Use bndkrdur to compute the FixedBond instrument key rate duration given a zero curve.
ZeroData1 = [datenum(RateObjB.Dates) RateObjB.Rates]; KeyRateDuration = bndkrdur(ZeroData1,FixedBondObj.CouponRate,Settle,FixedBondObj.Maturity)
KeyRateDuration = 1×6
0.0133 0.0212 0.0304 0.0389 4.0226 0.8164
This example shows the workflow to price multiple vanilla FixedBond instruments when you use a ratecurve and a Discount pricing method.
Create FixedBond Instrument Object
Use fininstrument to create a FixedBond instrument object for three Fixed Bond instruments.
FixB = fininstrument("FixedBond",'Maturity',datetime([2022,9,15 ; 2022,10,15 ; 2022,11,15]),'CouponRate',0.021,'Period',2,'Basis',1,'Principal',[100 ; 250 ; 500],'Name',"fixed_bond_instrument")
FixB=3×1 FixedBond array with properties:
CouponRate
Period
Basis
EndMonthRule
Principal
DaycountAdjustedCashFlow
BusinessDayConvention
Holidays
IssueDate
FirstCouponDate
LastCouponDate
StartDate
Maturity
Name
Create ratecurve Object
Create a ratecurve object using ratecurve.
Settle = datetime(2018,9,15); Type = 'zero'; ZeroTimes = [calmonths(6) calyears([1 2 3 4 5 7 10 20 30])]'; ZeroRates = [0.0052 0.0055 0.0061 0.0073 0.0094 0.0119 0.0168 0.0222 0.0293 0.0307]'; ZeroDates = Settle + ZeroTimes; myRC = ratecurve('zero',Settle,ZeroDates,ZeroRates)
myRC =
ratecurve with properties:
Type: "zero"
Compounding: -1
Basis: 0
Dates: [10×1 datetime]
Rates: [10×1 double]
Settle: 15-Sep-2018
InterpMethod: "linear"
ShortExtrapMethod: "next"
LongExtrapMethod: "previous"
Create Discount Pricer Object
Use finpricer to create a Discount pricer object and use the ratecurve object with the 'DiscountCurve' name-value pair argument.
outPricer = finpricer("Discount",'DiscountCurve',myRC)
outPricer =
Discount with properties:
DiscountCurve: [1×1 ratecurve]
Price FixedBond Instruments
Use price to compute the prices and sensitivities for the FixedBond instruments.
[Price, outPR] = price(outPricer, FixB,["all"])Price = 3×1
104.5679
261.4498
522.9174
outPR=1×3 priceresult array with properties:
Results
PricerData
outPR.Results
ans=1×2 table
Price DV01
______ ________
104.57 0.040397
ans=1×2 table
Price DV01
______ _____
261.45 0.103
ans=1×2 table
Price DV01
______ _______
522.92 0.21013
This example shows the workflow to price a stepped FixedBond instrument when you use a ratecurve and a Discount pricing method.
Create FixedBond Instrument Object
Use fininstrument to create a stepped FixedBond instrument object.
Maturity = datetime(2024,1,1); Period = 1; CDates = datetime([2020,1,1 ; 2024,1,1]); CRates = [.025; .03]; CouponRate = timetable(CDates,CRates); SBond = fininstrument("FixedBond",'Maturity',Maturity,'CouponRate',CouponRate,'Period',Period)
SBond =
FixedBond with properties:
CouponRate: [2×1 timetable]
Period: 1
Basis: 0
EndMonthRule: 1
Principal: 100
DaycountAdjustedCashFlow: 0
BusinessDayConvention: "actual"
Holidays: NaT
IssueDate: NaT
FirstCouponDate: NaT
LastCouponDate: NaT
StartDate: NaT
Maturity: 01-Jan-2024
Name: ""
Create ratecurve Object
Create a ratecurve object using ratecurve.
Settle = datetime(2018,1,1); ZeroTimes = calyears(1:10)'; ZeroRates = [0.0052 0.0055 0.0061 0.0073 0.0094 0.0119 0.0168 0.0222 0.0293 0.0307]'; ZeroDates = Settle + ZeroTimes; Compounding = 1; ZeroCurve = ratecurve("zero",Settle,ZeroDates,ZeroRates, "Compounding",Compounding)
ZeroCurve =
ratecurve with properties:
Type: "zero"
Compounding: 1
Basis: 0
Dates: [10×1 datetime]
Rates: [10×1 double]
Settle: 01-Jan-2018
InterpMethod: "linear"
ShortExtrapMethod: "next"
LongExtrapMethod: "previous"
Create Discount Pricer Object
Use finpricer to create a Discount pricer object and use the ratecurve object with the 'DiscountCurve' name-value pair argument.
outPricer = finpricer("Discount",'DiscountCurve',ZeroCurve)
outPricer =
Discount with properties:
DiscountCurve: [1×1 ratecurve]
Price FixedBond Instrument
Use price to compute the price and sensitivities for the vanilla FixedBond instrument.
[Price, outPR] = price(outPricer, SBond,["all"])Price = 109.6218
outPR =
priceresult with properties:
Results: [1×2 table]
PricerData: []
outPR.Results
ans=1×2 table
Price DV01
______ ________
109.62 0.061108
This example shows the workflow to price an amortizing FixedBond instrument when you use a ratecurve and a Discount pricing method.
Create FixedBond Instrument Object
Use fininstrument to create an amortizing FixedBond instrument object.
Maturity = datetime(2024,1,1); Period = 1; ADates = datetime([2020,1,1 ; 2024,1,1]); APrincipal = [100; 85]; Principal = timetable(ADates,APrincipal); Bondamort = fininstrument("FixedBond",'Maturity',Maturity,'CouponRate',0.025,'Period',Period,'Principal',Principal)
Bondamort =
FixedBond with properties:
CouponRate: 0.0250
Period: 1
Basis: 0
EndMonthRule: 1
Principal: [2×1 timetable]
DaycountAdjustedCashFlow: 0
BusinessDayConvention: "actual"
Holidays: NaT
IssueDate: NaT
FirstCouponDate: NaT
LastCouponDate: NaT
StartDate: NaT
Maturity: 01-Jan-2024
Name: ""
Create ratecurve Object
Create a ratecurve object using ratecurve.
Settle = datetime(2018,1,1); ZeroTimes = calyears(1:10)'; ZeroRates = [0.0052 0.0055 0.0061 0.0073 0.0094 0.0119 0.0168 0.0222 0.0293 0.0307]'; ZeroDates = Settle + ZeroTimes; Compounding = 1; ZeroCurve = ratecurve("zero",Settle,ZeroDates,ZeroRates, "Compounding",Compounding);
Create Discount Pricer Object
Use finpricer to create a Discount pricer object and use the ratecurve object for the 'DiscountCurve' name-value pair argument.
outPricer = finpricer("Discount",'DiscountCurve',ZeroCurve)
outPricer =
Discount with properties:
DiscountCurve: [1×1 ratecurve]
Price FixedBond Instrument
Use price to compute the price and sensitivities for the vanilla FixedBond instrument.
[Price, outPR] = price(outPricer,Bondamort,["all"])Price = 107.1273
outPR =
priceresult with properties:
Results: [1×2 table]
PricerData: []
outPR.Results
ans=1×2 table
Price DV01
______ ________
107.13 0.054279
This example shows the workflow to price a FixedBond instrument when using a HullWhite model and an IRMonteCarlo pricing method.
Create FixedBond Instrument Object
Use fininstrument to create a FixedBond instrument object.
FixB = fininstrument("FixedBond","Maturity",datetime(2022,9,15),"CouponRate",0.05,'Name',"fixed_bond")
FixB =
FixedBond with properties:
CouponRate: 0.0500
Period: 2
Basis: 0
EndMonthRule: 1
Principal: 100
DaycountAdjustedCashFlow: 0
BusinessDayConvention: "actual"
Holidays: NaT
IssueDate: NaT
FirstCouponDate: NaT
LastCouponDate: NaT
StartDate: NaT
Maturity: 15-Sep-2022
Name: "fixed_bond"
Create HullWhite Model Object
Use finmodel to create a HullWhite model object.
HullWhiteModel = finmodel("HullWhite",'Alpha',0.32,'Sigma',0.49)
HullWhiteModel =
HullWhite with properties:
Alpha: 0.3200
Sigma: 0.4900
Create ratecurve Object
Create a ratecurve object using ratecurve.
Settle = datetime(2019,1,1); Type = 'zero'; ZeroTimes = [calmonths(6) calyears([1 2 3 4 5 7 10 20 30])]'; ZeroRates = [0.0052 0.0055 0.0061 0.0073 0.0094 0.0119 0.0168 0.0222 0.0293 0.0307]'; ZeroDates = Settle + ZeroTimes; myRC = ratecurve('zero',Settle,ZeroDates,ZeroRates)
myRC =
ratecurve with properties:
Type: "zero"
Compounding: -1
Basis: 0
Dates: [10×1 datetime]
Rates: [10×1 double]
Settle: 01-Jan-2019
InterpMethod: "linear"
ShortExtrapMethod: "next"
LongExtrapMethod: "previous"
Create IRMonteCarlo Pricer Object
Use finpricer to create an IRMonteCarlo pricer object and use the ratecurve object for the 'DiscountCurve' name-value pair argument.
outPricer = finpricer("IRMonteCarlo",'Model',HullWhiteModel,'DiscountCurve',myRC,'SimulationDates',ZeroDates)
outPricer =
HWMonteCarlo with properties:
NumTrials: 1000
RandomNumbers: []
DiscountCurve: [1×1 ratecurve]
SimulationDates: [01-Jul-2019 01-Jan-2020 01-Jan-2021 01-Jan-2022 01-Jan-2023 01-Jan-2024 01-Jan-2026 01-Jan-2029 01-Jan-2039 01-Jan-2049]
Model: [1×1 finmodel.HullWhite]
Price FixedBond Instrument
Use price to compute the price and sensitivities for the FixedBond instrument.
[Price,outPR] = price(outPricer,FixB,["all"])Price = 115.0303
outPR =
priceresult with properties:
Results: [1×4 table]
PricerData: [1×1 struct]
outPR.Results
ans=1×4 table
Price Delta Gamma Vega
______ _______ ______ ____
115.03 -397.13 1430.4 0
This example shows the workflow to price a FixedBond instrument when using a HullWhite model and a IRTree pricing method.
Create FixedBond Instrument Object
Use fininstrument to create a FixedBond instrument object.
FixB = fininstrument("FixedBond","Maturity",datetime(2029,9,15),"CouponRate",.05,"Period",1,"Name","fixed_bond_instrument")
FixB =
FixedBond with properties:
CouponRate: 0.0500
Period: 1
Basis: 0
EndMonthRule: 1
Principal: 100
DaycountAdjustedCashFlow: 0
BusinessDayConvention: "actual"
Holidays: NaT
IssueDate: NaT
FirstCouponDate: NaT
LastCouponDate: NaT
StartDate: NaT
Maturity: 15-Sep-2029
Name: "fixed_bond_instrument"
Create ratecurve Object
Create a ratecurve object using ratecurve.
Settle = datetime(2019,9,15); Type = "zero"; ZeroTimes = [calyears([1:10])]'; ZeroRates = [0.0055 0.0061 0.0073 0.0094 0.0119 0.0168 0.0222 0.0293 0.0307 0.0310]'; ZeroDates = Settle + ZeroTimes; myRC = ratecurve('zero',Settle,ZeroDates,ZeroRates)
myRC =
ratecurve with properties:
Type: "zero"
Compounding: -1
Basis: 0
Dates: [10×1 datetime]
Rates: [10×1 double]
Settle: 15-Sep-2019
InterpMethod: "linear"
ShortExtrapMethod: "next"
LongExtrapMethod: "previous"
Create HullWhite Model Object
Use finmodel to create a HullWhite model object.
HullWhiteModel = finmodel("hullwhite",'Alpha',0.052,'Sigma',0.34)
HullWhiteModel =
HullWhite with properties:
Alpha: 0.0520
Sigma: 0.3400
Create IRTree Pricer Object
Use finpricer to create an IRTree pricer object and use the ratecurve object with the 'DiscountCurve' name-value pair argument.
HWTreePricer = finpricer("irtree","model",HullWhiteModel,"DiscountCurve",myRC,"TreeDates",ZeroDates)
HWTreePricer =
HWBKTree with properties:
Tree: [1×1 struct]
TreeDates: [10×1 datetime]
Model: [1×1 finmodel.HullWhite]
DiscountCurve: [1×1 ratecurve]
HWTreePricer.Tree
ans = struct with fields:
tObs: [0 1 1.9973 2.9945 3.9918 4.9918 5.9891 6.9863 7.9836 8.9836]
dObs: [15-Sep-2019 15-Sep-2020 15-Sep-2021 15-Sep-2022 15-Sep-2023 15-Sep-2024 15-Sep-2025 15-Sep-2026 15-Sep-2027 15-Sep-2028]
CFlowT: {[10×1 double] [9×1 double] [8×1 double] [7×1 double] [6×1 double] [5×1 double] [4×1 double] [3×1 double] [2×1 double] [9.9809]}
Probs: {[3×1 double] [3×3 double] [3×5 double] [3×7 double] [3×9 double] [3×11 double] [3×13 double] [3×15 double] [3×17 double]}
Connect: {[2] [2 3 4] [2 3 4 5 6] [2 3 4 5 6 7 8] [2 3 4 5 6 7 8 9 10] [2 3 4 5 6 7 8 9 10 11 12] [2 3 4 5 6 7 8 9 10 11 12 13 14] [2 3 4 5 6 7 8 9 10 11 12 13 14 15 16] [2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18]}
FwdTree: {1×10 cell}
RateTree: {1×10 cell}
Price FixedBond Instrument
Use price to compute the price and sensitivities for the FixedBond instrument.
[Price, outPR] = price(HWTreePricer, FixB,["all"])Price = 117.9440
outPR =
priceresult with properties:
Results: [1×4 table]
PricerData: [1×1 struct]
outPR.Results
ans=1×4 table
Price Delta Gamma Vega
______ _______ ______ ___________
117.94 -964.01 8868.6 -4.2633e-10
This example shows the workflow to price a FixedBond instrument when you use a CoxIngersollRoss model and an IRTree pricing method.
Create FixedBond Instrument Object
Use fininstrument to create a FixedBond instrument object.
Period = 1; Maturity = datetime(2027,1,1); CouponRate = 0.035; FixedBond = fininstrument("FixedBond",'Maturity',Maturity,'CouponRate',CouponRate,'Period',Period,Name="fixed_bond")
FixedBond =
FixedBond with properties:
CouponRate: 0.0350
Period: 1
Basis: 0
EndMonthRule: 1
Principal: 100
DaycountAdjustedCashFlow: 0
BusinessDayConvention: "actual"
Holidays: NaT
IssueDate: NaT
FirstCouponDate: NaT
LastCouponDate: NaT
StartDate: NaT
Maturity: 01-Jan-2027
Name: "fixed_bond"
Create CoxIngersollRoss Model Object
Use finmodel to create a CoxIngersollRoss model object.
alpha = 0.03;
theta = 0.02;
sigma = 0.1;
CIRModel = finmodel("CoxIngersollRoss",Sigma=sigma,Alpha=alpha,Theta=theta)CIRModel =
CoxIngersollRoss with properties:
Sigma: 0.1000
Alpha: 0.0300
Theta: 0.0200
Create ratecurve Object
Create a ratecurve object using ratecurve.
Times= [calyears([1 2 3 4 ])]';
Settle = datetime(2023,1,1);
ZRates = [0.035; 0.042147; 0.047345; 0.052707]';
ZDates = Settle + Times;
Compounding = -1;
Basis = 1;
ZeroCurve = ratecurve("zero",Settle,ZDates,ZRates,Compounding = Compounding, Basis = Basis);Create IRTree Pricer Object
Use finpricer to create an IRTree pricer object for the CoxIngersollRoss model and use the ratecurve object for the 'DiscountCurve' name-value argument.
CIRPricer = finpricer("irtree",Model=CIRModel,DiscountCurve=ZeroCurve,Maturity=ZDates(end),NumPeriods=length(ZDates))CIRPricer =
CIRTree with properties:
Tree: [1×1 struct]
TreeDates: [4×1 datetime]
Model: [1×1 finmodel.CoxIngersollRoss]
DiscountCurve: [1×1 ratecurve]
Price FixedBond Instrument
Use price to compute the price for the FixedBond instrument.
[Price,outPR] = price(CIRPricer,FixedBond,"all")Price = 93.4593
outPR =
priceresult with properties:
Results: [1×4 table]
PricerData: [1×1 struct]
outPR.Results
ans=1×4 table
Price Delta Gamma Vega
______ _______ ______ ___________
93.459 -354.23 1384.8 -1.4211e-10
This example shows the workflow for using FixedBond instruments that are fit to a Svensson model using fitSvensson.
Define the bond data and use fininstrument to create FixedBond instrument objects.
settle = datetime(2009,11,24)
settle = datetime
24-Nov-2009
maturity = settle + calyears([1;2;3;5;7;10;20;30])
maturity = 8×1 datetime
24-Nov-2010
24-Nov-2011
24-Nov-2012
24-Nov-2014
24-Nov-2016
24-Nov-2019
24-Nov-2029
24-Nov-2039
price = [100.1; 100.1; 100.2; 99.0; ... 100.8; 99.2; 101.7; 100.2]; coupon = [0.020; 0.0275; 0.035; 0.042; ... 0.0475; 0.0525; 0.055; 0.052]; Bonds = fininstrument("FixedBond",'Maturity',maturity,'CouponRate',coupon)
Bonds=8×1 FixedBond array with properties:
CouponRate
Period
Basis
EndMonthRule
Principal
DaycountAdjustedCashFlow
BusinessDayConvention
Holidays
IssueDate
FirstCouponDate
LastCouponDate
StartDate
Maturity
Name
Use fitSvensson to create a parameter curve object.
lb = [-Inf -Inf -Inf -Inf 0 0]; ub = [Inf Inf Inf Inf 5 20]; x0 = [.5 .5 .5 .5 2 5]; SvenModel = fitSvensson(settle,Bonds,price,'x0',x0,'lb',lb,'ub',ub)
Local minimum possible. lsqnonlin stopped because the final change in the sum of squares relative to its initial value is less than the value of the function tolerance. <stopping criteria details>
SvenModel =
parametercurve with properties:
Type: "zero"
Settle: 24-Nov-2009
Compounding: -1
Basis: 0
FunctionHandle: @(t)fitF(Params,t)
Parameters: [0.0290 -0.0217 0.0025 0.0973 1.7800 7.5294]
p = SvenModel.Parameters
p = 1×6
0.0290 -0.0217 0.0025 0.0973 1.7800 7.5294
maturities = settle(1) + calmonths(1:360)
maturities = 1×360 datetime
24-Dec-2009 24-Jan-2010 24-Feb-2010 24-Mar-2010 24-Apr-2010 24-May-2010 24-Jun-2010 24-Jul-2010 24-Aug-2010 24-Sep-2010 24-Oct-2010 24-Nov-2010 24-Dec-2010 24-Jan-2011 24-Feb-2011 24-Mar-2011 24-Apr-2011 24-May-2011 24-Jun-2011 24-Jul-2011 24-Aug-2011 24-Sep-2011 24-Oct-2011 24-Nov-2011 24-Dec-2011 24-Jan-2012 24-Feb-2012 24-Mar-2012 24-Apr-2012 24-May-2012 24-Jun-2012 24-Jul-2012 24-Aug-2012 24-Sep-2012 24-Oct-2012 24-Nov-2012 24-Dec-2012 24-Jan-2013 24-Feb-2013 24-Mar-2013 24-Apr-2013 24-May-2013 24-Jun-2013 24-Jul-2013 24-Aug-2013 24-Sep-2013 24-Oct-2013 24-Nov-2013 24-Dec-2013 24-Jan-2014 24-Feb-2014 24-Mar-2014 24-Apr-2014 24-May-2014 24-Jun-2014 24-Jul-2014 24-Aug-2014 24-Sep-2014 24-Oct-2014 24-Nov-2014 24-Dec-2014 24-Jan-2015 24-Feb-2015 24-Mar-2015 24-Apr-2015 24-May-2015 24-Jun-2015 24-Jul-2015 24-Aug-2015 24-Sep-2015 24-Oct-2015 24-Nov-2015 24-Dec-2015 24-Jan-2016 24-Feb-2016 24-Mar-2016 24-Apr-2016 24-May-2016 24-Jun-2016 24-Jul-2016 24-Aug-2016 24-Sep-2016 24-Oct-2016 24-Nov-2016 24-Dec-2016 24-Jan-2017 24-Feb-2017 24-Mar-2017 24-Apr-2017 24-May-2017 24-Jun-2017 24-Jul-2017 24-Aug-2017 24-Sep-2017 24-Oct-2017 24-Nov-2017 24-Dec-2017 24-Jan-2018 24-Feb-2018 24-Mar-2018 24-Apr-2018 24-May-2018 24-Jun-2018 24-Jul-2018 24-Aug-2018 24-Sep-2018 24-Oct-2018 24-Nov-2018 24-Dec-2018 24-Jan-2019 24-Feb-2019 24-Mar-2019 24-Apr-2019 24-May-2019 24-Jun-2019 24-Jul-2019 24-Aug-2019 24-Sep-2019 24-Oct-2019 24-Nov-2019 24-Dec-2019 24-Jan-2020 24-Feb-2020 24-Mar-2020 24-Apr-2020 24-May-2020 24-Jun-2020 24-Jul-2020 24-Aug-2020 24-Sep-2020 24-Oct-2020 24-Nov-2020 24-Dec-2020 24-Jan-2021 24-Feb-2021 24-Mar-2021 24-Apr-2021 24-May-2021 24-Jun-2021 24-Jul-2021 24-Aug-2021 24-Sep-2021 24-Oct-2021 24-Nov-2021 24-Dec-2021 24-Jan-2022 24-Feb-2022 24-Mar-2022 24-Apr-2022 24-May-2022 24-Jun-2022 24-Jul-2022 24-Aug-2022 24-Sep-2022 24-Oct-2022 24-Nov-2022 24-Dec-2022 24-Jan-2023 24-Feb-2023 24-Mar-2023 24-Apr-2023 24-May-2023 24-Jun-2023 24-Jul-2023 24-Aug-2023 24-Sep-2023 24-Oct-2023 24-Nov-2023 24-Dec-2023 24-Jan-2024 24-Feb-2024 24-Mar-2024 24-Apr-2024 24-May-2024 24-Jun-2024 24-Jul-2024 24-Aug-2024 24-Sep-2024 24-Oct-2024 24-Nov-2024 24-Dec-2024 24-Jan-2025 24-Feb-2025 24-Mar-2025 24-Apr-2025 24-May-2025 24-Jun-2025 24-Jul-2025 24-Aug-2025 24-Sep-2025 24-Oct-2025 24-Nov-2025 24-Dec-2025 24-Jan-2026 24-Feb-2026 24-Mar-2026 24-Apr-2026 24-May-2026 24-Jun-2026 24-Jul-2026 24-Aug-2026 24-Sep-2026 24-Oct-2026 24-Nov-2026 24-Dec-2026 24-Jan-2027 24-Feb-2027 24-Mar-2027 24-Apr-2027 24-May-2027 24-Jun-2027 24-Jul-2027 24-Aug-2027 24-Sep-2027 24-Oct-2027 24-Nov-2027 24-Dec-2027 24-Jan-2028 24-Feb-2028 24-Mar-2028 24-Apr-2028 24-May-2028 24-Jun-2028 24-Jul-2028 24-Aug-2028 24-Sep-2028 24-Oct-2028 24-Nov-2028 24-Dec-2028 24-Jan-2029 24-Feb-2029 24-Mar-2029 24-Apr-2029 24-May-2029 24-Jun-2029 24-Jul-2029 24-Aug-2029 24-Sep-2029 24-Oct-2029 24-Nov-2029 24-Dec-2029 24-Jan-2030 24-Feb-2030 24-Mar-2030 24-Apr-2030 24-May-2030 24-Jun-2030 24-Jul-2030 24-Aug-2030 24-Sep-2030 24-Oct-2030 24-Nov-2030 24-Dec-2030 24-Jan-2031 24-Feb-2031 24-Mar-2031 24-Apr-2031 24-May-2031 24-Jun-2031 24-Jul-2031 24-Aug-2031 24-Sep-2031 24-Oct-2031 24-Nov-2031 24-Dec-2031 24-Jan-2032 24-Feb-2032 24-Mar-2032 24-Apr-2032 24-May-2032 24-Jun-2032 24-Jul-2032 24-Aug-2032 24-Sep-2032 24-Oct-2032 24-Nov-2032 24-Dec-2032 24-Jan-2033 24-Feb-2033 24-Mar-2033 24-Apr-2033 24-May-2033 24-Jun-2033 24-Jul-2033 24-Aug-2033 24-Sep-2033 24-Oct-2033 24-Nov-2033 24-Dec-2033 24-Jan-2034 24-Feb-2034 24-Mar-2034 24-Apr-2034 24-May-2034 24-Jun-2034 24-Jul-2034 24-Aug-2034 24-Sep-2034 24-Oct-2034 24-Nov-2034 24-Dec-2034 24-Jan-2035 24-Feb-2035 24-Mar-2035 24-Apr-2035 24-May-2035 24-Jun-2035 24-Jul-2035 24-Aug-2035 24-Sep-2035 24-Oct-2035 24-Nov-2035 24-Dec-2035 24-Jan-2036 24-Feb-2036 24-Mar-2036 24-Apr-2036 24-May-2036 24-Jun-2036 24-Jul-2036 24-Aug-2036 24-Sep-2036 24-Oct-2036 24-Nov-2036 24-Dec-2036 24-Jan-2037 24-Feb-2037 24-Mar-2037 24-Apr-2037 24-May-2037 24-Jun-2037 24-Jul-2037 24-Aug-2037 24-Sep-2037 24-Oct-2037 24-Nov-2037 24-Dec-2037 24-Jan-2038 24-Feb-2038 24-Mar-2038 24-Apr-2038 24-May-2038 24-Jun-2038 24-Jul-2038 24-Aug-2038 24-Sep-2038 24-Oct-2038 24-Nov-2038 24-Dec-2038 24-Jan-2039 24-Feb-2039 24-Mar-2039 24-Apr-2039 24-May-2039 24-Jun-2039 24-Jul-2039 24-Aug-2039 24-Sep-2039 24-Oct-2039 24-Nov-2039
rates = zerorates(SvenModel,maturities)
rates = 1×360
0.0083 0.0094 0.0105 0.0114 0.0124 0.0134 0.0143 0.0153 0.0162 0.0171 0.0179 0.0188 0.0196 0.0204 0.0212 0.0219 0.0226 0.0234 0.0241 0.0248 0.0255 0.0262 0.0268 0.0275 0.0281 0.0287 0.0293 0.0299 0.0304 0.0310 0.0316 0.0321 0.0326 0.0332 0.0336 0.0342 0.0346 0.0351 0.0356 0.0360 0.0365 0.0369 0.0373 0.0377 0.0382 0.0386 0.0389 0.0393 0.0397 0.0401
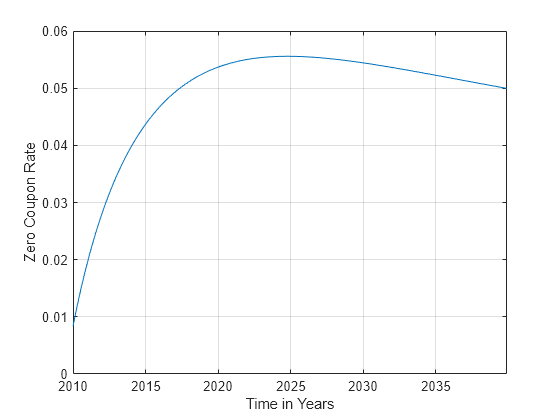
Plot the zero coupon rate.
plot(maturities,rates) xtickformat('yyyy') grid('on') xlabel('Time in Years') ylabel('Zero Coupon Rate')
More About
A fixed-rate note is a long-term debt security with a preset interest rate and maturity, by which the interest must be paid.
The principal might or might not be paid at maturity. In Financial Instruments Toolbox™, the principal is always paid at maturity. For more information, see Fixed-Rate Note.
A vanilla coupon bond is a security representing an obligation to repay a borrowed amount at a designated time and to make periodic interest payments until that time.
The issuer of a bond makes the periodic interest payments until the bond matures. At maturity, the issuer pays to the holder of the bond the principal amount owed (face value) and the last interest payment.
A step-up bond and a step-down bond are debt securities with a predetermined coupon structure over time.
With these instruments, coupons increase (step up) or decrease (step down) at specific times during the life of the bond.
An amortized bond is treated as an asset, with the discount amount being amortized to interest expense over the life of the bond.
Version History
Introduced in R2020aYou can price FixedBond instruments using a CoxIngersollRoss model object
and an IRTree pricing
method.
Although FixedBond supports serial date numbers,
datetime values are recommended instead. The
datetime data type provides flexible date and time
formats, storage out to nanosecond precision, and properties to account for time
zones and daylight saving time.
To convert serial date numbers or text to datetime values, use the datetime function. For example:
t = datetime(738427.656845093,"ConvertFrom","datenum"); y = year(t)
y =
2021
There are no plans to remove support for serial date number inputs.
See Also
Functions
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Website auswählen
Wählen Sie eine Website aus, um übersetzte Inhalte (sofern verfügbar) sowie lokale Veranstaltungen und Angebote anzuzeigen. Auf der Grundlage Ihres Standorts empfehlen wir Ihnen die folgende Auswahl: .
Sie können auch eine Website aus der folgenden Liste auswählen:
So erhalten Sie die bestmögliche Leistung auf der Website
Wählen Sie für die bestmögliche Website-Leistung die Website für China (auf Chinesisch oder Englisch). Andere landesspezifische Websites von MathWorks sind für Besuche von Ihrem Standort aus nicht optimiert.
Amerika
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)