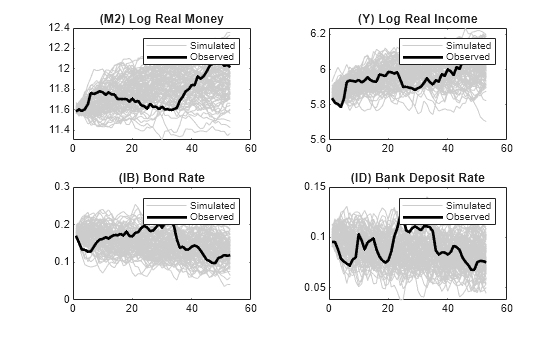
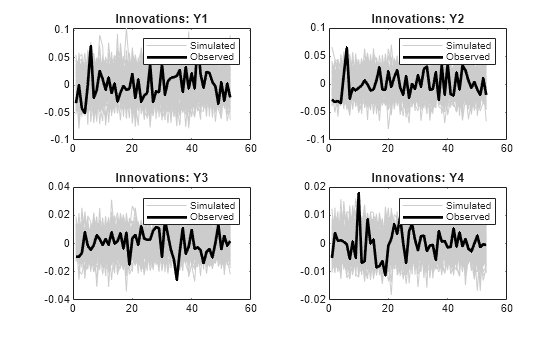
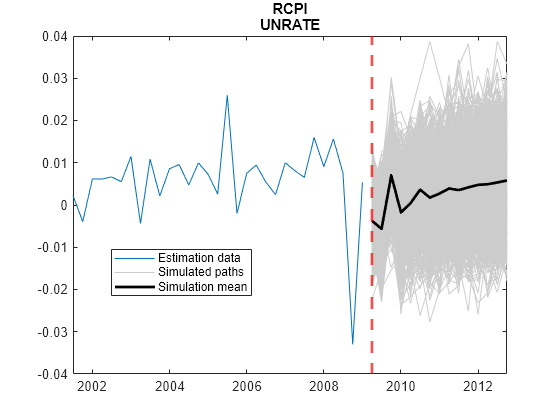
simulate
Monte Carlo simulation of vector autoregression (VAR) model
Syntax
Description
Conditional and Unconditional Simulation for Numeric Arrays
Y = simulate(Mdl,numobs,Name=Value)simulate returns numeric arrays when all optional
input data are numeric arrays. For example,
simulate(Mdl,100,NumPaths=1000,Y0=PS) returns a numeric
array of 1000, 100-period simulated response paths from
Mdl and specifies the numeric array of presample
response data PS.
To produce a conditional simulation, specify response data in the simulation
horizon by using the YF name-value argument.
Unconditional Simulation for Tables and Timetables
Tbl = simulate(Mdl,numobs,Presample=Presample)Tbl containing the random
multivariate response and innovations variables, which results from the
unconditional simulation of the response series in the model
Mdl. simulate uses the table or
timetable of presample data Presample to initialize the
response series. (since R2022b)
simulate selects the variables in
Mdl.SeriesNames to simulate, or it selects all variables
in Presample. To select different response variables in
Tbl to simulate, use the
PresampleResponseVariables name-value argument.
Tbl = simulate(Mdl,numobs,Presample=Presample,Name=Value)simulate(Mdl,100,Presample=PSTbl,PresampleResponseVariables=["GDP"
"CPI"]) returns a timetable of variables containing 100-period
simulated response and innovations series from Mdl,
initialized by the data in the GDP and CPI
variables of the timetable of presample data in PSTbl. (since R2022b)
Conditional Simulation for Tables and Timetables
Tbl = simulate(Mdl,numobs,InSample=InSample,ResponseVariables=ResponseVariables)Tbl containing the random
multivariate response and innovations variables, which results from the
conditional simulation of the response series in the model
Mdl. InSample is a table or
timetable of response or predictor data in the simulation horizon that
simulate uses to perform the conditional simulation
and ResponseVariables specifies the response variables in
InSample. (since R2022b)
Tbl = simulate(___,Name=Value)
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
Suppose Y0 and YF are the presample and future
response data specified by the numeric data inputs in Y0 and
YF or the selected variables from the input tables or
timetables Presample and InSample. Similarly,
suppose E contains the simulated model innovations as returned in the
numeric array E or the table or timetable
Tbl.
simulateperforms conditional simulation using this process for all pagesk= 1,...,numpathsand for each timet= 1,...,numobs.simulateinfers (or inverse filters) the model innovations for all response variables (E(from the known future responses (t,:,k)YF(). Int,:,k)E,simulatemimics the pattern ofNaNvalues that appears inYF.For the missing elements of
Eat timet,simulateperforms these steps.Draw
Z1, the random, standard Gaussian distribution disturbances conditional on the known elements ofE.Scale
Z1by the lower triangular Cholesky factor of the conditional covariance matrix. That is,Z2=L*Z1, whereL=chol(C,"lower")andCis the covariance of the conditional Gaussian distribution.Impute
Z2in place of the corresponding missing values inE.
For the missing values in
YF,simulatefilters the corresponding random innovations through the modelMdl.
simulateuses this process to determine the time origin t0 of models that include linear time trends.If you do not specify
Y0, then t0 = 0.Otherwise,
simulatesets t0 tosize(Y0,1)–Mdl.P. Therefore, the times in the trend component are t = t0 + 1, t0 + 2,..., t0 +numobs. This convention is consistent with the default behavior of model estimation in whichestimateremoves the firstMdl.Presponses, reducing the effective sample size. Althoughsimulateexplicitly uses the firstMdl.Ppresample responses inY0to initialize the model, the total number of observations inY0(excluding any missing values) determines t0.
References
[1] Hamilton, James D. Time Series Analysis. Princeton, NJ: Princeton University Press, 1994.
[2] Johansen, S. Likelihood-Based Inference in Cointegrated Vector Autoregressive Models. Oxford: Oxford University Press, 1995.
[3] Juselius, K. The Cointegrated VAR Model. Oxford: Oxford University Press, 2006.
[4] Lütkepohl, H. New Introduction to Multiple Time Series Analysis. Berlin: Springer, 2005.