fdesign.arbgrpdelay
Arbitrary group delay filter specification object
Syntax
Description
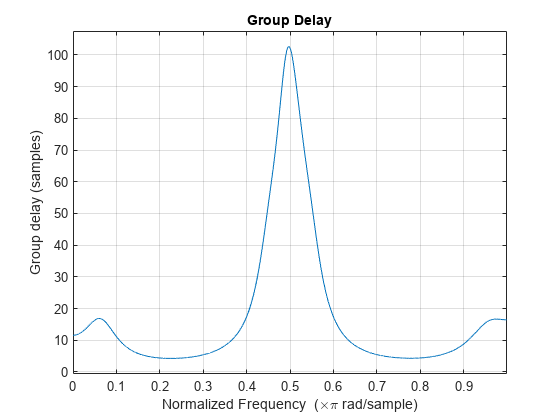
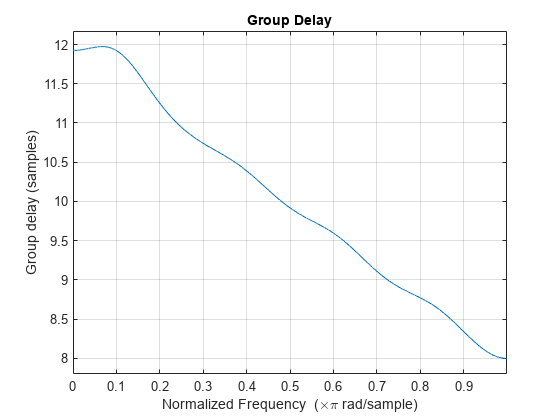
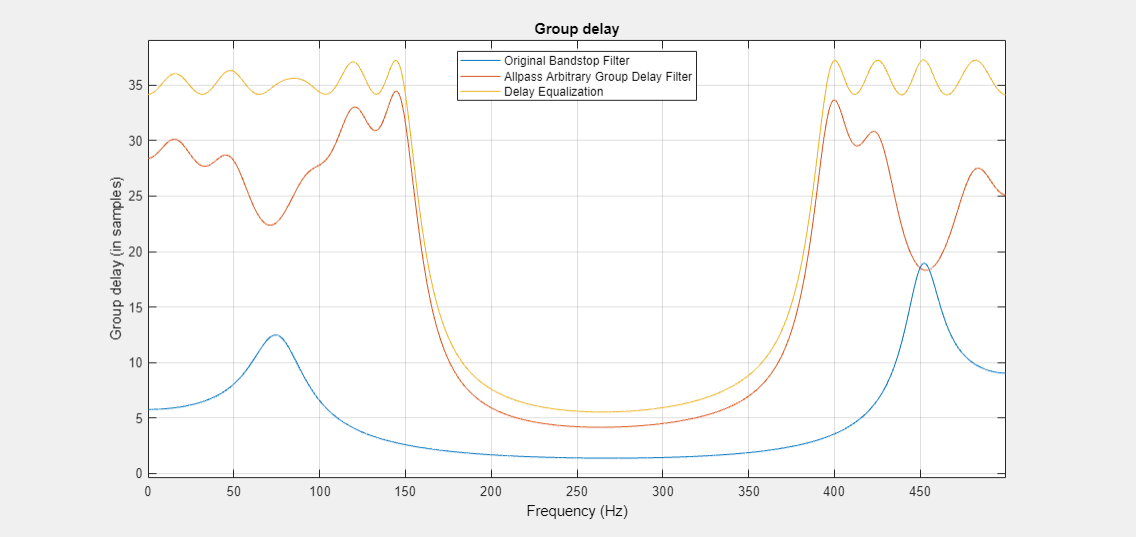
Arbitrary group delay filters are allpass filters that you can use to correct
the phase distortion introduced by other filters. The
fdesign.arbgrpdelay function uses an iterative least
p-th norm optimization procedure to minimize the phase response
error [1].
The fdesign.arbgrpdelay function returns a filter design
specification object containing filter specifications, such as filter order, number of
bands, frequency vector, and group delay response. You then use the design function to design the filter from the filter design
specifications object.
For more control options, see Filter Design Procedure. For a complete workflow, see Design a Filter in Fdesign — Process Overview.
specObj = fdesign.arbgrpdelay
specObj = fdesign.arbgrpdelay(spec,value1,...,valueN)value1,...,valueN. Set the specification options in the
expression spec. After the expression, specify a value for each
option.
specObj = fdesign.arbgrpdelay(___,Fs)
Examples
Input Arguments
Output Arguments
More About
Tips
If your arbitrary group delay design produces the Poorly conditioned Hessian
matrix error, perform one of the following or both.
Set the
MaxPoleRadiusIIR lp norm design option to a number less than 1 when youdesignyour filter.For more information on thedesign(d,'iirlpnorm','MaxPoleRadius',0.95)
MaxPoleRadiusdesign option, see the Design Arbitrary Group Delay and Multiband Delay Equalization examples.Reduce the order of your filter design.
Algorithms
The fdesign.arbgrpdelay function uses a least p-th
norm iterative optimization described in [1].
References
[1] Antoniou, A. Digital Signal Processing: Signals, Systems, and Filters., New York:McGraw-Hill, 2006, pp. 719–771.
Version History
Introduced in R2011b
See Also
fdesign | design | iirgrpdelay | designmethods | designoptions