logsig

Log-Sigmoid-Transferfunktion

Syntax

A = logsig(N)

dA_dN = logsig('dn',N,A,FP)

info = logsig(code)

Beschreibung

Tipp

Um eine Log-Sigmoid-Aktivierung für Deep Learning zu verwenden, benutzen Sie die Funktion sigmoidLayer oder die dlarray-Methode „Sigmoid“.

A = logsig(N) nimmt eine Matrix von Netzeingangsvektoren, N und gibt die S-mal-Q-Matrix A zurück, mit den Elementen von N in [0, 1] gepresst.

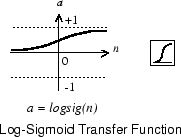
logsig ist eine Transferfunktion. Transferfunktionen berechnen den Ausgang einer Schicht aus ihrem Netzeingang.

dA_dN = logsig('dn',N,A,FP) gibt die S-mal-Q-Ableitung von A bezüglich N aus. Wenn A oder FP nicht angegeben wird oder auf [] gesetzt ist, wird FP auf die Standardparameter zurückgesetzt und A wird aus N berechnet.

info = logsig(code) gibt Informationen über diese Funktion aus. Weitere Informationen finden Sie in der Beschreibung des Arguments code.

Beispiele

Erstellen eines Diagramms der Transferfunktion logsig

Dieses Beispiel zeigt, wie man die Log-Sigmoid-Transferfunktion einer Eingangsmatrix berechnet und plottet.

Erstellen Sie die Eingangsmatrix n. Rufen Sie dann die Funktion logsig auf und stellen Sie die Ergebnisse dar.

n = -5:0.1:5;
a = logsig(n);
plot(n,a)

Ordnen Sie diese Übertragungsfunktion der Schicht i eines Netzes zu.

net.layers{i}.transferFcn = 'logsig';

Eingabeargumente

N — Eingangsmatrix

Matrix

Netto-Eingangsspaltenvektoren, angegeben als S-mal-Q-Matrix.

code — Informationsoption

'name' | 'output' | 'active' | 'fullderiv' | 'fpnames' | 'fpdefaults'

Informationen, die Sie aus der Funktion abrufen möchten, angegeben als eines der folgenden Argumente:

• 'name' gibt den Namen dieser Funktion aus.

• 'output' gibt den Ausgabebereich [min max] aus.

• 'active' gibt den aktiven Eingangsbereich [min max] aus.

• 'fullderiv' gibt 1 oder 0 aus, je nachdem, ob dA_dN S-malS-malQ oder S-mal-Q ist.

• 'fpnames' gibt die Namen der Funktionsparameter aus.

• 'fpdefaults' gibt die Standard-Funktionsparameter aus.

Ausgangsargumente

A — Ausgangsmatrix

Matrix

Ausgangsvektoren, zurückgegeben als S-mal-Q-Matrix, wobei jedes Element von N mit einer „S-förmigen“ Funktion aus dem Intervall [-inf inf] auf das Intervall [0 1] gepresst wird.

Algorithmen

logsig(n) = 1 / (1 + exp(-n))

Versionsverlauf

Eingeführt vor R2006a

Siehe auch

sim | tansig