M-FSK Modulator Baseband

Modulate using M-ary frequency shift keying method

• 

Libraries:
Communications Toolbox / Modulation / Digital Baseband Modulation / FM

Description

The M-FSK Modulator Baseband block modulates a signal using the M-ary frequency shift keying (M-FSK) method.

To prevent aliasing in the output signal, set the sampling frequency to a value greater than the product of the M-ary number and the Frequency separation (Hz) parameter values. The sampling frequency is the Samples per symbol parameter value divided by the input symbol period (in seconds) defined for the model.

Examples

FSK Modulation in AWGN

Pass a 2-FSK-modulated signal through an additive white Gaussian noise (AWGN) channel. Demodulate the received signal and calculate the symbol error rate (SER).

The cm_2fsk_mod_demod model 2-FSK-modulates a random binary signal, applies AWGN, and then 2-FSK-demodulates the signal. An Error Rate Calculation block computes the SER. In the Error Rate Calculation block, a setting of 1 for the Receive delay parameter accounts for a 1 sample delay.

model = 'cm_2fsk_mod_demod';
open_system(model);
chan = [model,'/AWGN Channel'];

Display the computed SER with Es/N0 set to 10. A Scope (Simulink) block plots the time domain input and demodulated signals, and a signal that indicates when the two signals are not equal.

set_param(chan,'esno','10');
sim(model);
fprintf('With EsN0 set to 10, SER = %7.6f\n',ErrorVec(1));

With EsN0 set to 10, SER = 0.004889

M-FSK-Modulate and -Demodulate Integer and Binary Values in Simulink

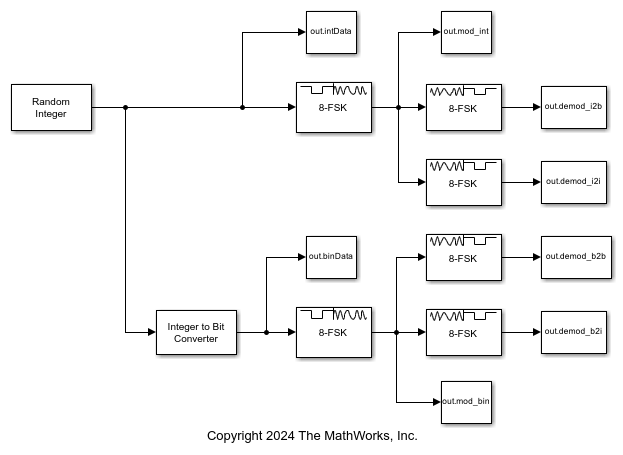
M-FSK-modulate and -demodulate input integer and binary data. Each integer or group of log2(M) bits corresponds to one symbol, where M represents the M-ary number parameter value. Compute the expected signal lengths for the input and output signals. Display the expected and resulting lengths for the input and output signals.

The cm_fsk_mod_demod_bin_int model has two parallel processing paths that modulate and demodulate the input data.

The modulator and demodulator pairs are configured for 8-ary modulation order, 100 Hz frequency separation, 21 samples per frame, and 10 samples per symbol. The model initializes the variables that configure the block parameters by using the PreLoadFcn callback function. For more information, see Model Callbacks (Simulink).

• The upper path modulates data by using an 8-FSK Modulator block configured to accept integer data, and then demodulates the data and outputs binary and integer data from separate 8-FSK Demodulator blocks.

• The lower path modulates data by using an 8-FSK Modulator block configured to accept binary data, and also demodulates the data and outputs binary and integer data from separate 8-FSK Demodulator blocks.

Run the model and compute the expected and resulting input and output signal lengths. Display the signal lengths to confirm that the results match the expected lengths.

Display the expected input and output lengths for a binary input signal.

Nbit  Nsym  Nbout  Niout 
 693   2310   693   231

Display the resulting input and output lengths for a binary input signal.

 bit   sym   bout   iout
 693   2310   693   231

Display the expected input and output lengths for an integer input signal.

Nint  Nsym  Nibout  Niiout 
 231   2310   693   231

Display the resulting input and output lengths for an integer input signal.

 bit   sym   bout   iout
 231   2310   693   231

Ports

Input

In — Input signal

scalar | row vector

Input signal, specified as a scalar or column vector. For more information, see Input type.

This port is unnamed on the block.

Data Types: double

Output

Out — M-FSK-modulated signal

scalar | column vector

M-FSK-modulated signal, returned as a scalar or column vector of complex symbols. For more information, see Single-Rate Processing and Multirate Processing.

The output is a baseband representation of the modulated signal. The Output data type parameter specifies the desired output data type.

This port is unnamed on the block.

Data Types: double

Parameters

To edit block parameters interactively, use the Property Inspector. From the Simulink^® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.

M-ary number — Number of frequencies in modulated signal

8 (default) | positive integer ≥ 2

Number of frequencies in the modulated signal, specified as a positive integer ≥ 2.

Input type — Integer or group of bits input indicator

Integer (default) | Bit

Indicates whether the input consists of integers or groups of bits, specified as Integer or Bit.

If you set this parameter to Bit, then the M-ary number parameter must be 2^K for some positive integer K.

Symbol set ordering — Symbol mapping

Binary (default) | Gray

Symbol mapping of input symbols, specified as Binary or Gray.

• Set this parameter to Binary to map symbols using binary-coded ordering.

• Set this parameter to Gray to map symbols using Gray-coded ordering. For Gray-coded ordering, the M-ary number value must be a power of two.

For more information, see Integer-Valued Signals and Binary-Valued Signals.

Frequency separation (Hz) — Frequency separation in Hz

6 (default) | positive scalar

Frequency separation in Hz, specified as a positive scalar representing the distance between successive frequencies in the modulated signal.

Phase continuity — Phase continuity

Continuous (default) | Discontinuous

Phase continuity, specified as Continuous or Discontinuous to determine whether the modulated signal changes phases in a continuous or discontinuous way.

• If you set this parameter to Continuous, then the modulated signal maintains its phase even when it changes its frequency.

• If you set this parameter to Discontinuous, then the modulated signal comprises portions of M sinusoids of different frequencies. A change in the input value sometimes causes a change in the phase of the modulated signal. M is the M-ary number parameter value.

Samples per symbol — Symbol sampling rate

17 (default) | positive integer

Symbol sampling rate, specified as a positive integer representing the number of output samples that the block produces for each integer or binary word in the input.

For more information, see Signal Upsampling and Rate Changes.

Rate options — Block processing rate

Enforce single-rate processing (default) | Allow multirate processing

Block processing rate, specified as one of these options:

• Enforce single-rate processing — The input and output signals have the same sample time. The block implements the rate change by making a size change at the output when compared to the input. The output width equals the product of the number of symbols and the Samples per symbol parameter value.

• Allow multirate processing — The input and output signals have different sample times. The output sample time equals the symbol period divided by the Samples per symbol parameter value.

Output data type — Output data type

double (default) | single

Output data type, specified as double or single.

Block Characteristics

Data Types	Boolean | double | integer | single
Multidimensional Signals	no
Variable-Size Signals	no

More About

Integer-Valued Signals and Binary-Valued Signals

The input and output signals for this block are discrete-time signals.

When you set the Input type parameter to Integer, the block accepts integer values in the range [0, (M–1)]. M is the modulation order as specified by the M-ary number block parameter.

When you set the Input type parameter to Bit, the block accepts binary-valued inputs that represent integers. The block collects binary-valued signals into groups of K = log₂(M) bits, where K represents the number of bits per symbol.

The input vector length must be an integer multiple of K. In this configuration, the block accepts a group of K bits and maps that group onto a symbol at the block output. The block outputs one modulated symbol, oversampled by the Samples per symbol parameter value, for each group of K bits.

The Symbol set ordering parameter indicates how the block maps a group of K input bits to a corresponding symbol.

• When you set the Symbol set ordering parameter to Binary, the block maps [u(1) u(2) … u(K)] to the integer

  $${\displaystyle \sum _{i=1}^{K}u(i)2^{K-i}}$$

  and assumes that this integer is the input value. u(1) is the most significant bit. With binary symbol set ordering and the M-ary number parameter value set to 8, the block produces the same output when the Input type parameter is

  • Integer and input is the integer 6.

  • Bit and the binary input word [1 1 0].

• When you set Symbol set ordering to Gray, the block uses a Gray-coded arrangement and assigns binary inputs to points of a predefined Gray-coded signal constellation. The predefined M-ary Gray-coded signal constellation assigns the bit representation in the Pth row of bit matrix b to the Pth integer, where the left-most bit is the most significant bit (MSB). This code sample defines a Gray-coded bit array for M = 8.

  M = 8;
  K = log2(M); % Number of bits per symbol
  P = [0:M-1];
  b = int2bit(bitxor(P,floor(P/2)),K)
  b = reshape(b,K,[])'
  

  As an example, this table shows how the block maps integers to binary- and Gray-coded bit symbols for M = 8.

Symbol Mapping for Binary and Gray Codes

Binary Code		Gray Code
Integer	Bit	Integer	Bit
0	000	0	000
1	001	1	001
2	010	3	011
3	011	2	010
4	100	6	110
5	101	7	111
6	110	5	101
7	111	4	100

Single-Rate Processing

In single-rate processing mode, the input and output signals have the same port sample time. The block implicitly implements the rate change by making a size change at the output when compared to the input. In this mode, the input to the block can be multiple symbols.

• When you set Input type to Integer, the input can be a column vector, the length of which is the number of input symbols.

• When you set Input type to Bit, the input width must be an integer multiple of K, the number of bits per symbol, and the M-ary number value must be a power of two.

The output width equals the product of the number of input symbols and the Samples per symbol parameter value.

Multirate Processing

In multirate processing mode, the input and output signals have different port sample times. In this mode, the input to the block must be one symbol.

• When you set Input type to Integer, the input must be a scalar.

• When you set Input type to Bit, the input width must equal the number of bits per symbol, K, and the M-ary number value must be a power of two.

The output sample time equals the symbol period divided by the M-ary number parameter value.

To run the M-FSK Modulator block in multirate mode, clear the Treat each discrete rate as a separate task check box (in Simulation > Configuration Parameters > Solver).

Algorithms

As described in Sklar [1], the general analytical expression for M-FSK modulation is

$$s_i(t)=\sqrt{\frac{2E}{T}\cos ({\omega }_{i}t+\varphi )}\begin{array}{cc}& \begin{array}{c}\text{0}\le t\le T\\ i\text{=1,}\mathrm{...}\text{,}M\end{array}\end{array}$$

• E is the symbol energy.

• T is the symbol time duration.

• ω_i is the frequency term that has M discrete values.

• M is the modulation order and specifies the number of waveforms.

• ϕ is the phase offset.

References

[1] Sklar, Bernard. Digital Communications: Fundamentals and Applications. 2nd ed. Upper Saddle River, NJ: Prentice-Hall PTR, 2001.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced before R2006a