comm.DecisionFeedbackEqualizer
Equalize modulated signals using decision feedback filtering
Description
The comm.DecisionFeedbackEqualizer
System object™ uses a decision feedback filter tap delay line with a weighted sum to equalize
modulated signals transmitted through a dispersive channel. The equalizer object adaptively
adjusts tap weights based on the selected algorithm. For more information, see Algorithms.
To equalize modulated signals using a decision feedback filter:
Create the
comm.DecisionFeedbackEqualizerobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Description
dfe = comm.DecisionFeedbackEqualizer
dfe = comm.DecisionFeedbackEqualizer(Name,Value)comm.DecisionFeedbackEqualizer('Algorithm','RLS') configures the
equalizer object to update tap weights using the recursive least squares (RLS) algorithm.
Enclose each property name in quotes.
Properties
Unless otherwise indicated, properties are nontunable, which means you cannot change their
values after calling the object. Objects lock when you call them, and the
release function unlocks them.
If a property is tunable, you can change its value at any time.
For more information on changing property values, see System Design in MATLAB Using System Objects.
Adaptive algorithm used for equalization, specified as one of these values:
'LMS'— Update the equalizer tap weights using the Least Mean Square (LMS) Algorithm.'RLS'— Update the equalizer tap weights using the Recursive Least Square (RLS) Algorithm.'CMA'— Update the equalizer tap weights using the Constant Modulus Algorithm (CMA).
Data Types: char | string
Number of forward equalizer taps, specified as a positive integer. The number of
forward equalizer taps must be greater than or equal to the value of the InputSamplesPerSymbol property.
Data Types: double
Number of feedback equalizer taps, specified as a positive integer.
Data Types: double
Step size used by the adaptive algorithm, specified as a positive scalar. Increasing the step size reduces the equalizer convergence time but causes the equalizer output estimates to be less stable.
Tip
To determine the maximum step size allowed, use the maxstep
object function.
Tunable: Yes
Dependencies
To enable this property, set Algorithm
to 'LMS' or 'CMA'.
Data Types: double
Forgetting factor used by the adaptive algorithm, specified as a scalar in the range (0, 1]. Decreasing the forgetting factor reduces the equalizer convergence time but causes the equalizer output estimates to be less stable.
Tunable: Yes
Dependencies
To enable this property, set Algorithm
to 'RLS'.
Data Types: double
Initial inverse correlation matrix, specified as a scalar or an
NTaps-by-NTaps
matrix. NTaps is equal to the sum of the
NumForwardTaps and NumFeedbackTaps property values. If you specify
InitialInverseCorrelationMatrix as a scalar,
a, the equalizer sets the initial inverse correlation matrix to
a times the identity matrix:
a(eye(NTaps)).
Dependencies
To enable this property, set Algorithm
to 'RLS'.
Data Types: double
Signal constellation, specified as a vector. The default value is a QPSK
constellation generated using this code: pskmod(0:3,4,pi/4).
Data Types: double
Reference tap, specified as a positive integer less than or equal to the NumForwardTaps property value. The equalizer uses the reference tap location to track the main energy of the channel.
Data Types: double
Input signal delay in samples relative to the reset time of the equalizer, specified
as a nonnegative integer. If the input signal is a vector of length greater than 1, then
the input delay is relative to the start of the input vector. If the input signal is a
scalar, then the input delay is relative to the first call of the System object and to the first call of the System object after calling the release or reset object function.
Data Types: double
Number of input samples per symbol, specified as a positive integer. Setting this property to any number greater than one effectively creates a fractionally spaced equalizer.
Data Types: double
Enable training control input, specified as a logical 0
(false) or 1 (true). Setting
this property to true enables the equalizer training flag input
tf.
Data Types: logical
Update tap weights when not training, specified as a logical 1
(true) or 0 (false). If this
property is set to true, the System object uses decision directed mode to update equalizer tap weights. If this
property is set to false, the System object keeps the equalizer tap weights unchanged after training.
Data Types: logical
Source of adapt tap weights request, specified as one of these values:
'Property'— Specify this value to use the AdaptWeights property to control when the System object adapts tap weights.'Input port'— Specify this value to use theawinput to control when the System object adapts tap weights.
Dependencies
To enable this property, set Algorithm
to 'CMA'.
Data Types: char | string
Adapt tap weights, specified as a logical 1
(true) or 0 (false). If this
property is set to true, the System object updates the equalizer tap weights. If this property is set to
false, the System object keeps the equalizer tap weights unchanged.
Dependencies
To enable this property, set AdaptWeightsSource to 'Property' and set AdaptAfterTraining to true.
Data Types: logical
Source for initial tap weights, specified as one of these values:
'Auto'— Initialize the tap weights to the algorithm-specific default values, as described in the InitialWeights property.'Property'— Initialize the tap weights using the InitialWeights property value.
Data Types: char | string
Initial weights used by the adaptive algorithm, specified as a scalar or vector. The
default is 0 when the Algorithm
property is set to 'LMS' or 'RLS'. The default is
[0;0;1;0;0] when the Algorithm
property is set to 'CMA'.
If you specify InitialWeights as a scalar, the equalizer uses
scalar expansion to create a vector of length
NTaps with all values set to
InitialWeights. NTaps
is equal to the sum of the NumForwardTaps and NumFeedbackTaps property values. If you specify
InitialWeights as a vector, the vector length must be
NTaps.
Data Types: double
Tap weight update period in symbols, specified as a positive integer. The equalizer updates the tap weights after processing this number of symbols.
Data Types: double
Usage
Syntax
Description
Y = dfe(X,tsym,tf)tf. The System object starts training when tf changes from
false to true (at the rising edge). The
System object trains until all symbols in tsym are processed. The
input tsym is ignored when tf is
false. To enable this syntax, set the Algorithm
property to 'LMS' or 'RLS' and TrainingFlagInputPort property to true.
Y = dfe(X,aw)aw. If aw is
true, the System object adapts the equalizer tap weights. If aw is
false, the System object keeps the weights unchanged. To enable this syntax, set the Algorithm
property to 'CMA' and AdaptWeightsSource property to 'Input port'.
Input Arguments
Input signal, specified as a column vector. The input signal vector length must be equal to an integer multiple of the InputSamplesPerSymbol property value. For more information, see Symbol Tap Spacing.
This object accepts variable-size inputs. After the object is locked, you can change the size of each input channel, but you cannot change the number of channels. For more information, see Variable-Size Signal Support with System Objects.
Data Types: double
Complex Number Support: Yes
Training symbols, specified as a column vector of length less than or equal to the
length of input X. The input tsym is ignored
when tf is false.
Dependencies
To enable this argument, set the Algorithm
property to 'LMS' or 'RLS'.
Data Types: double
Training flag, specified as a logical 1
(true) or 0 (false). The
System object starts training when tf changes from
false to true (at the rising edge). The
System object trains until all symbols in tsym are processed. The
input tsym is ignored when tf is
false.
Dependencies
To enable this argument, set the Algorithm
property to 'LMS' or 'RLS' and TrainingFlagInputPort property to true.
Data Types: logical
Adapt weights flag, specified as a logical 1
(true) or 0 (false). If
aw is true, the System object adapts weights. If aw is false,
the System object keeps the weights unchanged.
Dependencies
To enable this argument, set the Algorithm
property to 'CMA' and AdaptWeightsSource property to 'Input port'.
Data Types: logical
Output Arguments
Equalized symbols, returned as a column vector that has the same length as input
signal X.
Error signal, returned as a column vector that has the same length as input signal
X.
Tap weights, returned as a column vector that has
NTaps elements.
NTaps is equal to the sum of the NumForwardTaps and NumFeedbackTaps property values. weights contains
the tap weights from the last tap weight update.
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
isLocked | Determine if System object is in use |
clone | Create duplicate System object |
info | Characteristic information about the equalizer object |
maxstep | Maximum step size for LMS equalizer convergence |
mmseweights | Linear equalizer MMSE tap weights |
Examples
Create an equalizer System object™, specifying a decision feedback LMS equalizer having eight forward taps, five feedback taps, a step size of 0.03, and expecting a BPSK signal constellation.
M = 2; % Modulation order eqdfe_lms = comm.DecisionFeedbackEqualizer(Algorithm='LMS', ... NumForwardTaps=8,NumFeedbackTaps=5,StepSize=0.03, ... Constellation=pskmod(0:M-1,M));
Change the reference tap index of the equalizer.
eqdfe_lms.ReferenceTap = 4;
Build a set of test data. Receive the data by convolving the signal.
x = pskmod(randi([0 M-1],1000,1),M); rxsig = conv(x,[1 0.8 0.3]);
Use maxstep to display the maximum permitted step size.
mxStep = maxstep(eqdfe_lms,rxsig)
mxStep = 0.1028
Equalize the received signal. Use the first 200 symbols as the training sequence.
y = eqdfe_lms(rxsig,x(1:200));
Apply decision feedback equalization using the least mean squares (LMS) algorithm to recover QPSK symbols passed through a delayed multipath AWGN channel.
Initialize simulation variables.
M = 4; % QPSK
numSymbols = 10000;
numTrainingSymbols = 1000;
chtaps = [1 0.5*exp(1i*pi/6) 0.1*exp(-1i*pi/8)];Generate QPSK-modulated symbols. Apply delayed multipath channel filtering and AWGN impairments to the symbols.
data = randi([0 M-1], numSymbols, 1);
tx = pskmod(data, M, pi/4);
rx = awgn(filter(chtaps,1,tx),25,'measured');Create a decision feedback equalizer System object and display the default configuration. Adjust the reference tap to 1. Check the maximum permitted step size. Equalize the impaired symbols.
eq = comm.DecisionFeedbackEqualizer
eq =
comm.DecisionFeedbackEqualizer with properties:
Algorithm: 'LMS'
NumForwardTaps: 5
NumFeedbackTaps: 3
StepSize: 0.0100
Constellation: [0.7071 + 0.7071i -0.7071 + 0.7071i -0.7071 - 0.7071i 0.7071 - 0.7071i]
ReferenceTap: 3
InputDelay: 0
InputSamplesPerSymbol: 1
TrainingFlagInputPort: false
AdaptAfterTraining: true
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
eq.ReferenceTap = 1; mxStep = maxstep(eq,rx)
mxStep = 0.2149
[y,err,weights] = eq(rx,tx(1:numTrainingSymbols));
Plot the constellation of the impaired and equalized symbols.
constell = comm.ConstellationDiagram('NumInputPorts',2);
constell(rx,y)
Plot the equalizer error signal and compute the error vector magnitude of the equalized symbols.
plot(abs(err)) grid on; xlabel('Symbols'); ylabel('|e|')
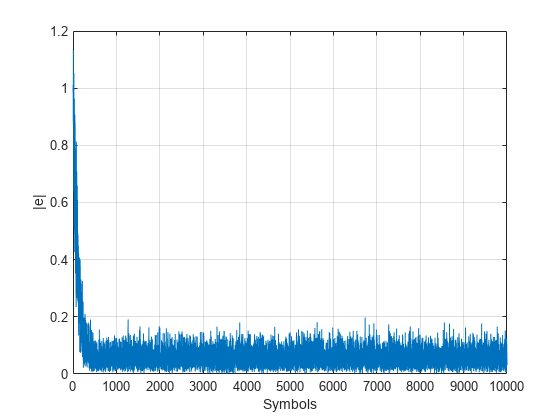
errevm = comm.EVM; evm = errevm(tx,y)
evm = 10.1268
Plot the equalizer tap weights.
subplot(3,1,1); stem(real(weights)); ylabel('real(weights)'); xlabel('Tap'); grid on; axis([1 8 -0.5 1]) line([eq.NumForwardTaps+0.5 eq.NumForwardTaps+0.5], ... [-0.5 1],'Color','r','LineWidth',1) title('Equalizer Tap Weights') subplot(3,1,2); stem(imag(weights)); ylabel('imag(weights)'); xlabel('Tap'); grid on; axis([1 8 -0.5 1]) line([eq.NumForwardTaps+0.5 eq.NumForwardTaps+0.5], ... [-0.5 1],'Color','r','LineWidth',1) subplot(3,1,3); stem(abs(weights)); ylabel('abs(weights)'); xlabel('Tap'); grid on; axis([1 8 -0.5 1]) line([eq.NumForwardTaps+0.5 eq.NumForwardTaps+0.5], ... [-0.5 1],'Color','r','LineWidth',1)

Demonstrate decision feedback equalization using the least mean squares (LMS) algorithm to recover QPSK symbols passed through an AWGN channel. Apply different equalizer training schemes and show the symbol error magnitude.
System Setup
Simulate a QPSK-modulated system subject to AWGN. Transmit packets composed of 200 training symbols and 1800 random data symbols. Configure a decision feedback LMS equalizer to recover the packet data.
M = 4; numTrainSymbols = 200; numDataSymbols = 1800; SNR = 20; trainingSymbols = ... pskmod(randi([0 M-1],numTrainSymbols,1),M,pi/4); numPkts = 10; dfeq = comm.DecisionFeedbackEqualizer( ... Algorithm="LMS", ... NumForwardTaps=5, ... NumFeedbackTaps=4, ... ReferenceTap=3, ... StepSize=0.01);
Train the Equalizer at the Beginning of Each Packet with Reset
Process each packet using prepended training symbols. Reset the equalizer after processing each packet. Resetting the equalizer after each packet forces the equalizer to train taps with no a priori knowledge. Equalizer error signal plots for the first, second, and last packet show higher symbol errors at the start of each packet.
jj = 1; figure for ii = 1:numPkts b = randi([0 M-1],numDataSymbols,1); dataSym = pskmod(b,M,pi/4); packet = [trainingSymbols;dataSym]; rx = awgn(packet,SNR); [~,err] = dfeq(rx,trainingSymbols); reset(dfeq) if (ii ==1 || ii == 2 ||ii == numPkts) subplot(3,1,jj) plot(abs(err)) ylim([0 1]) title(['Packet # ',num2str(ii)]) xlabel('Symbols'); ylabel('Error Magnitude'); grid on; jj = jj+1; end end

Train the Equalizer at the Beginning of Each Packet Without Reset
Process each packet using prepended training symbols. Do not reset the equalizer after each packet is processed. By not resetting after each packet, the equalizer retains tap weights from training prior packets. Equalizer error signal plots for the first, second, and last packet show that after the initial training on the first packet, subsequent packets have less symbol errors at the start of each packet.
release(dfeq) jj = 1; figure for ii = 1:numPkts b = randi([0 M-1],numDataSymbols,1); dataSym = pskmod(b,M,pi/4); packet = [trainingSymbols;dataSym]; channel = 1; rx = awgn(packet*channel,SNR); [~,err] = dfeq(rx,trainingSymbols); if (ii ==1 || ii == 2 ||ii == numPkts) subplot(3,1,jj) plot(abs(err)) ylim([0 1]) title(['Packet # ',num2str(ii)]) xlabel('Symbols'); ylabel('Error Magnitude'); grid on; jj = jj+1; end end

Train the Equalizer Periodically
Systems with signals subject to time-varying channels require periodic equalizer training to maintain lock on the channel variations. Specify a system that has 200 symbols of training for every 1800 data symbols. Between training, the equalizer does not update tap weights. The equalizer processes 200 symbols per packet.
Rs = 1e6;
fd = 20;
spp = 200; % Symbols per packet
b = randi([0 M-1],numDataSymbols,1);
dataSym = pskmod(b,M,pi/4);
packet = [trainingSymbols; dataSym];
stream = repmat(packet,10,1);
tx = (0:length(stream)-1)'/Rs;
channel = exp(1i*2*pi*fd*tx);
rx = awgn(stream.*channel,SNR);Set the AdaptAfterTraining property to false to stop the equalizer tap weight updates after the training phase.
release(dfeq) dfeq.AdaptAfterTraining = false
dfeq =
comm.DecisionFeedbackEqualizer with properties:
Algorithm: 'LMS'
NumForwardTaps: 5
NumFeedbackTaps: 4
StepSize: 0.0100
Constellation: [0.7071 + 0.7071i -0.7071 + 0.7071i -0.7071 - 0.7071i 0.7071 - 0.7071i]
ReferenceTap: 3
InputDelay: 0
InputSamplesPerSymbol: 1
TrainingFlagInputPort: false
AdaptAfterTraining: false
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
Equalize the impaired data. Plot the angular error from the channel, the equalizer error signal, and signal constellation. As the channel varies, the equalizer output does not remove the channel effects. Also, the output constellation rotates out of sync, resulting in bit errors.
[y,err] = dfeq(rx,trainingSymbols); figure subplot(2,1,1) plot(tx, unwrap(angle(channel))) xlabel('Time (sec)') ylabel('Channel Angle (rad)') title('Angular Error Over Time') subplot(2,1,2) plot(abs(err)) xlabel('Symbols') ylabel('Error Magnitude') grid on title('Time-Varying Channel Without Retraining')

scatterplot(y)

Set the TrainingInputPort property to true to configure the equalizer to retrain the taps when signaled by the trainFlag input. The equalizer trains only when trainFlag is true. After every 2000 symbols, the equalizer retrains the taps and keeps lock on variations of the channel. Plot the angular error from the channel, the equalizer error signal, and signal constellation. As the channel varies, the equalizer output removes the channel effects. Also, the output constellation does not rotate out of sync, and bit errors are reduced.
release(dfeq) dfeq.TrainingFlagInputPort = true; symbolCnt = 0; numPackets = length(rx)/spp; trainFlag = true; trainingPeriod = 2000; eVec = zeros(size(rx)); yVec = zeros(size(rx)); for p=1:numPackets [yVec((p-1)*spp+1:p*spp,1),eVec((p-1)*spp+1:p*spp,1)] = ... dfeq(rx((p-1)*spp+1:p*spp,1), ... trainingSymbols,trainFlag); symbolCnt = symbolCnt + spp; if symbolCnt >= trainingPeriod trainFlag = true; symbolCnt = 0; else trainFlag = false; end end figure subplot(2,1,1) plot(tx, unwrap(angle(channel))) xlabel('t (sec)') ylabel('Channel Angle (rad)') title('Angular Error Over Time') subplot(2,1,2) plot(abs(eVec)) xlabel('Symbols') ylabel('Error Magnitude') grid on title('Time-Varying Channel With Retraining')

scatterplot(yVec)

Simulate a system with delay between the transmitted symbols and received samples. Typical systems have transmitter and receiver filters that result in a delay. This delay must be accounted for to synchronize the system. In this example, the system delay is introduced without transmit and receive filters. Decision feedback equalization, using the least mean squares (LMS) algorithm, recovers QPSK symbols.
Initialize simulation variables.
M = 4; % QPSK
numSymbols = 10000;
numTrainingSymbols = 1000;
mpChan = [1 0.5*exp(1i*pi/6) 0.1*exp(-1i*pi/8)];
systemDelay = dsp.Delay(20);
snr = 24;Generate QPSK-modulated symbols. Apply multipath channel filtering, a system delay, and AWGN to the transmitted symbols.
data = randi([0 M-1],numSymbols,1); tx = pskmod(data,M,pi/4); % OQPSK delayedSym = systemDelay(filter(mpChan,1,tx)); rx = awgn(delayedSym,snr,'measured');
Create equalizer and EVM System objects. The equalizer System object specifies a decision feedback equalizer using the LMS algorithm.
dfeq = comm.DecisionFeedbackEqualizer('Algorithm','LMS', ... 'NumForwardTaps',9,'NumFeedbackTaps',6,'ReferenceTap',5); evm = comm.EVM('ReferenceSignalSource', ... 'Estimated from reference constellation');
Equalize Without Adjusting Input Delay
Equalize the received symbols.
[y1,err1,wts1] = dfeq(rx,tx(1:numTrainingSymbols,1));
Find the delay between the received symbols and the transmitted symbols by using the finddelay function.
rxDelay = finddelay(tx,rx)
rxDelay = 20
Display the equalizer information. The latency value indicates the delay introduced by the equalizer. Calculate the total delay as the sum of rxDelay and the equalizer latency.
eqInfo = info(dfeq)
eqInfo = struct with fields:
Latency: 4
totalDelay = rxDelay + eqInfo.Latency;
Until the equalizer output converges, the symbol error rate is high. Plot the error output, err1, to determine when the equalized output converges.
plot(abs(err1)) xlabel('Symbols') ylabel('Error Magnitude') title('Equalizer Error Signal')

The plot shows excessive errors for the first 2000 symbols. When demodulating symbols and computing symbol errors, account for the unconverged output and the system delay between the equalizer output and transmitted symbols.
dataRec1 = pskdemod(y1(2000+totalDelay:end),M,pi/4); symErrWithDelay = symerr(data(2000:end-totalDelay),dataRec1)
symErrWithDelay = 5977
evmWithDelay = evm(y1)
evmWithDelay = 26.3382
The error rate and EVM are high because the receive delay was not accounted for in the equalizer System object.
Adjust Input Delay in Decision Feedback Equalizer
Equalize the received data by using the delay value to set the InputDelay property. Since InputDelay is a nontunable property, you must release the dfeq System object to reconfigure the InputDelay property. Equalize the received symbols.
release(dfeq) dfeq.InputDelay = rxDelay
dfeq =
comm.DecisionFeedbackEqualizer with properties:
Algorithm: 'LMS'
NumForwardTaps: 9
NumFeedbackTaps: 6
StepSize: 0.0100
Constellation: [0.7071 + 0.7071i -0.7071 + 0.7071i -0.7071 - 0.7071i 0.7071 - 0.7071i]
ReferenceTap: 5
InputDelay: 20
InputSamplesPerSymbol: 1
TrainingFlagInputPort: false
AdaptAfterTraining: true
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
[y2,err2,wts2] = dfeq(rx,tx(1:numTrainingSymbols,1));
Plot the tap weights and equalized error magnitude. A stem plot shows the equalizer tap weights before and after the system delay is removed. A 2-D line plot shows the slower equalizer convergence for the delayed signal, as compared to the signal with the delay removed.
subplot(2,1,1) stem([real(wts1),real(wts2)]) xlabel('Taps') ylabel('Tap Weight Real') legend('rxDelayed','rxDelayRemoved') grid on subplot(2,1,2) stem([imag(wts1),imag(wts2)]) xlabel('Taps') ylabel('Tap Weight Imaginary') legend('rxDelayed','rxDelayRemoved') grid on

figure plot([abs(err1),abs(err2)]) xlabel('Symbols') ylabel('Error Magnitude') legend('rxDelayed','rxDelayRemoved') grid on
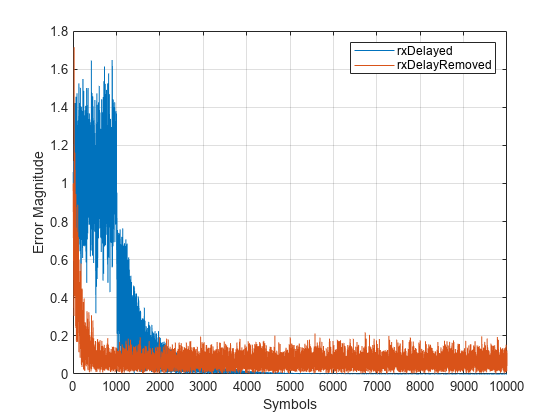
Plot error output of the equalized signals, rxDelayed and rxDelayRemoved. For the signal that has the delay removed, the equalizer converges during the 1000 symbol training period. When demodulating symbols and computing symbol errors, to account for the unconverged output and the system delay between the equalizer output and transmitted symbols, skip the first 500 symbols. Reconfiguring the equalizer to account for the system delay enables better equalization of the signal, and reduces symbol errors and the EVM.
eqInfo = info(dfeq)
eqInfo = struct with fields:
Latency: 4
totalDelay = rxDelay + eqInfo.Latency; dataRec2 = pskdemod(y2(500+totalDelay:end),M,pi/4); symErrDelayRemoved = symerr(data(500:end-totalDelay),dataRec2)
symErrDelayRemoved = 0
evmDelayRemoved = evm(y2(500+totalDelay:end))
evmDelayRemoved = 7.5357
Recover QPSK symbols with a decision equalizer, using the constant modulus algorithm (CMA) and EVM-based taps training. When using blind equalizer algorithms, such as CMA, you can train the equalizer taps using the AdaptWeights property to start and stop training. Use helper functions to generate plots and apply phase correction.
Initialize system variables.
rng(123456); M = 4; % QPSK numSymbols = 100; numPackets = 5000; refTap = 3; nFwdTaps = 5; nFdbkTaps = 4; ttlTaps = nFwdTaps + nFdbkTaps; raylChan = comm.RayleighChannel( ... 'PathDelays',[0 1], ... 'AveragePathGains',[0 -12], ... 'MaximumDopplerShift',1e-5); SNR = 50; adaptWeights = true;
Create the equalizer and EVM System objects. The equalizer System object specifies a decision feedback equalizer using the CMA adaptive algorithm. Call the helper function to initialize figure plots.
dfeq = comm.DecisionFeedbackEqualizer( ... 'Algorithm','CMA', ... 'NumForwardTaps',nFwdTaps, ... 'NumFeedbackTaps',nFdbkTaps, ... 'ReferenceTap',refTap, ... 'StepSize',0.03, ... 'AdaptWeightsSource','Input port')
dfeq =
comm.DecisionFeedbackEqualizer with properties:
Algorithm: 'CMA'
NumForwardTaps: 5
NumFeedbackTaps: 4
StepSize: 0.0300
Constellation: [0.7071 + 0.7071i -0.7071 + 0.7071i -0.7071 - 0.7071i 0.7071 - 0.7071i]
ReferenceTap: 3
InputSamplesPerSymbol: 1
AdaptWeightsSource: 'Input port'
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
info(dfeq)
ans = struct with fields:
Latency: 2
evm = comm.EVM('ReferenceSignalSource', ... 'Estimated from reference constellation'); [errPlot,evmPlot,scatSym,adaptState] = ... initFigures(numPackets,ttlTaps);
Equalization Loop
Follow these steps to implement the equalization loop.
Generate OQPSK data packets.
Apply Rayleigh fading and AWGN to the transmission data.
Apply equalization to the received data and phase correction to the equalizer output.
Estimate the EVM and toggle the
adaptWeightsflag totrueorfalsebased on the EVM level.Update the figure plots.
for p=1:numPackets data = randi([0 M-1],numSymbols,1); tx = pskmod(data,M,pi/4); rx = awgn(raylChan(tx),SNR); rxDelay = finddelay(rx,tx); [y,err,wts] = dfeq(rx,adaptWeights); y = phaseCorrection(y); evmEst = evm(y); adaptWeights = (evmEst > 20); updateFigures(errPlot,evmPlot,scatSym,adaptState, ... wts,y(end),evmEst,adaptWeights,p,numPackets) end

rxDelay
rxDelay = 0
The figure plots show that, as the EVM varies, the equalizer toggles in and out of decision-directed weight adaptation mode.
Helper Functions
This helper function initializes figures that show a quad plot of simulation results.
function [errPlot,evmPlot,scatter,adaptState] = ... initFigures(numPkts,ttlTaps) yVec = nan(numPkts,1); evmVec = nan(numPkts,1); wVec = zeros(ttlTaps,1); adaptVec = nan(numPkts,1); figure subplot(2,2,1) evmPlot = stem(wVec); grid on; axis([1 ttlTaps 0 1.8]) xlabel('Taps'); ylabel('|Weights|'); title('Tap Weight Magnitude') subplot(2,2,2) scatter = plot(yVec, '.'); axis square; axis([-1.2 1.2 -1.2 1.2]); grid on; xlabel('In-phase'); ylabel('Quadrature'); title('Scatter Plot'); subplot(2,2,3) adaptState = plot(adaptVec); grid on; axis([0 numPkts -0.2 1.2]) ylabel('Training'); xlabel('Symbols'); title('Adapt Weights Signal') subplot(2,2,4) errPlot = plot(evmVec); grid on; axis([1 numPkts 0 100]) xlabel('Symbols'); ylabel('EVM (%)'); title('EVM') end
This helper function updates the figures.
function updateFigures(errPlot,evmPlot,scatSym, ... adaptState,w,y,evmEst,adaptWts,p,numFrames) persistent yVec evmVec adaptVec if p == 1 yVec = nan(numFrames,1); evmVec = nan(numFrames,1); adaptVec = nan(numFrames,1); end yVec(p) = y; evmVec(p) = evmEst; adaptVec(p) = adaptWts; errPlot.YData = abs(evmVec); evmPlot.YData = abs(w); scatSym.XData = real(yVec); scatSym.YData = imag(yVec); adaptState.YData = adaptVec; drawnow limitrate end
This helper function applies phase correction.
function y = phaseCorrection(y) a = angle(y((real(y) > 0) & (imag(y) > 0))); a(a < 0.1) = a(a < 0.1) + pi/2; theta = mean(a) - pi/4; y = y * exp(-1i*theta); end
Recover QPSK symbols in fading environments with a decision feedback equalizer, using the least mean squares (LMS) algorithm. Use the reset object function to equalize independent packets. Use helper functions to generate plots. This example also shows symbol-based processing and frame-based processing.
Setup
Initialize system variables, create the equalizer System object, and initialize the plot figures.
M = 4; % QPSK numSym = 1000; numTrainingSym = 100; numPackets = 5; refTap = 5; nFwdTaps = 9; nFdbkTaps = 4; ttlTaps = nFwdTaps + nFdbkTaps; stepsz = 0.01; ttlNumSym = numSym + numTrainingSym; raylChan = comm.RayleighChannel( ... 'PathDelays',[0 1], ... 'AveragePathGains',[0 -9], ... 'MaximumDopplerShift',0, ... 'PathGainsOutputPort',true); SNR = 35; rxVec = zeros(ttlNumSym,numPackets); txVec = zeros(ttlNumSym,numPackets); yVec = zeros(ttlNumSym,1); eVec = zeros(ttlNumSym,1); dfeq1 = comm.DecisionFeedbackEqualizer( ... 'Algorithm','LMS', ... 'NumForwardTaps',nFwdTaps, ... 'NumFeedbackTaps',nFdbkTaps, ... 'ReferenceTap',refTap, ... 'StepSize',stepsz, ... 'TrainingFlagInputPort',true); [errPlot,wStem,hStem,scatPlot] = ... initFigures(ttlNumSym,ttlTaps, ... raylChan.AveragePathGains);
Symbol-Based Processing
For symbol-based processing, provide one symbol at the input of the equalizer. Reset the equalizer state and channel after processing each packet.
for p = 1:numPackets trainingFlag = true; for q=1:ttlNumSym data = randi([0 M-1],1,1); tx = pskmod(data,M,pi/4); [xc,pg] = raylChan(tx); rx = awgn(xc,25); [y,err,wts] = dfeq1(rx,tx,trainingFlag);
Disable training after processing numTrainingSym training symbols.
if q == numTrainingSym trainingFlag = false; end updateFigures(errPlot,wStem,hStem, ... scatPlot,err,wts,y,pg,q,ttlNumSym); txVec(q,p) = tx; rxVec(q,p) = rx; end
After processing each packet, reset the channel System object to get a new realization of channel taps and the equalizer System object to restore the default taps weights.
reset(raylChan)
reset(dfeq1)
end
Packet-Based Processing
For packet-based processing, provide one packet at the input of the equalizer. Each packet contains ttlNumSym symbols. Because the training duration is less than the packet length, you do not need to specify the start-training input.
yVecPkt = zeros(ttlNumSym,numPackets); errVecPkt = zeros(ttlNumSym,numPackets); wgtVecPkt = zeros(ttlTaps,numPackets); dfeq2 = comm.DecisionFeedbackEqualizer( ... 'Algorithm','LMS', ... 'NumForwardTaps',nFwdTaps, ... 'NumFeedbackTaps',nFdbkTaps, ... 'ReferenceTap',refTap, ... 'StepSize',stepsz); for p = 1:numPackets [yVecPkt(:,p),errVecPkt(:,p),wgtVecPkt(:,p)] = ... dfeq2(rxVec(:,p),txVec(1:numTrainingSym,p)); for q=1:ttlNumSym updateFigures(errPlot,wStem,hStem,scatPlot, ... errVecPkt(q,p),wgtVecPkt(:,p),yVecPkt(q,p), ... pg,q,ttlNumSym); end
After processing each packet, reset the channel System object to get a new realization of channel taps and the equalizer System object to restore the default taps weights.
reset(raylChan)
reset(dfeq2)
end
Helper Functions
This helper function initializes the figures.
function [errPlot,wStem,hStem,scatPlot] = ... initFigures(ttlNumSym,ttlTap,pg) yVec = nan(ttlNumSym,1); eVec = nan(ttlNumSym,1); wVec = zeros(ttlTap,1); figure; subplot(2,2,1); wStem = stem(wVec); axis([1 ttlTap 0 1.8]); grid on; xlabel('Taps'); ylabel('|Weights|'); title('Tap Weight Magnitude') subplot(2,2,2); hStem = stem([0 abs(pg) 0]); grid on; xlabel('Taps'); ylabel('|Path Gain|'); title('Channel Path Gain Magnitude') subplot(2,2,3); errPlot = plot(eVec); axis([1 ttlNumSym 0 1.2]); grid on xlabel('Symbols'); ylabel('|Error Magnitude|'); title('Error Magnitude') subplot(2,2,4); scatPlot = plot(yVec,'.'); axis square; axis([-1.2 1.2 -1.2 1.2]); grid on; xlabel('In-phase'); ylabel('Quadrature'); title(sprintf('Scatter Plot')); end
This helper function updates the figures.
function updateFigures(errPlot,wStem,hStem,scatPlot, ... err,wts,y,pg,p,ttlNumSym) persistent yVec eVec if p == 1 yVec = nan(ttlNumSym,1); eVec = nan(ttlNumSym,1); end yVec(p) = y; eVec(p) = abs(err); errPlot.YData = abs(eVec); wStem.YData = abs(wts); hStem.YData = [0 abs(pg) 0]; scatPlot.XData = real(yVec); scatPlot.YData = imag(yVec); drawnow limitrate end
More About
You can configure the equalizer to operate as a symbol-spaced equalizer or as a fractional symbol-spaced equalizer.
To operate the equalizer at a symbol-spaced rate, specify the number of samples per symbol as
1. Symbol-rate equalizers have taps spaced at the symbol duration. Symbol-rate equalizers are sensitive to timing phase.To operate the equalizer at a fractional symbol-spaced rate, specify the number of input samples per symbol as an integer greater than
1and provide an input signal oversampled at that sampling rate. Fractional symbol-spaced equalizers have taps spaced at an integer fraction of the input symbol duration. Fractional symbol-spaced equalizers are not sensitive to timing phase.
Algorithms
A decision feedback equalizer (DFE) is a nonlinear equalizer that reduces intersymbol interference (ISI) in frequency-selective channels. If a null exists in the frequency response of a channel, DFEs do not enhance the noise. A DFE consists of a tapped delay line that stores samples from the input signal and contains a forward filter and a feedback filter. The forward filter is similar to a linear equalizer. The feedback filter contains a tapped delay line whose inputs are the decisions made on the equalized signal. Once per symbol period, the equalizer outputs a weighted sum of the values in the delay line and updates the weights to prepare for the next symbol period.
DFEs can be symbol-spaced or fractional symbol-spaced.
For a symbol-spaced equalizer, the number of samples per symbol, K, is 1. The output sample rate equals the input sample rate.
For a fractional symbol-spaced equalizer, the number of samples per symbol, K, is an integer greater than 1. Typically, K is 4 for fractional symbol-spaced equalizers. The output sample rate is 1/T and the input sample rate is K/T. Tap weight updating occurs at the output rate.
This schematic shows a fractional symbol-spaced DFE with a total of N weights, a symbol period of T, and K samples per symbol. The filter has L forward weights and N-L feedback weights. The forward filter is at the top, and the feedback filter is at the bottom. If K is 1, the result is a symbol-spaced DFE instead of a fractional symbol-spaced DFE.

In each symbol period, the equalizer receives K input samples at the forward filter and one decision or training sample at the feedback filter. The equalizer then outputs a weighted sum of the values in the forward and feedback delay lines and updates the weights to prepare for the next symbol period.
Note
The algorithm for the Adaptive Algorithm block in the schematic jointly optimizes the forward and feedback weights. Joint optimization is especially important for convergence in the recursive least square (RLS) algorithm.
For more information, see Equalization.
For the LMS algorithm, in the previous schematic, w is a vector of all weights wi, and u is a vector of all inputs ui. Based on the current set of weights, the LMS algorithm creates the new set of weights as
wnew = wcurrent + (StepSize) ue*.
The step size used by the adaptive algorithm is specified as a positive scalar. Increasing the
step size reduces the equalizer convergence time but causes the equalized output signal to
be less stable. To determine the maximum step size allowed when using the LMS adaptive
algorithm, use the maxstep object
function. The * operator denotes the complex conjugate and the error calculation e = d -
y.
For the RLS algorithm, in the previous schematic, w is the vector of all weights wi, and u is the vector of all inputs ui. Based on the current set of inputs, u, and the inverse correlation matrix, P, the RLS algorithm first computes the Kalman gain vector, K, as
The forgetting factor used by the adaptive algorithm is specified as a scalar in the range (0, 1]. Decreasing the forgetting factor reduces the equalizer convergence time but causes the equalized output signal to be less stable. H denotes the Hermitian transpose. Based on the current inverse correlation matrix, the new inverse correlation matrix is
Based on the current set of weights, the RLS algorithm creates the new set of weights as
wnew = wcurrent+K*e.
The * operator denotes the complex conjugate and the error calculation e = d - y.
For the CMA adaptive algorithm, in the previous schematic, w is the vector of all weights wi, and u is the vector of all inputs ui. Based on the current set of weights, the CMA adaptive algorithm creates the new set of weights as
wnew = wcurrent + (StepSize) u*e.
The step size used by the adaptive algorithm is specified as a positive scalar. Increasing the
step size reduces the equalizer convergence time but causes the equalized output signal to
be less stable. To determine the maximum step size allowed by the CMA adaptive algorithm,
use the maxstep object
function. The * operator denotes the complex conjugate and the error calculation
e = y(R -
|y|2), where R is a constant related to the signal
constellation.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Version History
Introduced in R2019a
See Also
Objects
Blocks
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Website auswählen
Wählen Sie eine Website aus, um übersetzte Inhalte (sofern verfügbar) sowie lokale Veranstaltungen und Angebote anzuzeigen. Auf der Grundlage Ihres Standorts empfehlen wir Ihnen die folgende Auswahl: .
Sie können auch eine Website aus der folgenden Liste auswählen:
So erhalten Sie die bestmögliche Leistung auf der Website
Wählen Sie für die bestmögliche Website-Leistung die Website für China (auf Chinesisch oder Englisch). Andere landesspezifische Websites von MathWorks sind für Besuche von Ihrem Standort aus nicht optimiert.
Amerika
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)