KeplerMinMax
KeplerMinMax
A novel closed-form solution to compute the surface altitude extrema for any two-body orbit is extended to oblate spheroids using Halley's method (a root finding technique with cubic convergence). Runtime performance has improved between three and five orders of magnitude while maintaining solution accuracy within several centimeters of numerically computed extrema when comparing this routine to conventional numerical minimization techniques such as fminbnd. This method is simple to port to flight hardware, requires little computational overhead, few lines of code, and a small memory footprint.
This repository contains a C code implementation of keplerMinMax as outlined in the 2021 AMOS conference paper titled "Novel Closed Form Solution for Orbit Segment Altitude Extrema Over Spherical and Oblate Central Bodies", it also has a MATLAB-C wrapper which allows for calling in a MATLAB environment. To compile a C MEX file in your MATLAB environment, execute the following command in your MATLAB command window:
>> mex keplerMinMaxMex.c keplerMinMax.c
The MATLAB MEX adapter, keplerMinMaxAdapter.m, is the MATLAB interface routine for keplerMinMax where it can be invoked by
[minAlt,maxAlt] = keplerMinMaxAdapter(r0,v0,rf,vf,tf,params,dim3);
r0 is an N-Dimensional position state vector, and its dimensions must be identical to those of v0, rf, and vf. The singleton dimension specifier, dim3, indicates which dimension corresponds to [x,y,z], tf must have identical dimensions to r0, v0, rf, vf except for it's singleton dimension which should be unity instead of three.
Once the C code is compiled into a MEX file, run the demo script to verify the configuration
>> keplerMinMaxDemo();
The runtime performance of keplerMinMax as well as fminbnd should be printed to the MATLAB Comand Window similar to
>> keplerMinMaxDemo:: keplerMinMax Execution Time = 0.038463 [s]
>> keplerMinMaxDemo:: fminbnd Execution Time = 66.5425 [s]
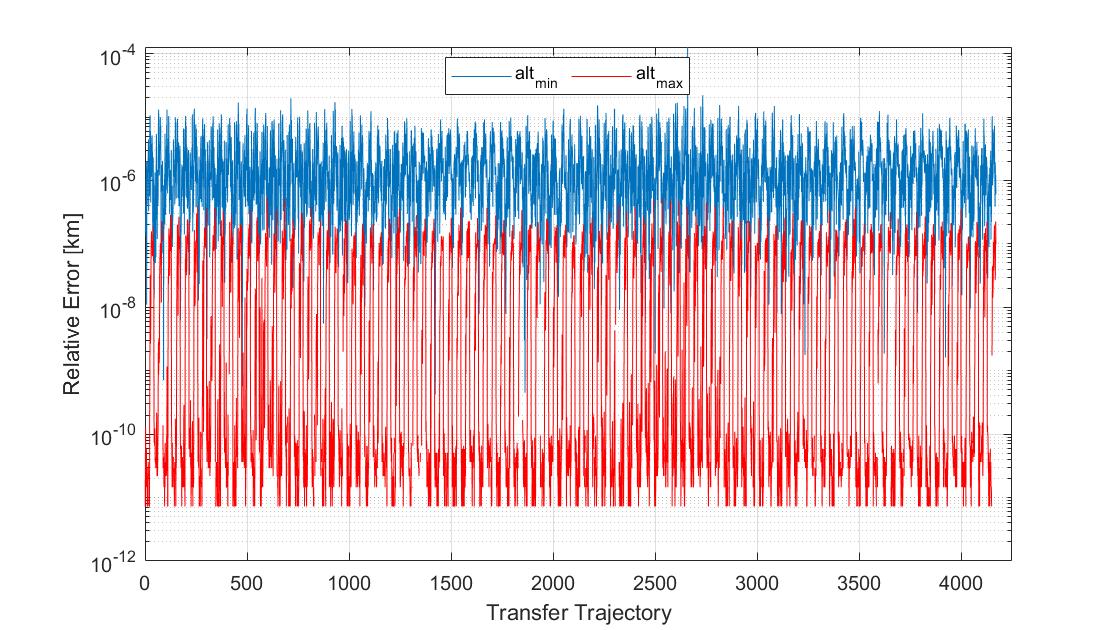
Next, a relative position error plot is displayed with the absolute difference in altitude minima and maxima values between implementations as shown below
The C routine is direclty accessible and included in keplerMinMax.c for inline function calls via
keplerMinMax(r0, v0, rf, vf, tf, mu, Re, Rp, Npts, minAlt, maxAlt);
A preliminary check on the equatorial and polar radius of the spheroid is performed internally; if Re = Rp, then an internal function call to keplerMinMaxSphere is made to save computational overhead. If desired, a direct call to the spherical altitude routine, keplerMinMaxSphere, can be performed as follows
keplerMinMaxSphere(r0, v0, rf, vf, tf, mu, R, minAlt, maxAlt);
where R is the spherical radius of the central body, mu is the standard gravitaional parameter, and the other inputs/outputs are in the same format and size as specified by keplerMinMax.
References:
Koblick, Darin C. "Novel Closed Form Solution for Orbit Segment Altitude Extrema Over Spherical and Oblate Central Bodies." AMOS 2021 (2021): 10.
Zitieren als
Darin Koblick (2025). KeplerMinMax (https://github.com/koblick/KeplerMinMax/releases/tag/v1.2), GitHub. Abgerufen.
Koblick, Darin C. "Novel Closed Form Solution for Orbit Segment Altitude Extrema Over Spherical and Oblate Central Bodies." AMOS 2021 (2021): 10.
Kompatibilität der MATLAB-Version
Plattform-Kompatibilität
Windows macOS LinuxTags
Quellenangaben
Inspiriert von: Flatten Any Mulitdimensional Matrix into a 2-D Matrix!
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Live Editor erkunden
Erstellen Sie Skripte mit Code, Ausgabe und formatiertem Text in einem einzigen ausführbaren Dokument.
| Version | Veröffentlicht | Versionshinweise | |
|---|---|---|---|
| 1.2 | See release notes for this release on GitHub: https://github.com/koblick/KeplerMinMax/releases/tag/v1.2 |