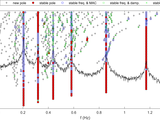
Operational modal analysis with automated SSI-COV algorithm
The modal parameters of a line-like structure are automatically identified using an SSI-COV algorithm applied to ambient vibration data
The function SSICOV.m aims to automatically identify the eigenfrequencies, mode shapes and damping ratios of a line-like structure using ambient vibrations only. The covariance-driven stochastic subspace identification method (SSI-COV) is used in combination with a clustering algorithm to automatically analyse the stabilization diagrams.
The algorithm is inspired by the one used by Magalhaes et al. [1]. It has been applied for ambient vibration monitoring of the Lysefjord Bridge [2] and was compared to the frequency domain decomposition technique [3]. Finally, the algorithm was found accurate enough to visualise the evolution of the bridge eigenfrequencies with the temperature [4].
The submission file contains:
- A data file BridgeData.mat
- A Matlab Live Script Example1.mlx that illustrates the application of the algorithm.
- A Matlab Live Script Example1_noToolbox.mlx that reproduce Example1 but using the function SSICOV_noToolbox.
- The function SSICOV which is the automated SSI-COV algorithm.
- The function SSICOV_noToolbox which is the automated SSI-COV algorithm but does not use the Statistics and Machine Learning Toolbox. The Linkage algorithm is replaced by the function "PHA_Clustering" by [5] and the function "cluster" is replaced by the function "Cluster2", which is derived from [6].
- The function plotStabDiag.m, which plot the stabilization diagram.
Any question, suggestion or comment is welcomed.
[1] Magalhaes, F., Cunha, A., & Caetano, E. (2009). Online automatic identification of the modal parameters of a long span arch bridge. Mechanical Systems and Signal Processing, 23(2), 316-329.
[2] Cheynet, E., Jakobsen, J. B., & Snæbjörnsson, J. (2016).Buffeting response of a suspension bridge in complex terrain. Engineering Structures, 128, 474-487.
[3] Cheynet, E., Jakobsen, J. B., & Snæbjörnsson, J. (2017).Damping estimation of large wind-sensitive structures.Procedia Engineering, 199, 2047-2053.
[4] Cheynet, E., Snæbjörnsson, J., & Jakobsen, J. B. (2017).Temperature Effects on the Modal Properties of a Suspension Bridge.In Dynamics of Civil Structures, Volume 2 (pp. 87-93). Springer.
[5] Yonggang (2021). Fast hierarchical clustering method - PHA (https://www.mathworks.com/matlabcentral/fileexchange/46134-fast-hierarchical-clustering-method-pha), MATLAB Central File Exchange. Retrieved February 4, 2021.
[6] Eric Ogier (2021). Hierarchical clustering (https://www.mathworks.com/matlabcentral/fileexchange/56844-hierarchical-clustering), MATLAB Central File Exchange. Retrieved February 4, 2021.
Zitieren als
Cheynet, E. Operational Modal Analysis with Automated SSI-COV Algorithm. Zenodo, 2020, doi:10.5281/ZENODO.3774061.
Kompatibilität der MATLAB-Version
Plattform-Kompatibilität
Windows macOS LinuxKategorien
- MATLAB > Mathematics > Numerical Integration and Differential Equations >
- Signal Processing > Signal Processing Toolbox > Vibration Analysis >
- Engineering > Mechanical Engineering > Acoustics, Noise and Vibration >
Tags
Quellenangaben
Inspiriert von: Hierarchical clustering, Fast hierarchical clustering method - PHA
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Live Editor erkunden
Erstellen Sie Skripte mit Code, Ausgabe und formatiertem Text in einem einzigen ausführbaren Dokument.
Versionen, die den GitHub-Standardzweig verwenden, können nicht heruntergeladen werden
| Version | Veröffentlicht | Versionshinweise | |
|---|---|---|---|
| 2.5 | See release notes for this release on GitHub: https://github.com/ECheynet/SSICOV/releases/tag/2.5 |
||
| 2.4 | See release notes for this release on GitHub: https://github.com/ECheynet/SSICOV/releases/tag/v2.4 |
||
| 2.3 | See release notes for this release on GitHub: https://github.com/ECheynet/SSICOV/releases/tag/v2.3 |
||
| 2.2 | Added Github repository |
|
|
| 2.1 | typos corrected + minor modification to improve the performances |
||
| 2.0.2 | typo |
||
| 2.0.1 | Set the default value of Ts as 500*dt instead of 20 s to avoid the crashing problem of Matlab if a very high sampling frequency is used. Ideally, Ts should be between two and six times the value of the lowest eigenfrequency of the system. |
||
| 2.0.0 | The distance parameter "pos" for the clustering algorithm is now properly defined using both the difference in terms of frequencies and the MAC number (thank Mihhail Samusev for the help!). Finally, the description of the submission is updated. |
||
| 1.0.4 | Updated the definition for the variable "pos" (Cluster analysis) + The default value for the time lag (cross-covariance) is more robustly defined + the variable T1 is preallocated |
||
| 1.0.3 | Description |
||
| 1.0.2 | Updated description |
||
| 1.0.1 | typo |
||
| 1.0.0 |