Simple Heat Equation solver
Finite differences for the 2D heat equation
Implementation of a simple numerical schemes for the heat equation.
Applying the second-order centered differences to approximate the spatial derivatives,
Neumann boundary condition is employed for no-heat flux, thus please note that the grid location is staggered. Once the right hand side is obtained, the equation can be solved by the ODE suite. Here we use ode15s. Copyright 2015-2016 The MathWorks, Inc.
Problem Setup
N = 50; % Number of grid in x,y-direction
L = 4*pi; % Domain size
% Grid point
x = linspace(0,L,N);
y = linspace(0,L,N);
% Make it staggered.
x = (x(1:end-1)+x(2:end))/2;
y = (y(1:end-1)+y(2:end))/2;
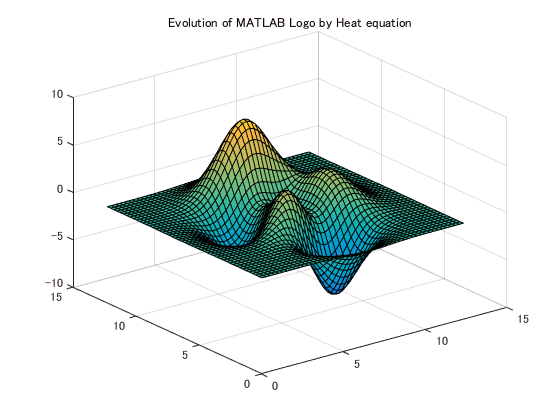
[X,Y] = meshgrid(x,y);Initial Condition
% Let's use MATLAB logo.
% A variable u0 is defined at the center of each grid cell
% thus the number of grid point is N-1.
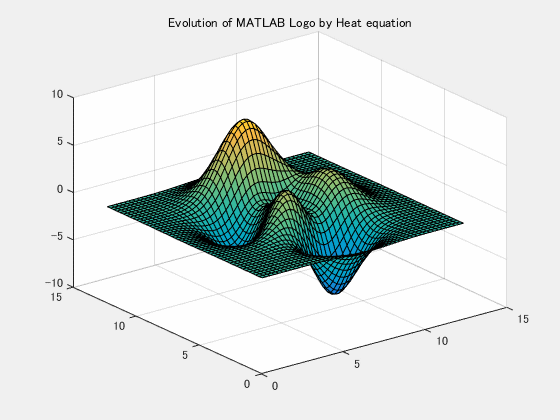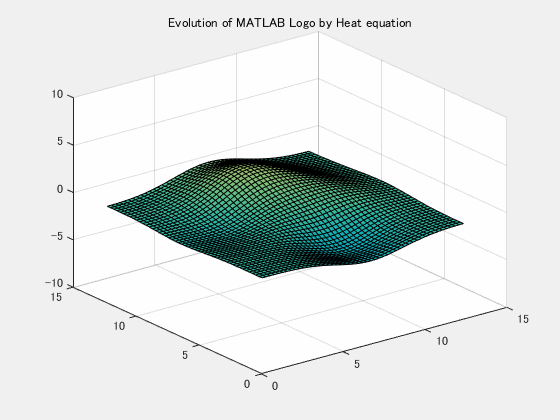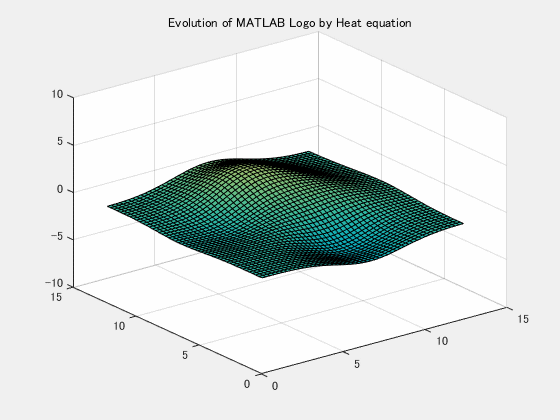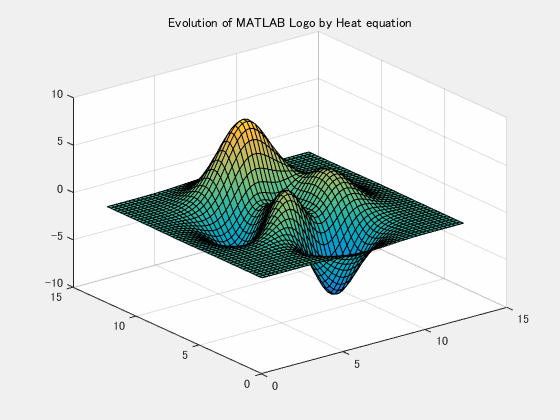
u0(:,:) = peaks(N-1);
% Plot it
handle_surf = surf(X,Y,u0);
handle_axes = gca;
handle_axes.ZLim = [-10,10];
handle_axes.CLim = [-10,10];
title('Evolution of MATLAB Logo by Heat equation');Simulation
dx = x(2)-x(1); % spatial grid size
alpha = 2; % coefficient
tspan = linspace(0,1,40);
[t,u] = ode15s(@(t,x)getRHS(x,alpha,dx,N),tspan,u0(:));Visualize
Tn = length(t);
u = reshape(u,Tn,N-1,N-1);
filename = 'heat.gif';
for ii=1:Tn
Z = u(ii,:,:);
Z = squeeze(Z);
handle_surf.ZData = Z;
drawnow;
frame = getframe(gcf);
im = frame2im(frame);
[A,map] = rgb2ind(im,256);
if ii==1
imwrite(A,map,filename,'gif','LoopCount',Inf,'DelayTime',0.05);
else
imwrite(A,map,filename,'gif','WriteMode','append','DelayTime',0.05);
end
endZitieren als
michio (2025). Simple Heat Equation solver (https://github.com/mathworks/Simple-Heat-Equation-solver), GitHub. Abgerufen.
Kompatibilität der MATLAB-Version
Plattform-Kompatibilität
Windows macOS LinuxKategorien
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Live Editor erkunden
Erstellen Sie Skripte mit Code, Ausgabe und formatiertem Text in einem einzigen ausführbaren Dokument.
Versionen, die den GitHub-Standardzweig verwenden, können nicht heruntergeladen werden
| Version | Veröffentlicht | Versionshinweise | |
|---|---|---|---|
| 1.0.0.3 | reflect markdown on File Exchange |
|
|
| 1.0.0.2 | Move to GitHub |
|
|
| 1.0.0.1 | Added a screenshot |
||
| 1.0.0.0 |