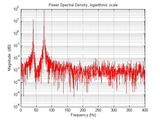
PSD (Power Spectral Density), and Amplitude Spectrum with adjusted FFT
Function [fy]=FFT(y,Fs)
1)computes the Power spectral density and Amplitude spectrum (P(f),F(f))
of 1d signal y(t) with sample rate Fs (Nyquist rate) which is known% apriori. The results are plotted in 3 figures which correspond to simple
PSD,logarithmic PSD (dB) and Amplitude Specturm respectively.
_____________
Ampitude(f) = \/ PSD(f)
2)The usefulness of this function is the adjustment of the frequency axis.
3)The fast Fourier transform is computed with Matlab built-in function
fft, but for signals whose lengths <1000 points, one can use the nested
function y=Fast_Fourier_Transform(X,N) .
Demo :
Fs=800;
Tf=2;
t=0:1/Fs:Tf;
f=[40 75];
Amp=[4.5 9.22];
sigma=1.33;
y=Amp(1)*exp(j*2*pi*t*f(1))
+Amp(2)*exp(j*2*pi*t*f(2));
N=(sigma/sqrt(2))* (randn(size(t))+j*randn(size(t)));
y=y+N;
figure, plot(t,y),xlabel('time (s)'),ylabel('Voltage (v)'),
title(strcat('Signal corrupted with AWGN, \sigma=',num2str(sigma))),
fy=FFT(y,Fs);
in the M-file Demo_FFT:
1st Part : we compute the spectrum of sinusoidal signal Y(t) with frequency Fc
2nd Part : FFT[Y²(t)]
The demo is adjusted with sample rate Fs>=4*Fc.
Zitieren als
Youssef Khmou (2024). PSD (Power Spectral Density), and Amplitude Spectrum with adjusted FFT (https://www.mathworks.com/matlabcentral/fileexchange/40002-psd-power-spectral-density-and-amplitude-spectrum-with-adjusted-fft), MATLAB Central File Exchange. Abgerufen.
Kompatibilität der MATLAB-Version
Plattform-Kompatibilität
Windows macOS LinuxKategorien
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Live Editor erkunden
Erstellen Sie Skripte mit Code, Ausgabe und formatiertem Text in einem einzigen ausführbaren Dokument.
| Version | Veröffentlicht | Versionshinweise | |
|---|---|---|---|
| 1.3.0.0 | errata : figure 2 is changed from semilogy(Frequency, Power) to 10*log10(Frequency, 10*log10(Power)) in Decibel . |
||
| 1.0.0.0 |