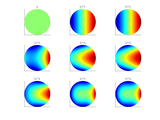
Zernike decomposition

Version 1.0.0.0 (845 Bytes) von Alex Chtchetinine
Decomposition of a 2-D function by set of Zernike functions
4.7
(7)
6,2K Downloads
Aktualisiert 10. Dez 2007

Keine Lizenz

This code was written to deal with "Zernike polynomials" code graciously donated by Paul Fricker via file exchange.
Here you will find a practical example of a function decomposition by
Zernike basis.
The function is F below, feel free to modify
Unlike Paul's example found in 'zernfun2.m' here the domain is the true unit circle, without NaN's filling it up to the unit square.
You will have to download Paul's functions to run this code.

Zitieren als

Alex Chtchetinine (2024). Zernike decomposition (https://www.mathworks.com/matlabcentral/fileexchange/17950-zernike-decomposition), MATLAB Central File Exchange. Abgerufen.

Kompatibilität der MATLAB-Version
Erstellt mit R2007b
Kompatibel mit allen Versionen
Plattform-Kompatibilität
Windows macOS Linux
Kategorien
Mehr zu Zernike Polynomials finden Sie in Help Center und MATLAB Answers
Quellenangaben

Inspiriert von: Zernike polynomials

Community Treasure Hunt

Find the treasures in MATLAB Central and discover how the community can help you!

Start Hunting!

Version Veröffentlicht Versionshinweise
1.0.0.0