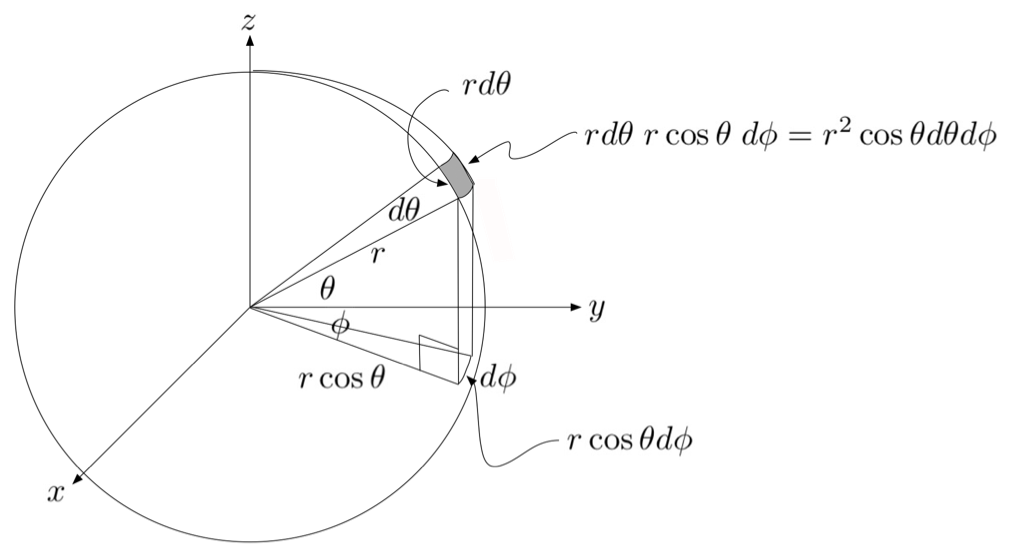
numerical double integral of an expression with vector defined variables
4 Ansichten (letzte 30 Tage)
Ältere Kommentare anzeigen
Hi everyone,
I have to compute double integral for the expression G over phi and theta in the following code numerically. Does anyone have any idea how it must be done, since it is not easy to use trapz or integral2 because of the definition of the variables!
c = 4.2;
d = 10;
r3 = linspace(c, d, 100);
theta = linspace(-pi/2, pi/2, 100);
theta2 = linspace(-pi/2 ,pi/2, 100);
Phi = linspace(0, 2*pi, 100);
Phi2 = linspace(0, 2*pi, 100);
G = r3.*(sin(theta2).*cos(theta).*cos(phi2-phi) - cos(theta2).*sin(theta)) ./(r3.^2 + c.^2 - 2.*r3.*c.*(sin(theta2).*sin(theta).*cos(phi2-phi)+cos(theta2).*cos(theta))).^3/2 ;
0 Kommentare
Akzeptierte Antwort
darova
am 9 Apr. 2020
Here is a start
phi = linspace(...) % define value for phi
theta = linspace(...); % define theta
dphi = phi(2)-phi(1); % phi step
dtheta = theta(2)-theta(1); % theta step
[PHI,THETA] = meshgrid(phi,theta); % create 2D grid
G = PHI .. THETA ... % calculate G at each point of grid
F = G(1:end-1,1:end-1) + G(1:end-1,2:end) + G(2:end,1:end-1) + G(2:end,2:end);
result = sum(F(:))/4*dphi*dtheta*
Do you know why F variable is so long?
5 Kommentare
darova
am 12 Apr. 2020
Sorry, big THETA here
F = F .* R^2 .* cos(THETA(2:end,2:end)); % correction of elementary volume
It's late today. Im going to sleep. I'll respond tomorrow
darova
am 13 Apr. 2020
As for volume calculations:

I suggest you to use 3D matrices:
theta = ...
phi = ..
rr = ...
dth = theta(2) - theta(1);
dphi = phi(2) - phi(1);
dr = rr(2) - rr(1);
[T,P,R] = meshgrid(theta,phi,rr); % create 3D matrices
Integral 3
dV = (your long function) .* R.^2 .*cos(T) *dr*dth*dphi;
Now there is need to 'averaging' as before but for 3D matrices
Maybe there is better idea but i have only this:
dV = dV(1:end-1,1:end-1,1:end-1) + ...
dV(1:end-1,1:end-1,2:end) + ...
dV(1:end-1,2:end,1:end-1) + ...
dV(2:end,2:end,1:end-1) + ...
% 4 more combinations
dV = sum(dV(:))/8;
There is one more idea, but nor precise one (without averaging). Just create dense mesh
dV1 = dV(2:end,2:end,2:end);
dV1 = sum(dV1);
Weitere Antworten (0)
Siehe auch
Kategorien
Mehr zu Numerical Integration and Differentiation finden Sie in Help Center und File Exchange
Produkte
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!