Damping and frequency from simulation data
15 Ansichten (letzte 30 Tage)
Ältere Kommentare anzeigen
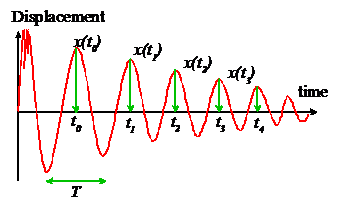
I have some simulation data, for example y in the attachment. I can manually calculate the damping and frequency with logarithmic decrement, but can I do this automated? I can't seem to figure out how.
And/or can I fit a nonlinear function through my datapoints? I tried polyfit but that doesn't work with time series.
2 Kommentare
Ameer Hamza
am 2 Apr. 2020
How do you manually calculate the damping and frequency? Is there a mathematical formula? What type of nonlinear fit do you want to fit your data?
Antworten (1)
Ameer Hamza
am 3 Apr. 2020
The following code automatically estimate the parameters from the signal.
load('PositionY_example.mat');
[val, locs] = findpeaks(y.Data);
peak_times = y.Time(locs);
t0 = t(locs(1));
tn = t(locs(2:end));
omega = mean((1:numel(tn))'./(tn-t0));
xt0 = val(1);
xtn = val(2:end);
delta = mean(log(xtn./xt0)./(1:numel(xtn))');
zeta = delta/sqrt(4*pi^2+delta^2);
As you already know the value of ω, δ, and ζ of your signal, you can calculate the nonlinear fit for your data using this equation.
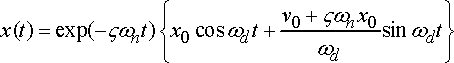
2 Kommentare
MD Riaz Pervez
am 28 Apr. 2023
t represent time. Here use t=Time therefore change that to make a single
Siehe auch
Kategorien
Mehr zu Nonlinear Control finden Sie in Help Center und File Exchange
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!