ilwt2
Description
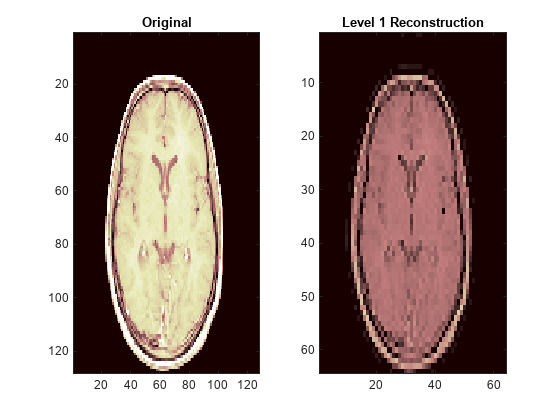
xr = ilwt2(ll,lh,hl,hh)ll, and the horizontal
(lh), vertical (hl), and diagonal
(hh) wavelet coefficients. By default,
ilwt2 assumes that you used the lifting scheme
associated with the db1 wavelet to obtain the coefficients.
If you have not modified the coefficients, xr is a perfect
reconstruction of the signal.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
References
[1] Strang, Gilbert, and Truong Nguyen. Wavelets and Filter Banks. Rev. ed. Wellesley, Mass: Wellesley-Cambridge Press, 1997.
[2] Sweldens, Wim. “The Lifting Scheme: A Construction of Second Generation Wavelets.” SIAM Journal on Mathematical Analysis 29, no. 2 (March 1998): 511–46. https://doi.org/10.1137/S0036141095289051.
Extended Capabilities
Version History
Introduced in R2021bSee Also
lwt2 | lwtcoef2 | haart2 | ihaart2 | liftingScheme