Diese Seite wurde mithilfe maschineller Übersetzung übersetzt. Klicken Sie hier, um das englische Original zu sehen.

Visualisieren Sie die Windgeschwindigkeit als Funktion der Umgebungstemperatur und des Drucks

In diesem Beispiel verwendet:

Script öffnen

Dieses Beispiel zeigt, wie die Variation der Windgeschwindigkeit als Funktion der Umgebungslufttemperatur und des Umgebungsluftdrucks mithilfe von Curve Fitting Toolbox ™ visualisiert werden kann. Sie lesen ThingSpeak™-Daten von einer Wetterstation und verwenden dann ein 3D-Diagramm, um die Daten und die Anpassung zu visualisieren.

Daten vom Kanal der Wetterstation ThingSpeak lesen

ThingSpeak-Kanal 12397 enthält Daten von der Wetterstation MathWorks in Natick, Massachusetts. Die Daten werden einmal pro Minute erfasst. Die Felder 2, 4 und 6 enthalten jeweils Daten zu Windgeschwindigkeit, Temperatur und Luftdruck.

% Read the data using the |thingSpeakRead| function from channel 12397 on a particular week. For example, the week of May 1, 2018.

startDate = datetime('May 1, 2018 0:0:0');
endDate = datetime('May 8, 2018 0:0:0');
data = thingSpeakRead(12397,'daterange',[startDate endDate],'Fields',[2 4 6],'outputFormat','table');

Passen Sie eine Oberfläche an die Daten an

Änderungen des Luftdrucks und der Temperatur wirken sich auf die Windgeschwindigkeit aus. Nehmen wir an, dass die Schwankung der Windgeschwindigkeit durch ein Polynom zweiten Grades der Umgebungstemperatur und des Umgebungsdrucks erklärt wird. Verwenden Sie die Funktion fit, um eine quadratische Oberfläche anzupassen.

fitObject = fit([data.TemperatureF,data.PressureHg],data.WindSpeedmph,'poly22');

Plotten Sie die angepassten Daten

Sie können die angepassten Daten grafisch darstellen, um zu sehen, ob eine quadratische Oberflächenanpassung die Variation der Windgeschwindigkeit erfasst.

plot(fitObject,[data.TemperatureF,data.PressureHg],data.WindSpeedmph);
xlabel('Ambient Temperature [^{\circ}F]');
ylabel('Ambient Air Pressure [inHg]');
zlabel('Wind Speed [mph]');
title('Wind Speed as a Function of Ambient Temperature and Pressure','FontSize',10);

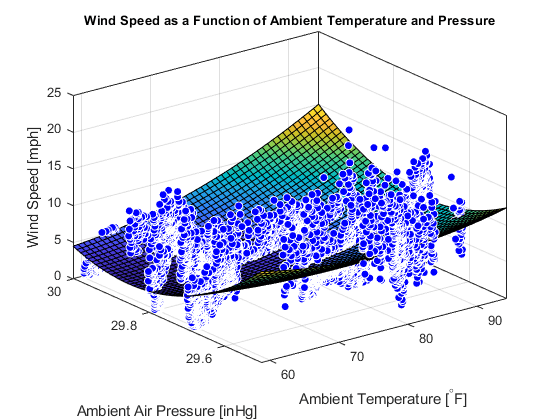
Die quadratische Anpassung scheint einen guten Durchschnitt für die schwankenden Windgeschwindigkeitsdaten zu liefern. An diesem Frühlingstag ist die Windgeschwindigkeit mit steigendem Druck parabolisch, nimmt jedoch bei höheren Temperaturen zu.

Siehe auch

Funktionen