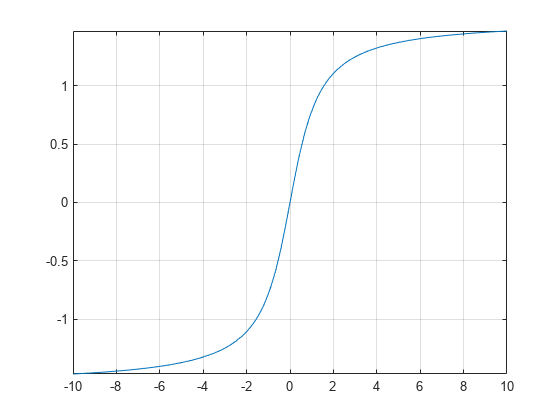
atan
Symbolic inverse tangent
Syntax
Description
P = atan(Z)Z. All angles are
in radians.
For real values of
Z,atan(Z)returns values in the interval[-pi/2,pi/2].For complex values of
Z,atan(Z)returns complex values with the real parts in the interval[-pi/2,pi/2].
P = atan(Y,X)Y and
X. This syntax with two input arguments is the same as atan2(Y,X).
Symbolic arguments X and Y are assumed to be
real, and atan(Y,X) returns values in the interval
[-pi,pi].
Examples
Input Arguments
More About
Version History
Introduced before R2006a