loss
Regression error for regression tree model
Syntax
Description
L = loss(___,Name=Value)
Examples
Compute the In-Sample MSE
Load the carsmall data set. Consider Displacement, Horsepower, and Weight as predictors of the response MPG.
load carsmall
X = [Displacement Horsepower Weight];Grow a regression tree using all observations.
tree = fitrtree(X,MPG);
Estimate the in-sample MSE.
L = loss(tree,X,MPG)
L = 4.8952
Find the Pruning Level Yielding the Optimal In-Sample Loss
Load the carsmall data set. Consider Displacement, Horsepower, and Weight as predictors of the response MPG.
load carsmall
X = [Displacement Horsepower Weight];Grow a regression tree using all observations.
Mdl = fitrtree(X,MPG);
View the regression tree.
view(Mdl,Mode="graph");
Find the best pruning level that yields the optimal in-sample loss.
[L,se,NLeaf,bestLevel] = loss(Mdl,X,MPG,Subtrees="all");
bestLevelbestLevel = 1
The best pruning level is level 1.
Prune the tree to level 1.
pruneMdl = prune(Mdl,Level=bestLevel);
view(pruneMdl,Mode="graph");
Examine the MSE for Each Subtree
Unpruned decision trees tend to overfit. One way to balance model complexity and out-of-sample performance is to prune a tree (or restrict its growth) so that in-sample and out-of-sample performance are satisfactory.
Load the carsmall data set. Consider Displacement, Horsepower, and Weight as predictors of the response MPG.
load carsmall
X = [Displacement Horsepower Weight];
Y = MPG;Partition the data into training (50%) and validation (50%) sets.
n = size(X,1); rng(1) % For reproducibility idxTrn = false(n,1); idxTrn(randsample(n,round(0.5*n))) = true; % Training set logical indices idxVal = idxTrn == false; % Validation set logical indices
Grow a regression tree using the training set.
Mdl = fitrtree(X(idxTrn,:),Y(idxTrn));
View the regression tree.
view(Mdl,Mode="graph");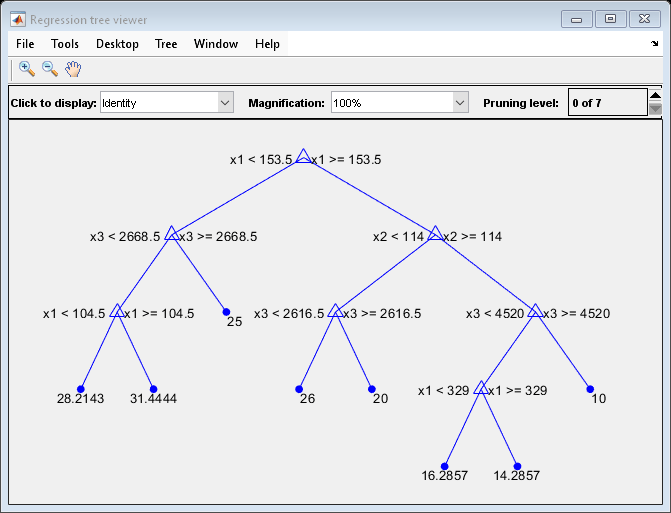
The regression tree has seven pruning levels. Level 0 is the full, unpruned tree (as displayed). Level 7 is just the root node (i.e., no splits).
Examine the training sample MSE for each subtree (or pruning level) excluding the highest level.
m = max(Mdl.PruneList) - 1; trnLoss = resubLoss(Mdl,SubTrees=0:m)
trnLoss = 7×1
5.9789
6.2768
6.8316
7.5209
8.3951
10.7452
14.8445
The MSE for the full, unpruned tree is about 6 units.
The MSE for the tree pruned to level 1 is about 6.3 units.
The MSE for the tree pruned to level 6 (i.e., a stump) is about 14.8 units.
Examine the validation sample MSE at each level excluding the highest level.
valLoss = loss(Mdl,X(idxVal,:),Y(idxVal),Subtrees=0:m)
valLoss = 7×1
32.1205
31.5035
32.0541
30.8183
26.3535
30.0137
38.4695
The MSE for the full, unpruned tree (level 0) is about 32.1 units.
The MSE for the tree pruned to level 4 is about 26.4 units.
The MSE for the tree pruned to level 5 is about 30.0 units.
The MSE for the tree pruned to level 6 (i.e., a stump) is about 38.5 units.
To balance model complexity and out-of-sample performance, consider pruning Mdl to level 4.
pruneMdl = prune(Mdl,Level=4);
view(pruneMdl,Mode="graph")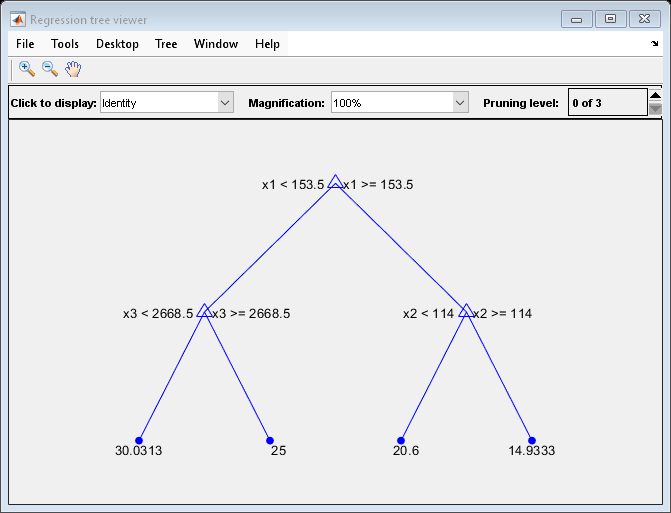
Input Arguments
tree — Regression tree model
RegressionTree model object | CompactRegressionTree model object
Regression tree model, specified as a RegressionTree model object trained with fitrtree, or a CompactRegressionTree model object created with
compact.
Tbl — Sample data
table
Sample data, specified as a table. Each row of Tbl
corresponds to one observation, and each column corresponds to one predictor
variable. Optionally, Tbl can contain additional
columns for the response variable and observation weights.
Tbl must contain all the predictors used to train
tree. Multicolumn variables and cell arrays other
than cell arrays of character vectors are not allowed.
If Tbl contains the response variable used to train
tree, then you do not need to specify
ResponseVarName or Y.
If you trained tree using sample data contained in a
table, then the input data for loss must also be
in a table.
Data Types: table
ResponseVarName — Response variable name
name of a variable in Tbl
Response variable name, specified as the name of a variable in
Tbl. If Tbl contains the
response variable used to train tree, then you do not
need to specify ResponseVarName.
You must specify ResponseVarName as a character
vector or string scalar. For example, if the response variable is stored as
Tbl.Response, then specify it as
"Response". Otherwise, the software treats all
columns of Tbl, including
Tbl.Response, as predictors.
Data Types: char | string
X — Predictor data
numeric matrix
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: L = loss(tree,X,Y,Subtrees="all") specifies to prune
all subtrees.
LossFun — Loss function
"mse" (default) | function handle
Loss function, specified as "mse" (mean squared error) or as a
function handle. If you pass a function handle fun, loss calls it as
fun(Y,Yfit,W)
where Y, Yfit, and W are
numeric vectors of the same length.
Yis the observed response.Yfitis the predicted response.Wis the observation weights.
The returned value of fun(Y,Yfit,W) must be a scalar.
Example: LossFun="mse"
Example: LossFun=@Lossfun
Data Types: char | string | function_handle
subtrees — Pruning level
0 (default) | vector of nonnegative integers | "all"
Pruning level, specified as a vector of nonnegative integers in ascending order or
"all".
If you specify a vector, then all elements must be at least 0 and
at most max(tree.PruneList). 0 indicates the full,
unpruned tree, and max(tree.PruneList) indicates the completely
pruned tree (that is, just the root node).
If you specify "all", then loss
operates on all subtrees, meaning the entire pruning sequence. This specification is
equivalent to using 0:max(tree.PruneList).
loss prunes tree to each level
specified by Subtrees, and then estimates the corresponding output
arguments. The size of Subtrees determines the size of some output
arguments.
For the function to invoke Subtrees, the properties
PruneList and PruneAlpha of
tree must be nonempty. In other words, grow
tree by setting Prune="on" when you use
fitrtree, or by pruning tree using prune.
Example: Subtrees="all"
Data Types: single | double | char | string
TreeSize — Tree size
"se" (default) | "min"
Tree size, specified as one of the following:
"se"— Thelossfunction returnsBestLevelcorresponding to the smallest tree whose MSE is within one standard error of the minimum MSE."min"— Thelossfunction returnsBestLevelcorresponding to the minimal MSE tree.
Example: TreeSize="min"
Data Types: char | string
Weights — Observation weights
ones(size(X,1),1) (default) | name of a variable in Tbl | numeric vector of positive values
Observation weights, specified as a numeric vector of positive values
or the name of a variable in Tbl.
If you specify Weights as a numeric vector, then
the size of Weights must be equal to the number of
rows in X or Tbl.
If you specify Weights as the name of a variable
in Tbl, you must do so as a character vector or
string scalar. For example, if the weights are stored as
Tbl.W, then specify Weights
as "W". Otherwise, the software treats all columns of
Tbl, including Tbl.W, as
predictors.
Example: Weights="W"
Data Types: single | double | char | string
Output Arguments
SE — Standard error of loss
numeric vector
Standard error of loss, returned as a numeric vector that has the same
length as Subtrees.
Nleaf — Number of leaf nodes
numeric vector of nonnegative integers
Number of leaf nodes in the pruned subtrees, returned as a numeric vector
that has the same length as Subtrees. Leaf nodes are
terminal nodes, which give responses, not splits.
BestLevel — Best pruning level
numeric scalar
Best pruning level, returned as a numeric scalar whose value depends on
TreeSize:
When
TreeSizeis"se", thelossfunction returns the highest pruning level whose loss is within one standard deviation of the minimum (L+se, whereLandserelate to the smallest value inSubtrees).When
TreeSizeis"min", thelossfunction returns the element ofSubtreeswith the smallest loss, usually the smallest element ofSubtrees.
More About
Mean Squared Error
The mean squared error m of the predictions f(Xn) with weight vector w is
Extended Capabilities
Tall Arrays
Calculate with arrays that have more rows than fit in memory.
Usage notes and limitations:
Only one output is supported.
You can use models trained on either in-memory or tall data with this function.
For more information, see Tall Arrays.
GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.
Usage notes and limitations:
The
lossfunction does not support decision tree models trained with surrogate splits.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2011a
See Also
MATLAB-Befehl
Sie haben auf einen Link geklickt, der diesem MATLAB-Befehl entspricht:
Führen Sie den Befehl durch Eingabe in das MATLAB-Befehlsfenster aus. Webbrowser unterstützen keine MATLAB-Befehle.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)