Spatial Contact Force
Model spatial contact between two geometries
Libraries:
Simscape /
Multibody /
Forces and Torques
Description
The Spatial Contact Force block models the contact between a pair of geometries in 3-D space. You can use the built-in penalty method or provide custom normal and friction force laws to model a contact.
Supported Geometries
The Spatial Contact Force block can model contacts between a variety of geometry pairs. You can use the geometries exported from the solid blocks in the Body Elements sublibrary or the geometries of the point and surface blocks in the Curves and Surfaces sublibrary.
All the exported geometries are convex hull representations of the corresponding solids even though some of the solids may have concave shapes. The figure shows the true geometry and convex hull representation of an L-shape solid.

Note that when computing inertial properties, the solid blocks use the true geometry.
The Spatial Contact Force block does not model contacts between certain geometry pairs. This table lists the supported pairs.
| Convex Hull of Solid | Disk | Grid Surface | Infinite Plane | Point | Point Cloud | |
| Convex Hull of Solid | Yes | Yes | No | Yes | Yes | Yes |
| Disk | Yes | No | No | Yes | No | No |
| Grid Surface | No | No | No | No | Yes | Yes |
| Infinite Plane | Yes | Yes | No | No | Yes | Yes |
| Point | Yes | No | Yes | Yes | No | No |
| Point Cloud | Yes | No | Yes | Yes | No | No |
Contact Forces
The image shows how the Spatial Contact Force block models a spatial contact problem between two 3-D geometries. In this case, the contact is between a blue base geometry and a red follower geometry and there is one contact point.

During contact, each geometry has a contact frame. The contact frames are always coincident and located at the contact point. The xy-planes of the contact frames define the contact plane. The z-direction of the contact frames is an outward normal vector for the base geometry, but an inward normal vector for the follower geometry. During continuous contact, the contact frames move around the geometry as the contact point moves.
The block applies contact forces to the geometries at the origin of the contact frames in accordance with Newton's Third Law:
The normal force, , which is aligned with the z-axis of the contact frame. This force pushes the geometries apart in order to reduce penetration.
The frictional force, , which lies in the contact plane. This force opposes the relative tangential velocities between the geometries.
To specify a normal contact force, in the Normal Force section, set
the Method parameter to Smooth Spring-Damper
or Provided by Input. If you select Smooth
Spring-Damper, the normal force is:
,
where:
is the normal force applied in equal-and-opposite fashion to each contacting geometry.
is the penetration depth between two contacting geometries.
is the transition region width specified in the block.
is the first time derivative of the penetration depth.
is the normal-force stiffness specified in the block.
is the normal-force damping specified in the block.
is the smoothing function.
The force law is smoothed near the onset of penetration. When d < w, the smoothing function increases continuously and monotonically over the interval [0, w]. The function is 0 when d = 0, the function is 1 when d = w, and the function has zero derivative with respect to d at the endpoints of the interval.
To better detect contacts when the value of the Transition Region Width parameter is small, the Spatial Contact Force block supports optional zero-crossing detection. The zero-crossing events only occur when the separation distance changes from positive or zero to negative and vice versa.
Note
The zero-crossing detection of the Spatial Contact Force block is different than the zero-crossing detection of other Simulink® blocks, such as From File and Integrator, because the force equation of the Spatial Contact Force is continuous. For more information about zero-crossing detection in Simulink blocks, see Zero-Crossing Detection.
To specify a frictional force, in the Frictional Force section, set
the Method parameter to Smooth Stick-Slip,
Provided by Input, or None. If you
select Smooth Stick-Slip, the frictional force is always directly
opposed to the direction of the relative velocity at the contact point and is related to the
normal force through a coefficient of friction that varies depending on the magnitude of the
relative velocity:
,
where:
is the frictional force.
is the normal force.
is the effective coefficient of friction.
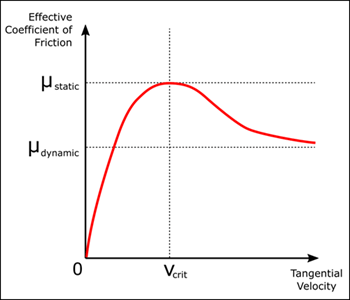
The effective coefficient of friction is a function of the values of the Coefficient of Static Friction, Coefficient of Dynamic Friction, and Critical Velocity parameters, and the magnitude of the relative tangential velocity. At high relative velocities, the value of the effective coefficient of friction is close to that of the coefficient of dynamic friction. At the critical velocity, the effective coefficient of friction achieves a maximum value that is equal to the coefficient of static friction. The graph shows the basic relationship in the typical case where > . In this case, the model is able to approximate stiction with a higher effective coefficient of friction near small tangential velocities.
When modeling contacts that involve a point cloud, the Spatial Contact Force block calculates the contact quantities for each point and the output signals have the same order as the points specified in the Point Could block. For the points that are not in contact with the other geometry, the measured values are zero. When using input forces, the size and order of the input signals must match the size and order of the points specified in the Point Could block.