Discrete-Valued Variables in Response Optimization (Code)
This example shows how to use response optimization to tune discrete-valued variables. Discrete-valued variables represent model parameters that are restricted to a finite set of values, instead of continuously varying. To use discrete-valued variables for response optimization or parameter estimation, you must use the surrogateopt solver for mixed-integer optimization.
Open the Model
In the sdoMotorPosition model, a PI controller enables the angular position of a DC motor to match a desired reference value. The load on the motor is subject to disturbances, and the controller must reject these disturbances.
open_system('sdoMotorPosition')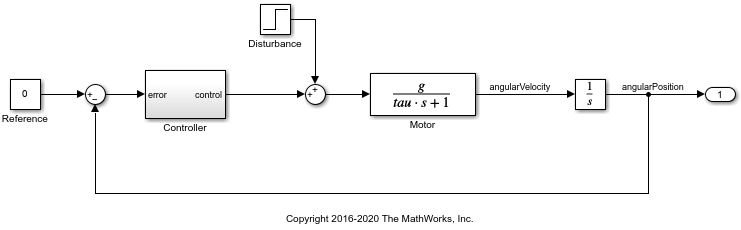
Within the Controller subsystem, the PI gains are set by a 12 V source divided down by resistors R1, R2, R3, and R4, as shown in the following diagram.
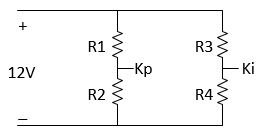
The proportional gain, Kp, is given by 12*R2/(R1+R2) and the integral gain, Ki, is given by 12*R4/(R3+R4). The initial values of the resistances are R1 = 47 kΩ, R2 = 180 kΩ, R3 = 10 kΩ, and R4 = 10 kΩ.
Specify Discrete Design Variables
Those four resistor values are the model parameters to tune for the optimization. Because resistors are only available in discrete values, use discrete parameters to represent them. To do so, use third input argument to sdo.getParameterFromModel to specify discrete parameters.
DesignVars = sdo.getParameterFromModel('sdoMotorPosition',[],{'R1','R2','R3','R4'});
sdo.getParameterFromModel returns an array of param.Discrete parameter objects that correspond to the model parameters in the order you specified. Set the ValueSet property of each parameter to the set of discrete values allowed for the parameter. Set the Value property to the current value, which must be present in ValueSet.
% R1 values DesignVars(1).ValueSet = [39 43 47 51 56] * 1e3; DesignVars(1).Value = 47*1e3; % R2 values DesignVars(2).ValueSet = [150 160 180 200 220] * 1e3; DesignVars(2).Value = 180*1e3; % R3 values DesignVars(3).ValueSet = [8.2 9.1 10 11 12] * 1e3; DesignVars(3).Value = 10*1e3; % R4 values DesignVars(4).ValueSet = [8.2 9.1 10 11 12] * 1e3; DesignVars(4).Value = 10*1e3;
Specify Design Requirements and Signals
The model applies a step disturbance at 1 second. With the initial resistance values specified in the model, the disturbance causes the motor to deviate by about 20°. The response then settles back to within ±5° of the reference position by 4 seconds after the disturbance. For this example, find new resistor values to improve this specification by 10%, so that the motor deviates no more than 18°, and settles back to within ±4.5° degrees of the reference position by 4 seconds after the disturbance. First, specify these new design requirements using sdo.requirements.SignalBound.
Requirements = struct; Requirements.UpperBound = sdo.requirements.SignalBound(... 'BoundMagnitudes', [18 18 ; 4.5 4.5], ... 'BoundTimes', [1 5 ; 5 15]); Requirements.LowerBound = sdo.requirements.SignalBound(... 'BoundMagnitudes', [-4.5 -4.5], ... 'BoundTimes', [5 15], ... 'Type', '>=');
To visualize the initial performance against the requirement, first specify signals to log during simulation. In particular, log the output of the Integrator block, which is the angular position of the model, the signal you want to optimize. To do so, create a simulation scenario with sdo.SimulationTest and configure its LoggingInfo property. Also, to prepare the scenario for later use in the optimization, assign the design variables you created as its Parameters property.
Simulator = sdo.SimulationTest('sdoMotorPosition'); Sig_Info = Simulink.SimulationData.SignalLoggingInfo; Sig_Info.BlockPath = 'sdoMotorPosition/Integrator'; Sig_Info.LoggingInfo.LoggingName = 'Sig'; Sig_Info.LoggingInfo.NameMode = 1; Simulator.LoggingInfo.Signals = Sig_Info; Simulator.Parameters = DesignVars;
Now create a plot of the disturbance-rejection requirements. Then, simulate the model and add the logged signal to the plot.
hRequirement = plot( ... Requirements.LowerBound.BoundTimes', ... Requirements.LowerBound.BoundMagnitudes', ... 'color','black'); hold on plot( ... Requirements.UpperBound.BoundTimes', ... Requirements.UpperBound.BoundMagnitudes', ... 'color','black'); % Simulator.Parameters = DesignVars; Simulator = sim(Simulator); SimLog = find(Simulator.LoggedData, ... get_param('sdoMotorPosition','SignalLoggingName')); Sig_Log = find(SimLog,'Sig'); clrs = colororder; hOriginal = plot(Sig_Log.Values,'Color',clrs(2,:)); legend([hRequirement hOriginal],'Requirement','Original Variables');

The plot shows that the current resistor values do not quite satisfy the more stringent requirement.
Set Up Optimization
The optimization process runs the model many times with different values for the resistor variables. To expedite this, configure the simulator for fast restart.
Simulator = setup(Simulator,FastRestart='on');Optimization requires an objective or cost function that runs the model and determines whether the disturbance rejection requirements are satisfied. For this example, use the function sdoMotorPosition_optFcn, which is included at the end of the example. This function is called many times by the optimization solver. To pass the function to the optimizer, use an anonymous function with one argument that calls sdoMotorPosition_optFcn.
optimfcn = @(P) sdoMotorPosition_optFcn(P,Simulator,Requirements);
Specify optimization options. Set the optimization method to surrogateopt solver, which is the method that supports tuning of discrete parameters.
Options = sdo.OptimizeOptions;
Options.Method = 'surrogateopt';
Options.MethodOptions.MaxFunctionEvaluations = 100;
Options.MethodOptions.ObjectiveLimit = 0.001;
Options.OptimizedModel = Simulator;Optimize the Design
To find resistance values optimized for the requirements, call sdo.optimize with the cost function handle, parameters to optimize, and options.
rng('default'); % for reproducibility [Optimized_DesignVars,Info] = sdo.optimize(optimfcn,DesignVars,Options);
Optimization started 2026-Feb-21, 18:17:43
Current
F-count max constraint max constraint Trial type
1 0.0759805 0.0759805 initial
2 0.0751287 0.0751287 random
3 0.0751287 0.179179 random
4 0.0447169 0.0447169 random
5 0.0317818 0.0317818 random
6 0.0317818 0.261353 random
7 0.0257711 0.0257711 random
9 0.0257711 0.0971938 random
10 0.0257711 0.200359 random
11 0.0062997 0.0062997 random
13 0.0062997 0.0818387 random
14 0.0062997 0.0585416 random
16 0.0062997 0.112485 random
17 0.0062997 0.0759805 random
18 0.0062997 0.0709489 random
20 0.0062997 0.099985 random
21 -0.00759693 -0.00759693 adaptive
22 -0.00759693 0.0691728 random
23 -0.00759693 0.0347164 random
25 -0.00759693 0.0589627 random
26 -0.00759693 0.131778 random
27 -0.00759693 0.147347 random
29 -0.00759693 0.0534262 random
30 -0.00759693 0.1643 random
31 -0.00759693 0.0419731 random
33 -0.00759693 0.077945 random
34 -0.00759693 0.0883493 random
37 -0.00762259 0.13976 random
38 -0.00762259 0.140634 random
41 -0.00762259 0.0348764 random
42 -0.00762259 0.18995 random
44 -0.00762259 0.0597358 random
45 -0.00762259 0.015983 random
46 -0.00762259 0.0770592 random
48 -0.00762259 0.081758 random
49 -0.00762259 0.0240828 random
50 -0.00762259 0.173292 random
52 -0.00762259 0.217099 random
53 -0.00762259 0.104371 random
54 -0.00762259 0.0937562 random
55 -0.00762259 0.104225 random
57 -0.00762259 0.150819 random
58 -0.00762259 0.0636666 random
59 -0.00762259 0.0320499 random
61 -0.00762259 0.0798937 random
62 -0.00762259 0.174146 random
63 -0.00762259 0.0166127 random
65 -0.00762259 0.294106 random
66 -0.00518218 -0.00518218 adaptive
67 -0.00518218 0.0319864 random
69 -0.00518218 0.0342618 random
70 -0.00518218 0.0982987 random
73 -0.00518218 0.299815 random
74 -0.00518218 0.0712971 random
77 -0.00518218 0.131778 random
78 -0.00518218 0.00653156 random
81 -0.00518218 0.0689487 random
82 -0.00518218 0.0257711 random
85 -0.00518218 0.112485 random
86 -0.00518218 0.06706 random
87 -0.00518218 0.0751287 random
88 -0.00737024 -0.00737024 adaptive
89 -0.00737024 0.0759805 random
90 -0.00737024 0.10447 random
91 -0.00737024 0.190644 random
92 -0.00737024 0.142755 random
94 -0.00737024 0.100237 random
95 -0.00737024 0.097787 random
96 -0.00737024 0.0735855 random
98 -0.00737024 0.0783709 random
99 -0.00737024 0.0875674 random
100 -0.00737024 0.0794652 random
Evaluate Optimized Design
Plot the model response after optimization.
Simulator.Parameters = Optimized_DesignVars; Simulator = sim(Simulator); SimLog = find(Simulator.LoggedData, ... get_param('sdoMotorPosition','SignalLoggingName')); Sig_Log = find(SimLog,'Sig'); clrs = colororder; hOptimized = plot(Sig_Log.Values, 'Color', clrs(1,:)); legend([hRequirement hOriginal hOptimized], ... 'Requirement','Original Variables','Optimized Variables');

Now the motor position is within the spec of the disturbance rejection requirement.
Update Model with Optimized Parameter Values
sdo.Optimize returns tuned versions of the parameters in the array Optimized_DesignVars. Each entry in this array is a param.Discrete parameter object whose Value property is set to the optimized value. For instance, examine the new value of R2.
Optimized_DesignVars(2).Value
ans = 220000
Update the model with the optimized parameter values.
sdo.setValueInModel('sdoMotorPosition',Optimized_DesignVars);Restore the simulator fast restart settings.
Simulator = restore(Simulator);
Conclusion
In this example you tuned variables to improve the disturbance rejection characteristics of a motor controller. The variables being tuned were electrical component parts that could only take on discrete values, rather than continuous values. You used sdo.getParameterFromModel to specify the variables as discrete, and used the surrogateopt solver to tune the parameters.
Objective Function
The function sdoMotorPosition_optFcn is called at each iteration of the optimization problem with a set of parameter values, P. The function returns the objective value and constraint violations, Vals, to the optimization solver. See sdo.optimize for a more detailed description of the function signature.
function Vals = sdoMotorPosition_optFcn(P,Simulator,Requirements) %SDOMOTORPOSITION_OPTFCN % % Simulate the model. Simulator.Parameters = P; Simulator = sim(Simulator); % Retrieve logged signal data. SimLog = find(Simulator.LoggedData, ... get_param('sdoMotorPosition','SignalLoggingName')); Sig_Log = find(SimLog,'Sig'); % Evaluate the design requirements. Cleq_UpperBound = evalRequirement( ... Requirements.UpperBound,Sig_Log.Values); Cleq_LowerBound = evalRequirement( ... Requirements.LowerBound,Sig_Log.Values); % Collect the evaluated design requirement values in a structure to % return to the optimization solver. Vals.Cleq = [... Cleq_UpperBound(:); ... Cleq_LowerBound(:)]; end
See Also
sdo.optimize | param.Discrete | sdo.getParameterFromModel | sdo.OptimizeOptions