Main Content

Batch Linearize Model for Parameter Value Variations Using Model Linearizer

This example shows how to use the Model Linearizer to batch linearize a Simulink® model. You vary model parameter values and obtain multiple open-loop and closed-loop transfer functions from the model.

The scdcascade model used for this example contains a pair of cascaded feedback control loops. Each loop includes a PI controller. The plant models, G1 (outer loop) and G2 (inner loop), are LTI models. In this example, you use Model Linearizer to vary the PI controller parameters and analyze the inner-loop and outer-loop dynamics.

Open Model Linearizer for the Model

At the MATLAB® command line, open the Simulink model.

openExample("scdcascade")

To open the Model Linearizer, in the Simulink model window, in the Apps gallery, click Model Linearizer.

Vary the Inner-Loop Controller Gains

To analyze the behavior of the inner loop, very the gains of the inner-loop PI controller, C2. As you can see by inspecting the controller block, the proportional gain is the variable Kp2, and the integral gain is Ki2. Examine the performance of the inner loop for two different values of each of these gains.

In the Parameter Variations drop-down list, click Select parameters to vary.

The Parameter Variations tab opens. click Manage Parameters.

In the Select model variables dialog box, check the parameters to vary, Ki2 and Kp2.

Click OK.

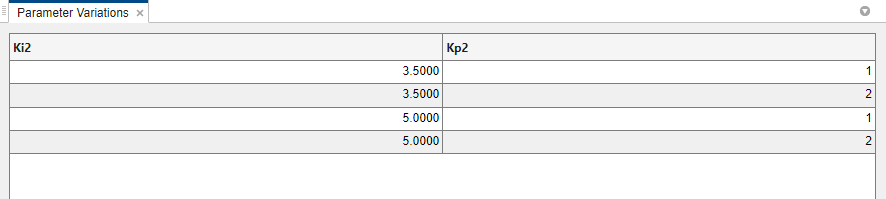
The selected variables appear in the Parameter Variations table. Each column in the table corresponds to one of the selected variables. Each row in the table represents one (Ki2,Kp2) pair at which to linearize the model. These parameter-value combinations are called parameter samples. When you linearize, Model Linearizer computes as many linear models as there are parameter samples, or rows in the table.

Specify the parameter samples at which to linearize the model. For this example, specify four (Ki2,Kp2) pairs, (Ki2,Kp2) = (3.5,1), (3.5,2), (5,1), and (5,2). Enter these values in the table manually. To do so, select a row in the table. Then, select Insert Row > Insert Row Below twice.

Edit the values in the table as shown to specify the four (Ki2,Kp2) pairs.

Tip

For more details about specifying parameter values, see Specify Parameter Samples for Batch Linearization

Analyze the Inner Loop Closed-Loop Response

To analyze the inner-loop performance, extract a transfer function from the inner-loop input u1 to the inner-plant output y2, computed with the outer loop open. To specify this I/O for linearization, in the Linear Analysis tab, in the Analysis I/Os drop-down list, select Create New Linearization I/Os.

Specify the I/O set by creating:

  • An input perturbation point at u1

  • An output measurement point at y2

  • A loop break at e1

Name the I/O set by typing InnerLoop in the Variable name field of the Create linearization I/O set dialog box. The configuration of the dialog box is as shown.

Tip

For more information about specifying linearization I/Os, see Specify Portion of Model to Linearize.

Click OK.

Now that you have specified the parameter variations and the analysis I/O set for the inner loop, linearize the model and examine a step response plot. Click Step.

Model Linearizer linearizes the model at each of the parameter samples you specified in the Parameter Variations table. A new variable, linsys1, appears in the Linear Analysis Workspace section of the Data Browser. This variable is an array of state-space (ss) models, one for each (Ki2,Kp2) pair. The plot shows the step responses of all the entries in linsys1. This plot gives you a sense of the range of step responses of the system in the operating ranges covered by the parameter grid.

Vary the Outer-Loop Controller Gains

Examine the overall performance of the cascaded control system for varying values of the outer-loop controller, C1. To do so, vary the coefficients Ki1 and Kp1, while keeping Ki2 and Kp2 fixed at the values specified in the model.

In the Parameter Variations tab, click Manage Parameters. Clear the Ki2 and Kp2 checkboxes, and check Ki1 and Kp1. Click OK.

Use Model Linearizer to generate parameter values automatically. Click Generate Values. In the Values column of the Starting Values table, enter an expression specifying the possible values for each parameter. For example, vary Kp1 and Ki1 by ± 50% of their nominal values, by entering expressions as shown.

The All Combinations gridding method generates a complete parameter grid of (Kp1,Ki1) pairs, to compute a linearization at all possible combinations of the specified values. To replace all values in the Parameter Variations table with the generated values, elect Overwrite previous values and click OK.

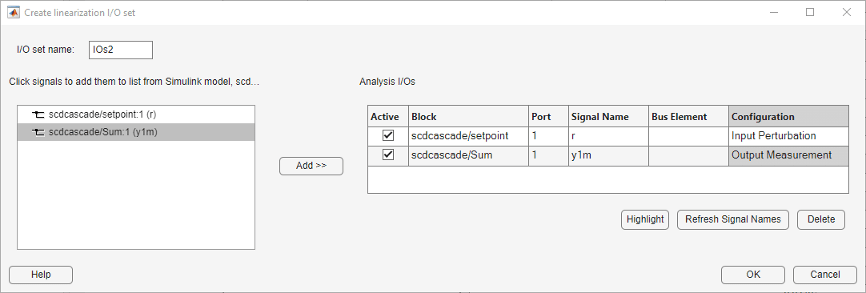
Because you want to examine the overall closed-loop transfer function of the system, create a new linearization I/O set. In the Linear Analysis tab, in the Analysis I/Os drop-down list, select Create New Linearization I/Os. Configure r as an input perturbation point, and the system output y1m as an output measurement. Click OK.

Linearize the model with the parameter variations and examine the step response of the resulting models. Click Step to linearize and generate a new plot for the new model array, linsys2.

The step plot shows the responses of every model in the array. This plot gives you a sense of the range of step responses of the system in the operating ranges covered by the parameter grid.

Note

Although the new plot reflects the new set of parameter variations, Step Plot 1 and linsys1 are unchanged. That plot and array still reflect the linearizations obtained with the inner-loop parameter variations.

Further Analysis of Batch Linearization Results

The results of both batch linearizations, linsys1 and linsys2, are arrays of state-space (ss) models. Use these arrays for further analysis in any of several ways:

Also see Validate Batch Linearization Results for information about validating linearization results in the MATLAB workspace.

Related Topics