Frequency Response Estimation in Model Linearizer Using Pseudorandom Binary Sequence
This example shows how to identify a frequency domain model using a pseudorandom binary sequence (PRBS) for a power electronics system modeled in Simulink® using Simscape™ Electrical™ components. This example addresses the frequency response estimation process in the controller design workflow using a PRBS as the input signal.
Typically, power electronics systems cannot be linearized because they use high-frequency switching components, such as pulse-width modulation (PWM) generators. However, most Simulink Control Design™ PID tuning tools design PID gains based on a linearized plant model. To obtain such a model for a power electronics model that cannot be linearized, you can estimate the plant frequency response over a range of frequencies, as shown in this example.
To collect frequency response data, you can:
Estimate the plant frequency response at the command line.
Estimate the plant frequency response using the Model Linearizer app.
This example shows how to estimate the plant frequency response in Model Linearizer. To learn how to estimate the plant frequency response for a power electronics system at the command line using PRBS input signal, see Frequency Response Estimation for Power Electronics Model Using Pseudorandom Binary Signal.
Boost Converter Model
This example uses a boost converter model as a power electronics system. A boost converter circuit converts one DC voltage to another, typically higher, DC voltage by controlled chopping or switching of the source voltage.
mdl = 'scdboostconverter';
open_system(mdl)
This model uses a MOSFET driven by a PWM signal for switching. The output voltage is regulated to the reference value . A digital PID controller adjusts the PWM duty cycle, , based on the voltage error signal. For this example, you estimate the frequency response from the PWM duty cycle to the load voltage .
Simscape Electrical software contains predefined blocks for many power electronics systems. This model contains a variant subsystem with two versions of the boost converter model:
Boost converter circuit constructed using electrical power components. The parameters of the circuit components are based on [1].
Boost converter block configured to have the same parameters as the boost converter circuit. For more information on this block, see Boost Converter (Simscape Electrical).
To use the Boost Converter block version of the subsystem, in the model, click Boost Converter Block or use the following command.
set_param([bdroot '/Boost Converter'],... 'OverrideUsingVariant','block_boost_converter');
Open Model Linearizer and Find Model Operating Point
To open the Model Linearizer, in the Simulink model window, in the Apps gallery, click Model Linearizer.
To estimate the frequency response for the boost converter, you must first determine the steady-state operating point at which you want the converter to operate. For more information on finding operating points, see Find Steady-State Operating Points for Simscape Models. For this example, use an operating point estimated from a simulation snapshot at 0.045 seconds.
To specify the simulation snapshot time, in the Model Linearizer, on the Linear Analysis tab, in the Operating Point list, select Take Simulation Snapshot.
In the Enter snapshot times to linearize dialog box, in the Simulation snapshot times field, enter 0.045.

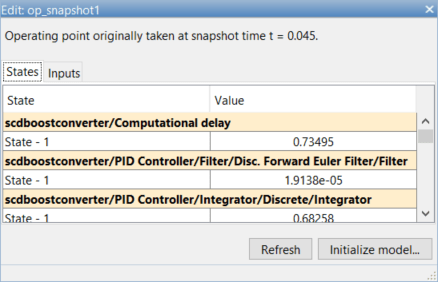
Click Take Snapshots to find the model operating point. An operating point, op_snapshot1, appears in the Data Browser, in the Linear Analysis Workspace section.
To initialize the model with the computed operating point, double-click op_snapshot1, and then in the Edit dialog box click Initialize Model.
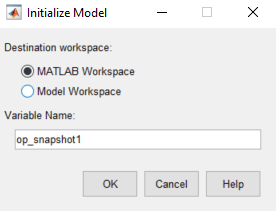
In the Initialize Model dialog box, specify a Variable Name for the operating point object. Alternatively, you can use the default variable name.
To export the operating point to the MATLAB® workspace and set the model initial condition to this operating point, click OK.
Specify Portion of Model to Estimate
By default, Model Linearizer uses the linearization analysis points defined in the model (the model I/Os) to determine where to inject the test signal and where to measure the frequency response. The model scdboostconverter contains predefined linear analysis points: an input point at the PID controller output and an open-loop output before the negative feedback sum block.
If you want to obtain the frequency response of a different portion of the model, on the Estimation tab of Model Linearizer, use the Analysis I/Os drop-down list. Analysis points for estimation work the same way as analysis points for linearization. For more information about linear analysis points, see Specify Portion of Model to Linearize.
Create Pseudorandom Binary Sequence Input Signal
A PRBS is a periodic, deterministic signal with white-noise-like properties that shifts between two values. A PRBS is an inherently periodic signal with a maximum period length of , where is the PRBS order.
To create a PRBS input signal, in the Model Linearizer, on the Estimation tab, under Input Signal, select PRBS Pseudorandom Binary Sequence.
In the Create PRBS input dialog box, first set the Sample time to 5e–6 to match the sample time at the point of input signal injection in the model. Next, specify the frequency range as 300 rad/s to 30000 rad/s using the Min and Max parameters, and then click Compute Parameters. The software computes the signal parameters Number of periods and Signal order based on the specified frequency range. Automatic parameter determination helps create an input signal that leads to an accurate frequency response over a specified frequency range.
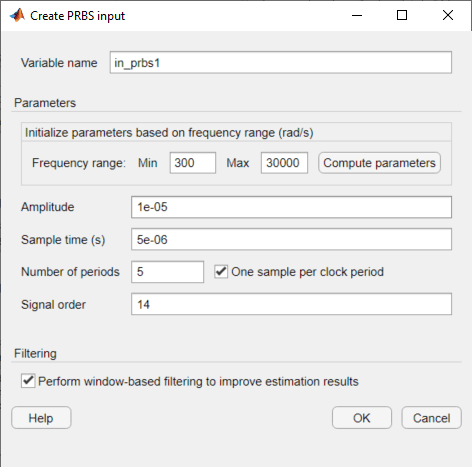
To use a nonperiodic PRBS, set the Number of periods parameter to 1.
To ensure that the system is properly excited, set the perturbation amplitude to 0.05 using the Amplitude parameter. If the input amplitude is too large, the boost converter operates in discontinuous-current mode. If the input amplitude is too small, the PRBS is indistinguishable from ripples in the power electronic circuits.
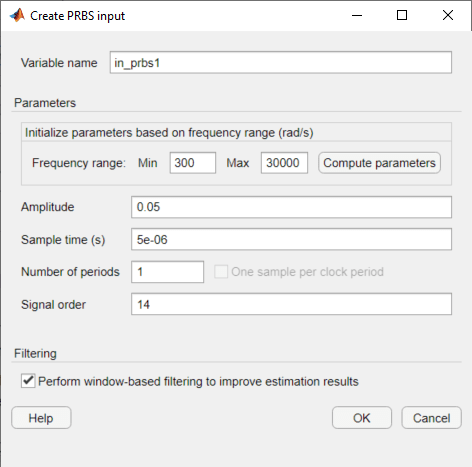
Click OK. The software adds the PRBS signal to the Linear Analysis Workspace.
Collect Frequency Response Data
In the Estimation tab, select op_snapshot1 as the estimation operating point.

Find all source blocks in the signal paths of the linearization outputs that generate time-varying signals. Such time-varying signals can interfere with the signal at the linearization output points and produce inaccurate estimation results. To disable the time-varying source blocks, click More Options. In the Options for frequency response estimation dialog box, on the Time Varying Sources tab, click Find and add time varying source blocks automatically.

Close the dialog box after block paths appear.
To estimate and plot the frequency response, on the Estimation tab, click Bode. The estimated system, estsys1, appears in the Linear Analysis Workspace and is added to Bode Plot 1.
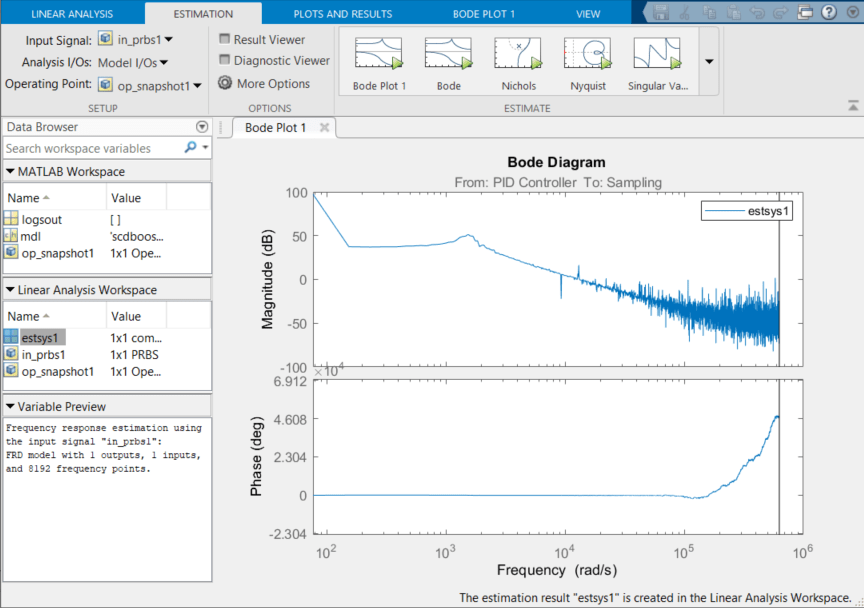
Frequency Response Estimation Result Thinning
Frequency response estimation with PRBS input signal produces results with a large number of frequency points. You can use the Result Thinning functionality to extract an interpolated result from an estimated frequency response model across a specified frequency range and number of frequency points.
To extract the result over the desired frequency range of 300 rad/s to 30000 rad/s, select estsys1 in the Linear Analysis Workspace, and on the Plots and Results tab click Result Thinning. In the Specify frequencies dialog box, enter a frequency range 300 rad/s to 30000 rad/s. Also, specify 30 logarithmically spaced frequency points.
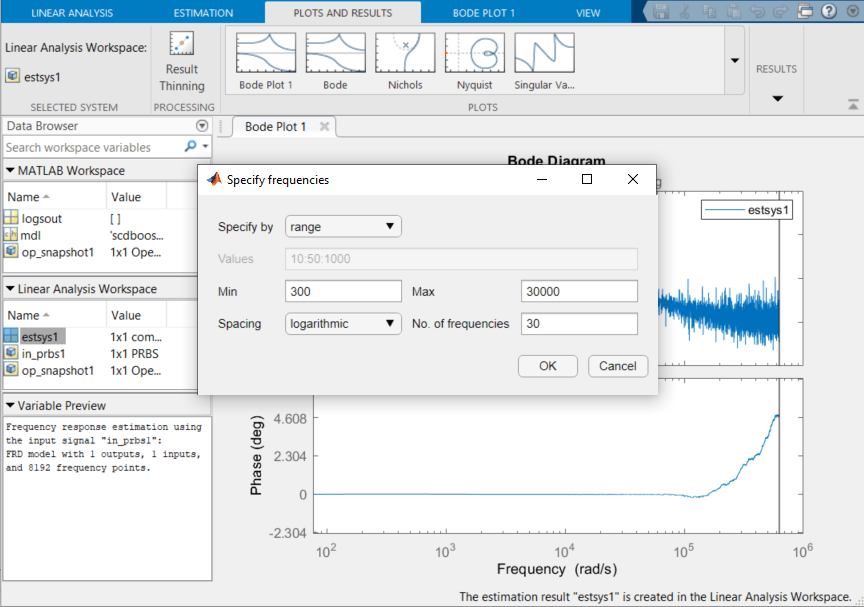
Click OK. The estimated system, estsys1_thinned, appears in the Linear Analysis Workspace. To plot the thinned result, select estsys1_thinned and click Bode.

Compare Frequency Response Data to Sinestream FRE Results
In the Model Linearizer, you can also compare the frequency response data with the result obtained using a sinestream signal. Load the supplied frequency response estimation result using the following command.
load frdSinestreamThe result estsysSinestream is a model with 15 logarithmically spaced frequencies estimated using a sinestream ranging from 50 Hz to 5 kHz.
To compare the sinestream result to the thinned result in the Model Linearizer, select estsysSinestream in the MATLAB Workspace pane of Data Browser and click Bode Plot 2.

To find the final simulation time taken for frequency response estimation by an input signal, select the input signal in the Linear Analysis Workspace and view the simulation time in the Variable Preview pane of the Model Linearizer. Alternatively, you can export the input signals to MATLAB Workspace and use the getSimulationTime function. Load a previously saved session for this example.
load boostconv_frdPRBS.mat
tfinal_sinestream = in_sine1.getSimulationTimetfinal_sinestream = 0.2833
tfinal_prbs = in_prbs1.getSimulationTime
tfinal_prbs = 0.0819
The simulation time with in_prbs1 is about 30% of the time taken by in_sine1 to estimate the frequency response of the model. This indicates that the frequency response estimation with PRBS input signal is much faster than the sinestream input signal.
The estimated frequency response result estsys1_thinned closely matches estsysSinestream. Because the PRBS input signal estimates frequency responses with a large number of frequency points, the estimation result provides more information about the resonant characteristics of the system. To get similar results using a sinestream input signal, you might need to increase the number of frequency points, which results in an increase in estimation time. You can use this approach to obtain accurate frequency response estimation results in a shorter simulation time as compared to estimation with sinestream signals.
Close the model.
close_system(mdl,0)
References
[1] Lee, S. W. Practical Feedback Loop Analysis for Voltage-Mode Boost Converter. Application Report SLVA633. Texas Instruments, 2014. https://www.ti.com/lit/an/slva633/slva633.pdf.