Multiple Design Points in slTuner Interface
For tuning a gain-scheduled control system, you must make your Simulink® model linearize to an array of LTI models corresponding to the various operating
conditions that are your design points. Thus, after you obtain a family of linear plant models
as described in Plant Models for Gain-Scheduled Controller Tuning, you must associate
it with the slTuner interface to your Simulink model. To do so, you use block substitution to cause
slTuner replace the plant subsystem of the model with the array of
linear models. This process builds a family of tunable closed-loop models within the
slTuner interface.
Block Substitution for Plant
Suppose that you have an array of linear plant models obtained at each operating point in your design grid. In the most straightforward case, the following conditions are met:
The linear models in the array correspond exactly to the plant subsystem in your model.
Other than the elements you want to tune, nothing else in the model varies with the scheduling variables.
For a Simulink model mdl containing plant subsystem G,
and a linear model array Garr that represents the plant at a grid of
design points, the following commands create an slTuner
interface:
BlockSubs = struct('Name','mdl/G','Value',Garr); st0 = slTuner('mdl',{'Kp','Ki'},BlockSubs);
st0 contains a family of closed-loop linear models, each linearized
at a design point, and each with the corresponding linear plant inserted for
G. If 'Kp'and 'Ki' are the gain
schedules you want to tune (such as lookup tables), you can parameterize them with tunable
gain surfaces, as described in Parameterize Gain Schedules, and tune them.
Multiple Block Substitutions
In other cases, the linearized array of plant models you have might not correspond exactly to the plant subsystem in your Simulink model. Or, you might need to replace other parts of the model that vary with operating condition. In such cases, more care is needed in constructing the correct block substitution. The following sections highlight several such cases.
For instance, consider the model of the following illustration.

This model has an inner loop with a proportional-only gain-scheduled controller. The
controller is represented by the lookup table Kp_in and the product block
prod. The outer loop includes a PI controller with gain-scheduled
proportional and integral coefficients represented by the lookup tables
Kp and Ki. All the gain schedules depend on the same
scheduling variable alpha.
Suppose you want to tune the inner-loop gain schedule Kp_in with the
outer loop open. To that end, you obtain an array of linear models G_in
from input u to outputs {q,alpha}. This model array
has the wrong I/O dimensions to use as a block substitution for G.
Therefore, you must "pad" G_in with an extra output dimension.
Garr = [0; G_in]; BlockSubs1 = struct('Name','mdl/G','Value',Garr);
In addition, you can remove all effect of the outer loop by replacing the Varying PID Controller block with a system that linearizes to zero at all operating conditions. Because this block has three inputs, replace it with a 3-input, one-output zero system.
BlockSubs2 = struct('Name','mdl/Varying PID Controller','Value',ss([0 0 0]));
With those block substitutions, the following commands create an
slTuner interface that you might use to tune the inner-loop gain
schedule.
st0 = slTuner('mdl','Kp_in'); st0.BlockSubstitutions = [BlockSubs1; BlockSubs2];
See the example Angular Rate Control in the HL-20 Autopilot for another case in which several elements other than the plant itself are replaced by block substitution.
Substituting Blocks That Depend on the Scheduling Variables
Next, suppose that you have already tuned the inner-loop gain schedule, and have
obtained an array Kp_in_tuned, of values of Kp_in that
correspond to each design point (each value of alpha at which you
linearized the plant). Suppose also that you have a new Garr that is the
full plant from u to {y,q,alpha} linearized with the
tuned inner loop closed. To tune the outer-loop gain schedules, you must replace the product
block with the array Kp_in_tuned. It is important to note that you
replace the injection point, the product block prod, rather than the
lookup table Kp_in. Replacing the product block effectively converts it
to a varying gain. Also, you must zero out the first input of the product block to remove
the effect of the lookup table
Kp_in.
prodsub = [0 ss(Kp_in_tuned)]; BlockSubs1 = struct('Name','mdl/prod','Value',prodsub); BlockSubs2 = struct('Name','mdl/G','Value',Garr); st0 = slTuner('mdl',{'Kp','Ki'}); st0.BlockSubstitutions = [BlockSubs1; BlockSubs2];
The following illustration of a portion of a model highlights another scenario in which
you might need to replace blocks that vary with the scheduling variable. Suppose the
scheduling variable is alpha, and somewhere in your model, an signal
u gets divided by alpha.

To ensure that slTuner linearizes this block correctly at all values
of alpha in the design grid, you must replace it by an array of linear
models, one for each alpha value. This block is equivalent to sending
u through a gain of 1/alpha:
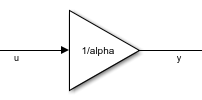
Therefore, you can use the following block substitution in your
slTuner interface, where alphagrid is an array of
alpha values at your design points.
divsub = ss[(1/alphagrid), 0] BlockSubs = struct('Name','mdl/div-by-alpha','Value',divsub); st0.BlockSubstitutions = [st0.BlockSubstitutions; BlockSubs]
Each entry in model array divsub divides its first input by the
corresponding entry in alphagrid, and zeros out its second input. Thus,
this substitution gives the desired result y = u/alpha.
Resolving Mismatches Between a Block and Its Substitution
Sometimes, the linear model array you have is not an exact replacement for the part of the model you want to replace. For example, consider the following illustration of a three-input, one-output subsystem.
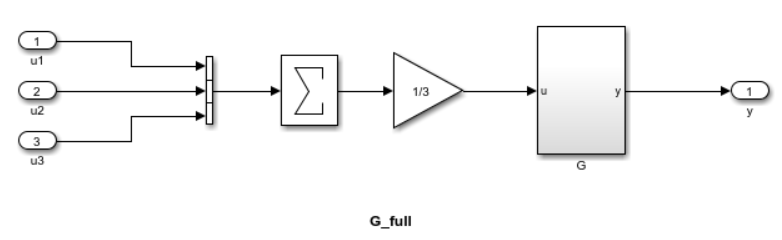
Suppose you have an array of linearized models Garr corresponding to
G. You can configure a block substitution for the entire subsystem
G_full by constructing a substitution model that reproduces the effect
of averaging the three inputs, as follows:
Gsub = Garr*[1/3 1/3 1/3]; BlockSubs = struct('Name','mdl/G_full','Value',Gsub);
Sometimes, you can resolve a mismatch in I/O dimensions by padding inputs or outputs
with zeros, as shown in Multiple Block Substitutions. In still other cases, you might
need to perform other model arithmetic, using commands like series,
feedback, or connect to build a suitable
replacement.
Block Substitution for LPV Blocks
If the plant in your Simulink model is represented by an LPV System , you must still perform
block substitution when creating the slTuner interface for tuning gain
schedules. slTuner cannot read the linear model array directly from the
LPV System block. However, you can use the linear model array specified in
the block for the block substitution, if it corresponds to the design points for which you
are tuning. For instance, suppose your plant is an LPV System block,
LPVPlant, that specifies a model array PlantArray.
You can configure a block substitution for LPVPlant as follows:
BlockSubs = struct('Name','mdl/LPVPlant','Value',PlantArray);