Interpreting Angle in the Angle-Based Rotational Domain

Open Live Script

The angle-based rotational domain tracks angle, theta, and rotational velocity, w, at every node. Use angle-based rotational blocks to model a rotational system where it is important to know many component angles.

This example describes concepts for setting up and interpreting angles in an angle-based rotational network. The example summarizes how to map the Simscape™ schematic axis direction, angles and angular velocity to the physical view of your system in the real world. The example also describes the recommended use of Rotational Spacer (AB) blocks and Rotational Motion Sensor (AB) blocks with angle wrap.

After going through this example, you will understand how to apply the concepts to complete rotational networks, including this clutch plate with springs.

open_system('InterpretingAngleClutchWithSprings');

Views in the Rotational Network

Concept 1: The Rotational Network Shows a Side View and a Front View of an Axis

All blocks in the angle-based rotational domain show a side view of the component on an axis. Block connections are shown in the side view of the axis. Several blocks also include a front view as part of an isometric view. You can configure the front view of isometric blocks to make the Simscape schematic map intuitively to the physical view of your system. In many systems, you may leave the front view at its default setting.

In this image, the Rotational World (AB) and Rotational Spring (AB) show side views of components on the axis. The Rotational Damper (AB) and Inertia (AB) show isometric views that contain both side views and front views.

Placing Parts Along an Axis

Concept 2: You Place Parts on an Axis

In a rotational network, you place parts along a stationary axis to represent your physical system. During a simulation, parts rotate around the axis. The simulation tracks the angle, theta, and angular velocity, w, at every node in the network. Nodes in the Simscape schematic correspond to a location on the axis. Block ports that are connected to the same node are rigidly attached to each other.

The domain models connectivity in the axial direction. Rotational dynamics transmit along the axis even though the domain does not directly model axial length.

Some blocks, such as Inertia (AB), Wheel and Axle (AB-PB), and Cam and Follower (AB-PB) have two rotational ports that are rigidly connected together and have the same value of angle, theta. Displaying two ports for these blocks helps visually align blocks in series on the axis. Other blocks, such as Rotational Spring (AB) and Rotational Damper (AB) have two rotational ports that move relative to each other during simulation. These blocks have a variable Angular length that equals the angle at port F minus the angle at port B.

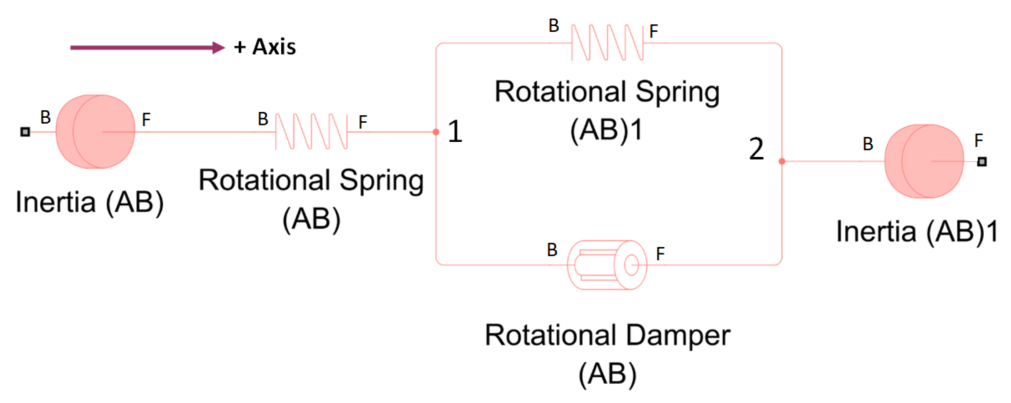
As usual in Simscape, you place parts in parallel to each other if they act in between the same nodes. In this schematic, the Rotational Spring (AB)1 and Rotational Damper (AB) act in between the nodes labeled 1 and 2.

Concept 3: The Rotational World (AB) Block Sets the Stationary Reference Frame

The Rotational World (AB) sets absolute zero angle and angular velocity in the network. That is, the variables theta and w both equal 0 at the node of the Rotational World (AB). The angles of all other nodes are relative to the Rotational World (AB) block. A rotational network may have multiple Rotational World (AB) blocks to represent multiple stationary points with an angle of zero. Add a Rotational Spacer (AB) block to a Rotational World (AB) block to specify a stationary point with a nonzero angle.

Concept 4: Keep Parts Aligned with the Axis Positive Direction

The Simulink® canvas shows block connectivity, not component orientation. Think about the Simulink canvas as a schematic view. You can rotate blocks on the canvas for convenient diagram visualization, however you should keep the positive direction of all blocks aligned with each other for intuitive interpretation of simulated torques. The Interpreting Torque in the Angle-Based Rotational Domain example provides more information on interpreting torques.

Each axis has a positive direction. You set the axis to point left, right, up, or down on the canvas. Two-port blocks have an internal positive direction that points from port B to port F. Once you add the first two-port block to the network and orient it, you designate the axis positive direction. Keep the internal positive direction of all blocks with two ports aligned with the network's positive direction for intuitive interpretation of simulated torques.

In this image, all of the blocks with two ports are aligned so that port B is on the left and port F is on the right. Therefore the axis positive direction points to the right.

Configuring the Positive Rotation Direction

Concept 5: The Rotational Network Obeys a Right-Hand Rule

Rotational motion follows a right-hand rule around the axis. That is, if your right thumb points in the network positive direction, then your curled right fingers indicate the direction of positive rotation around the axis.

This image shows how the right-hand rule relates the positive rotational velocity ( $ω > 0$ ) for three different axes that point to the right, upwards, and downwards.

This concept is an approach for thinking about the physical view and relating the simulated angles, theta, and rotational velocity, w, to your physical view. This concept is convenient for complex rotational systems and necessary for rotational systems that interface with position-based translational networks, as described in the Interfacing Angle-Based Rotational and Position-Based Translational Networks example.

Concept 6: You Configure Block Isometric Views to Indicate the Positive Rotation Direction

All blocks in the angle-based rotational domain show a side view of the component on the axis. The side view is parallel to the axis. The line on the canvas that connects blocks represents a side view of the axis. Many block icons show an isometric view that includes both an axis side view and a front view. The front view is in the plane of rotation.

You configure the isometric view so that the front view represents either the B port or F port. If the front view represents the F port, then the positive axis direction points out of the canvas, and positive rotation is counter-clockwise in the front view, according to the right-hand rule. If the front view represents the B port, then the positive axis direction points into the canvas, and positive rotation is clockwise in the front view.

In this image, the network on the left shows that the front view is associated with port F in the Rotational Damper (AB) and Inertia (AB) blocks. Therefore, the axis points out of the canvas and positive rotation acts counterclockwise in the front view. The network on the right shows that the front view is associated with port B of the Rotational Damper (AB) and Inertia (AB) blocks. Therefore, the axis points into the canvas and positive rotation acts clockwise in the front view.

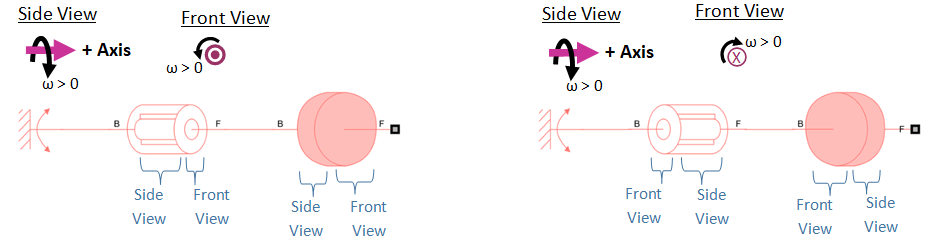
For intuitive diagrams, configure all isometric views in a rotational network so that the front view corresponds to the same port (B or F). Configuring the isometric view makes the Simscape schematic map more intuitively to your physical view for many systems. By default, all isometric views of the components show the front view as port F, so positive values of theta and w are counterclockwise motions. For many rotational systems, this default configuration is sufficient. For some systems, the Simscape schematic maps more intuitively to the physical view if you change the front view to correspond to port B, so that positive values of theta and w are clockwise motions.

The front view configuration affects the functional behavior of the Wheel and Axle (AB-PB) block. For all other blocks it is a visual setting that does not affect the simulated behavior. The Interfacing Angle-Based Rotational and Position-Based Translational Networks example provides more information on the isometric view and Wheel and Axle (AB-PB) block.

Setting the theta = 0 Direction

Concept 7: Define a Direction for theta = 0

In addition to defining the positive axis direction, you define a stationary direction for $θ = 0$ in your physical view. The $θ = 0$ direction is a vector perpendicular to the axis.

In this image, the $θ = 0$ direction points 60 degrees counterclockwise from the vertical in the plane of the front view.

The variable theta that Simscape logs for every node equals 0 when nodes align with the $θ = 0$ direction.

This concept is an approach for thinking about the physical view, not a setting that you directly update on Simscape schematic. Your choice of the $θ = 0$ direction affects how you define initial conditions in the Simscape schematic.

Concept 8: Choose a Reference Point at Each Axial Node

In the physical view of your system, choose a reference vector, or equivalently, a point at a non-zero radius, for each rigid component. This vector (or point) rotates with the component. The Simscape variable theta equals 0 when the reference vector (or point) aligns with the network's $θ = 0$ direction.

In this image, the $θ = 0$ direction points 60 degrees counterclockwise from the vertical in the plane of the front view. The left inertia has an angle of $θ = 60$ degrees. The right inertia has an angle of $θ = 0$ degrees because the reference point aligns with the $θ = 0$ direction.

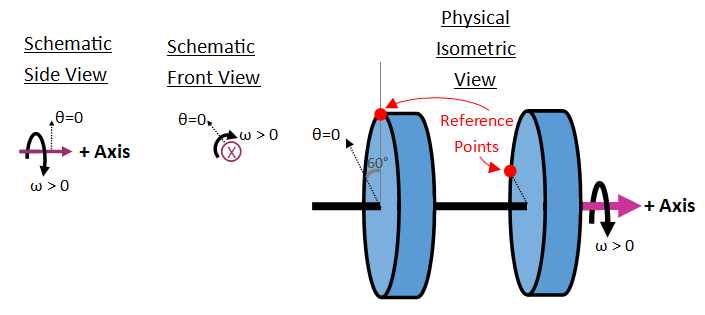
This concept is also an approach for thinking about the physical view, not a setting that you directly update on Simscape schematic. Your choice of the the $θ = 0$ direction affects the theta initial condition settings that you use in your model and how you relate the theta behavior to your physical view.

Basic Example

This example illustrates concepts 1-8 for configuring angles in a rotational network. The system models a rotating inertia with damping. At the start of the simulation, the inertia has an angle of 30 degrees counterclockwise from the vertical and a rotational velocity of 10 deg/s counterclockwise. After 5 seconds, the inertia comes to a rest. This example considers two physical views, and the corresponding Simscape schematics, with different positive rotation directions.

Open the model.

open_system('InterpretingAngleBasic');

In the schematic, a Rotational Initial Spacer (AB) block specifies the initial angle of the inertia block relative to the Rotational World (AB). A Rotational Damper (AB) block acts between the inertia and world block. A Rotational Motion Sensor (AB) block senses the inertia's angle.

In both networks, the positive axis side view points from left to right. In System 1, the front view represents the F port, so the positive axis direction points out of the canvas and positive rotation is in the counterclockwise direction. In System 2, the front view represents the B port, so the positive axis direction points into the canvas and positive rotation is in the clockwise direction. In both networks the $θ = 0$ direction points upwards.

Simulate the system and view the inertia angles (deg) versus time.

open_system('InterpretingAngleBasic/Inertia Angle (deg)');
sim('InterpretingAngleBasic');

Due to the opposing front views in the schematics, the inertia of System 1 initializes at an angle of 30 degrees and rotates with a positive rotational velocity while the inertia of System 2 initializes at -30 degrees and rotates with a negative rotational velocity.

Close the model.

close_system('InterpretingAngleBasic');

Configuring Angle Offsets

Concept 9: Use Rotational Spacer (AB) blocks to offset the angles of different elements

Use a Rotational Spacer (AB) block to add constant angular distance between two points that are rigidly connected. The B and F ports of a Rotational Spacer (AB) block have the same angular velocity, w, but their angles, theta, are offset by the constant Angular length parameter. That is, the angular length is theta_rel = F.theta - B.theta is constant throughout a simulation. The Rotational Spacer (AB) block does not account for any angle-wrap effects.

Clutch with Spring Example

This example illustrates using a Spacer (AB) block to offset angles between elements. This model consists of a large inertia and two friction plates. The first friction plate (blue) connects to the orange plate via a spring, and the orange plate is rigidly connected to the shaft. The right friction plate (yellow) is grounded and serves as a brake plate.

Open the model.

open_system('InterpretingAngleClutchWithEquivalentSpring');

The physical view shows the initial state of the system. The large inertia reference point is initially at an angle of 20 degrees. The reference points of the other plates are all initially at angles of 0 degrees. A Rotational Initial Spacer (AB) block specifies the initial 20-degree angle of the large inertia. A Rotational Spacer (AB) block is in-between the large inertia and orange plate. The rotational spacer has a high-priority angular length of -20 degrees to initialize the orange plate to an angle of 0 degrees. The Rotational Spring (AB) in-between the Orange Plate and Blue Plate has an initial angular length of 0 degrees, so the Blue plate also initializes at 0 degrees. The Brake plate is attached to a World Block, which has an angle of 0 degrees, so the brake plate always has an angle of 0 degrees.

Simulate the model.

open_system('InterpretingAngleClutchWithEquivalentSpring/Angles (deg)');
sim('InterpretingAngleClutchWithEquivalentSpring');

The flywheel initially has an angular velocity of 10 rpm. After 1 second, the brake engages and the large inertia decelerates.

Close the model.

close_system('InterpretingAngleClutchWithEquivalentSpring');

Clutch with Multiple Springs Example

This model is a higher-fidelity version of the Clutch with Spring Example that illustrates using multiple Spacer (AB) blocks to offset angles between elements. Rather than one equivalent spring, the first friction plate (blue) connects to the orange plate via four rotational springs that are in parallel to each other.

Open the model.

open_system('InterpretingAngleClutchWithSprings');

The physical view corresponds to the initial state of the system. The initial states of the four springs are:

Spring	Angular length (deg)	Angle of port B (deg)	Angle of port F (deg)
Top	30	-15	15
Left	60	-120	-60
Right	60	60	120
Bottom	30	-195	-165

To fully specify the system, the model has these high-priority targets:

Large inertia (green) and first friction plate (blue) rotational velocity of 10 rpm.
Torque of 0 Nm for all four springs.
Angular length of all four springs.
Angular length of TopSpring and both top spacers, SpacerTopB and SpacerTopF. These high priority variables fully specify the angle between the orange plate and blue plate as 0 degrees.
Angular length of SpacerLeftB and LeftSpring. Since the left spring branch is in parallel with the top spring branch, which already specifies the angle between the orange and blue plate, the angular length of SpacerLeftF is left as none priority to avoid overconstraining the angles. The solver solves for the angular length of SpacerLeftF equal to 60 degrees that is consistent with making the angle between the orange and blue plates equal to 0 degrees.
Angular length of SpacerRightB, RightSpring, SpacerBotB, and BottomSpring.

Simulate the model.

open_system('InterpretingAngleClutchWithSprings/Angles (deg)');
sim('InterpretingAngleClutchWithSprings');

Equivalently to the Clutch with Spring Example, the large inertia initializes with an angle of 20 degrees while the orange and blue plates initialize at angles of 0 degrees. After 1 second, the brake engages and the large inertia decelerates.

Close the model.

close_system('InterpretingAngleClutchWithSprings');

Configuring Angle Wrap

Concept 10: The Only Block that Models Angle Wrap is the Rotational Motion Sensor (AB)

The Rotational Motion Sensor (AB) can optionally wrap the measured angle to span an interval [X, 2π+X). You set the wrap point, X. Angle wrapping in the sensor makes the simulated angle behavior easier to visualize for some systems.

Pendulum Example

This example illustrates using angle wrap in a Rotational Motion Sensor (AB) block. The pendulum initially has a large rotational velocity so that it revolves around the axis several times before slowing down due to damping.

Open the model.

open_system('InterpretingAnglePendulum');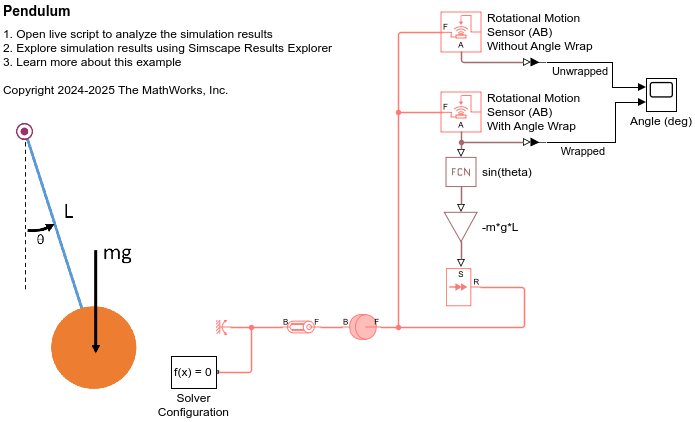

Simulate the model and compare the angles sensed by rotational motion sensors that measured the unwrapped and wrapped angle

open_system('InterpretingAnglePendulum/Angle (deg)');
sim('InterpretingAnglePendulum');

At the beginning of the simulation, the pendulum has a high velocity and completes several revolutions around the pivot point. The Rotational Motion Sensor (AB) block with angle wrap measures the angle over [-180, 180) degrees. Near the end of the simulation, the damper has slowed down the pendulum so that it undergoes smaller oscillations about 0 degrees. Choosing a wrap point of -180 degrees, that is far from the pendulum equilibrium angle, allows the sensor to measure the small oscillations cleanly without any angle-wrap jumps.

Close the model.

close_system('InterpretingAnglePendulum');

Summary

The rotational network schematic shows a side view and a front view of an axis.
In a rotational network, you place parts on an axis.
The Rotational World (AB) block sets the reference frame.
The Simulink canvas shows block connectivity, not component orientation. Parts are always aligned with the positive direction.
Positive rotational motion follows a right-hand rule around the axis.
Configure the view of isometric icons so that all front faces represents either the B port or F port to intuitively match your physical view.
Choose a reference direction for $θ = 0$ .
Choose a reference point on each node. The node logs theta = 0 when the reference point aligns with the $θ = 0$ reference direction.
Use Rotational Spacer (AB) blocks to rigidly offset the angles of different components.
You can wrap the measured angle of the Rotational Motion Sensor (AB) block to clearly visualize motion that spans a large angle range.