Transmission Line (Equivalent Baseband)
Model general transmission line
Libraries:
RF Blockset /
Equivalent Baseband /
Transmission Lines
Description
The Transmission Line block models the transmission line described in the block dialog box in terms of its physical parameters. The transmission line, which can be lossy or lossless, is treated as a two-port linear network. The block enables you to model the transmission line as a stub or as a stubless line.
Parameters
Main
Characteristic impedance of the transmission line, specified as a scalar or complex scalar in ohms.
Propagation velocity of a uniform plane wave on the transmission line, specified as a scalar in meters per seconds.
Reduction in strength of the signal as it travels over the transmission line, specified as a positive scalar in dB/m..
Modeling frequencies, specified as a positive vector in Hz.
Method to interpolate the network parameters, specified as one of the following:
| Method | Description |
|---|---|
Linear | Linear interpolation |
Spline | Cubic spline interpolation |
Cubic | Piecewise cubic Hermite interpolation |
Physical length of the transmission line, specified as a positive scalar in meters.
The block enables you to model the transmission line as a stub or as a stubless line.
Stubless Transmission Line
Not a stub—Not a stubIf you model a coaxial transmission line as stubless line, the Coaxial Transmission Line block first calculates the ABCD-parameters at each frequency contained in the modeling frequencies vector. It then uses the
abcd2sfunction to convert the ABCD-parameters to S-parameters. For more information, see Stub Mode - Not a Stub.The block calculates the ABCD-parameters using the physical length of the transmission line, d, and the complex propagation constant, k, using the following equations:
Z0 is the specified characteristic impedance. k is a vector whose elements correspond to the elements of the input vector
freq. The block calculates k from the specified parameters as k = αa + iβ, where αa is the attenuation coefficient and β is the wave number. The attenuation coefficient αa is related to the specified loss, α, byThe wave number β is related to the specified phase velocity, Vp, by
The phase velocity VP is also known as the wave propagation velocity.
Shunt Transmission Line
Shunt—This parameter provides a two-port network that consists of a stub transmission line that you can terminate with either a short circuit or an open circuit as shown in these diagrams.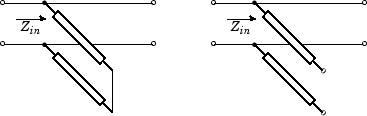
Zin is the input impedance of the shunt circuit and it is calculated as follows:
for a short circuited transmission line
and for the open circuited transmission line
where
Z0 is the characteristic impedance and
is the propagation constant
The ABCD-parameters for the shunt stub are calculated as
Series Transmission Line
Series—This mode parameter provides a two-port network that consists of a series transmission line that you can terminate with either a short circuit or an open circuit as show in these diagrams.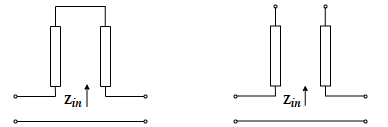
Zin is the input impedance of the series circuit. The ABCD-parameters for the series stub are calculated as
Stub termination for stub modes
Shunt and
Series. Choices are
Open or
Short
Dependencies
To enable this parameter, select
Shunt or
Series in
Stub mode
Visualization
Frequency data source, specified as
User-specified.
Frequency data range, specified as a vector in hertz.
Reference impedance, specified as a nonnegative scalar in ohms.
Type of data plot to visualize using the given data, specified as one of the following:
X-Y plane— Generate a Cartesian plot of the data versus frequency. To create linear, semilog, or log-log plots, set the Y-axis scale and X-axis scale accordingly.Composite data— Plot the composite data. For more information, see Create Plots Using Equivalent Baseband Library Blocks.Polar plane— Generate a polar plot of the data. The block plots only the range of data corresponding to the specified frequencies.Z smith chart,Y smith chart, andZY smith chart— Generate a Smith® chart. The block plots only the range of data corresponding to the specified frequencies.
Type of parameters to plot, specified as one of the following.
S11 | S12 | S21 | S22 |
GroupDelay | GammaIn | GammaOut | VSWRIn |
VSWROut | OIP3 | IIP3 | NF |
NFactor | NTemp | TF1 | TF2 |
TF3 | Gt | Ga | Gp |
Gmag | Gmsg | GammaMS | GammaML |
K | Delta | Mu | MuPrime |
Note
Y parameter1 is disabled when you select Plot type to Composite data.
Type of parameters to plot, specified as one of the following.
S11 | S12 | S21 | S22 |
GroupDelay | GammaIn | GammaOut | VSWRIn |
VSWROut | OIP3 | IIP3 | NF |
NFactor | NTemp | TF1 | TF2 |
TF3 | Gt | Ga | Gp |
Gmag | Gmsg | GammaMS | GammaML |
K | Delta | Mu | MuPrime |
Note
Y parameter2 is disabled when you select Plot type to Composite data.
Plot format, specified as one of the following.
| Y parameter1 | Y format1 |
|---|---|
S11, S12, S21, S22, GammaIn, GammaOut, TF1, TF2, TF3, GammaMS, GammaML, and Delta. | dB, Magnitude (decibels), Abs, Mag, Magnitude (linear), Angle, Angle(degrees), Angle(radians), Real, Imag, and Imaginary. |
GroupDelay | ns, us, ms, s, and ps. |
VSWRIn and VSWROut. | Magnitude (decibels) and None. |
OIP3 and IIP3. | dBm, W, and mW. |
NF | dB and Magnitude (decibels). |
NFactor, K, Mu, and MuPrime. | None |
NTemp | Kelvin |
Gt, Ga, Gp, Gmag, and Gmsg. | dB, Magnitude (decibels), and None. |
Dependencies
To enable Y format1, set Plot type to X-Y plane.
Plot format, specified as one of the following.
| Y parameter2 | Y format2 |
|---|---|
S11, S12, S21, S22, GammaIn, GammaOut, TF1, TF2, TF3, GammaMS, GammaML, and Delta. | dB, Magnitude (decibels), Abs, Mag, Magnitude (linear), Angle, Angle(degrees), Angle(radians), Real, Imag, and Imaginary. |
GroupDelay | ns, us, ms, s, and ps. |
VSWRIn and VSWROut. | Magnitude (decibels) and None. |
OIP3 and IIP3. | dBm, W, and mW. |
NF | dB and Magnitude (decibels). |
NFactor, K, Mu, and MuPrime. | None |
NTemp | Kelvin |
Gt, Ga, Gp, Gmag, and Gmsg. | dB, Magnitude (decibels), and None. |
Dependencies
To enable Y format2, set Plot type to X-Y plane.
Frequency plot, specified as Freq.
Frequency plot format, specified as one of the following.
Auto | Hz | kHz | MHz |
GHz | THz |
Y-axis scale, specified as Linear or Log.
Dependencies
To enable this parameter, set Plot type to X-Y
plane.
X-axis scale, specified as Linear or Log.
Dependencies
To enable this parameter, set Plot type to X-Y
plane.
Plot the specified data using the plot button.
References
[1] Ludwig, Reinhold and Pavel Bretchko, RF Circuit Design: Theory and Applications, Prentice-Hall, 2000.
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Website auswählen
Wählen Sie eine Website aus, um übersetzte Inhalte (sofern verfügbar) sowie lokale Veranstaltungen und Angebote anzuzeigen. Auf der Grundlage Ihres Standorts empfehlen wir Ihnen die folgende Auswahl: .
Sie können auch eine Website aus der folgenden Liste auswählen:
So erhalten Sie die bestmögliche Leistung auf der Website
Wählen Sie für die bestmögliche Website-Leistung die Website für China (auf Chinesisch oder Englisch). Andere landesspezifische Websites von MathWorks sind für Besuche von Ihrem Standort aus nicht optimiert.
Amerika
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)