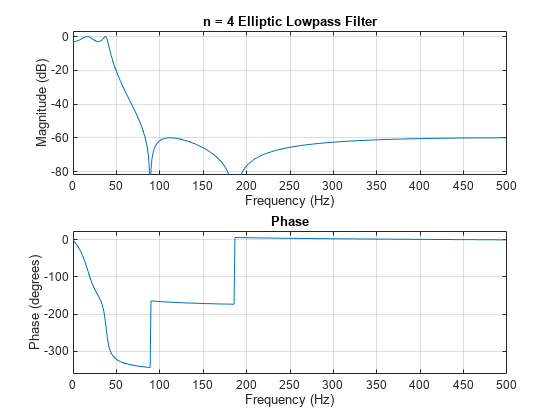
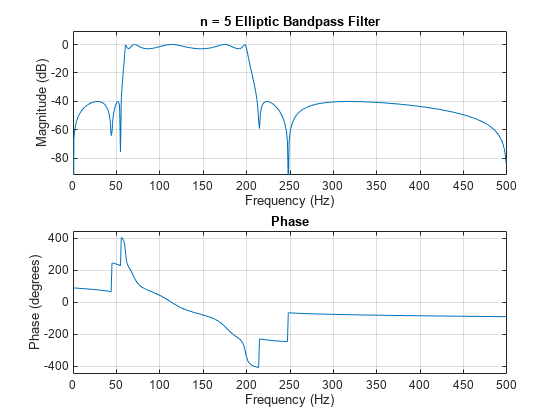
ellipord

Minimum order for elliptic filters

collapse all in page

Syntax

[n,Wn] = ellipord(Wp,Ws,Rp,Rs)
[n,Wn] = ellipord(Wp,Ws,Rp,Rs,'s')

Description

[n,Wn] = ellipord(Wp,Ws,Rp,Rs) returns the lowest order, n, of the digital elliptic filter with no more than Rp dB of passband ripple and at least Rs dB of attenuation in the stopband. Wp and Ws, are respectively, the passband and stopband edge frequencies of the filter, normalized from 0 to 1, where 1 corresponds to π rad/sample. The scalar (or vector) of corresponding cutoff frequencies, Wn, is also returned. To design an elliptic filter, use the output arguments n and Wn as inputs to ellip.

example

[n,Wn] = ellipord(Wp,Ws,Rp,Rs,'s') finds the minimum order n and cutoff frequencies Wn for an analog elliptic filter. Specify the frequencies Wp and Ws in radians per second. The passband or the stopband can be infinite.

Examples

collapse all

Open Live Script

For 1000 Hz data, design a lowpass filter with less than 3 dB of ripple in the passband, defined from 0 to 40 Hz, and at least 60 dB of ripple in the stopband, defined from 150 Hz to the Nyquist frequency, 500 Hz. Find the filter order and cutoff frequency.

Wp = 40/500;
Ws = 150/500;
Rp = 3;
Rs = 60;
[n,Wp] = ellipord(Wp,Ws,Rp,Rs)
n = 
4

Wp = 
0.0800

Specify the filter in terms of second-order sections and plot the frequency response.

[z,p,k] = ellip(n,Rp,Rs,Wp);
sos = zp2sos(z,p,k);
freqz(sos,512,1000)
title(sprintf('n = %d Elliptic Lowpass Filter',n))

Figure contains 2 axes objects. Axes object 1 with title Phase, xlabel Frequency (Hz), ylabel Phase (degrees) contains an object of type line. Axes object 2 with title n = 4 Elliptic Lowpass Filter, xlabel Frequency (Hz), ylabel Magnitude (dB) contains an object of type line.

Open Live Script

Design a bandpass filter with a passband from 60 Hz to 200 Hz with at most 3 dB of ripple and at least 40 dB attenuation in the stopbands. Specify a sampling rate of 1 kHz. Have the stopbands be 50 Hz wide on both sides of the passband. Find the filter order and cutoff frequencies.

Wp = [60 200]/500;
Ws = [50 250]/500;
Rp = 3;
Rs = 40;

[n,Wp] = ellipord(Wp,Ws,Rp,Rs)
n = 
5

Wp = 1×2

    0.1200    0.4000

Specify the filter in terms of second-order sections and plot the frequency response.

[z,p,k] = ellip(n,Rp,Rs,Wp);
sos = zp2sos(z,p,k);

freqz(sos,512,1000)
title(sprintf('n = %d Elliptic Bandpass Filter',n))

Figure contains 2 axes objects. Axes object 1 with title Phase, xlabel Frequency (Hz), ylabel Phase (degrees) contains an object of type line. Axes object 2 with title n = 5 Elliptic Bandpass Filter, xlabel Frequency (Hz), ylabel Magnitude (dB) contains an object of type line.

Input Arguments

collapse all

Passband corner (cutoff) frequency, specified as a scalar or a two-element vector with values between 0 and 1, with 1 corresponding to the normalized Nyquist frequency, π rad/sample.

  • If Wp and Ws are both scalars and Wp < Ws, then ellipord returns the order and cutoff frequency of a lowpass filter. The stopband of the filter ranges from Ws to 1 and the passband ranges from 0 to Wp.

  • If Wp and Ws are both scalars and Wp > Ws, then ellipord returns the order and cutoff frequency of a highpass filter. The stopband of the filter ranges from 0 to Ws and the passband ranges from Wp to 1.

  • If Wp and Ws are both vectors and the interval specified by Ws contains the one specified by Wp (Ws(1) < Wp(1) < Wp(2) < Ws(2)), then ellipord returns the order and cutoff frequencies of a bandpass filter. The stopband of the filter ranges from 0 to Ws(1) and from Ws(2) to 1. The passband ranges from Wp(1) to Wp(2).

  • If Wp and Ws are both vectors and the interval specified by Wp contains the one specified by Ws (Wp(1) < Ws(1) < Ws(2) < Wp(2)), then ellipord returns the order and cutoff frequencies of a bandstop filter. The stopband of the filter ranges from Ws(1) to Ws(2). The passband ranges from 0 to Wp(1) and from Wp(2) to 1.

Data Types: single | double

Note

If your filter specifications call for a bandpass or bandstop filter with unequal ripple in each of the passbands or stopbands, design separate lowpass and highpass filters and cascade the two filters together.

Stopband corner frequency, specified as a scalar or a two-element vector with values between 0 and 1, with 1 corresponding to the normalized Nyquist frequency, π rad/sample.

Data Types: single | double

Passband ripple, specified as a scalar expressed in dB.

Data Types: single | double

Stopband attenuation, specified as a scalar expressed in dB.

Data Types: single | double

Output Arguments

collapse all

Lowest filter order, returned as an integer scalar.

Cutoff frequencies, returned as a scalar or vector.

Algorithms

ellipord uses the elliptic lowpass filter order prediction formula described in [1]. The function performs its calculations in the analog domain for both the analog and digital cases. For the digital case, it converts the frequency parameters to the s-domain before estimating the order and natural frequencies, and then converts them back to the z-domain.

ellipord initially develops a lowpass filter prototype by transforming the passband frequencies of the desired filter to 1 rad/s (for low and highpass filters) and to –1 and 1 rad/s (for bandpass and bandstop filters). It then computes the minimum order required for a lowpass filter to meet the stopband specification.

References

[1] Rabiner, Lawrence R., and B. Gold. Theory and Application of Digital Signal Processing. Englewood Cliffs, NJ: Prentice Hall, 1975.

Extended Capabilities

expand all

Version History

Introduced before R2006a

See Also

| | |