slantRangeCircularOrbit
Calculate slant range or distance between circularly orbiting satellite and ground station
Since R2024a
Description
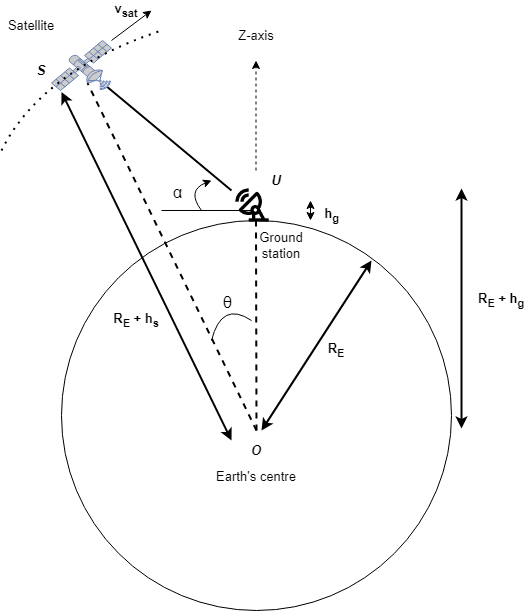
dist = slantRangeCircularOrbit(el,hs,hg)el, satellite altitude
hs, and ground station altitude hg.
For more information, see Slant Range Calculations.
Note
slantRangeCircularOrbitassumes the Earth is spherical and ignores the Earth rotation rate.slantRangeCircularOrbitalso assumes that an access or link is possible from the satellite to the ground station at all times.You can apply this syntax to any orbit type irrespective of its shape.
dist = slantRangeCircularOrbit(el,hs,hg,time)
For more information, see Slant Range Calculations.
Note
This syntax also assumes:
The ground station is located at the North Pole (positive Z–axis), and the satellite starts from the initial input elevation angle
elin the second quadrant of the YZ–plane.Satellite moves in the clockwise direction in its circular orbit.
Examples
Input Arguments
Output Arguments
More About
Extended Capabilities
Version History
Introduced in R2024a