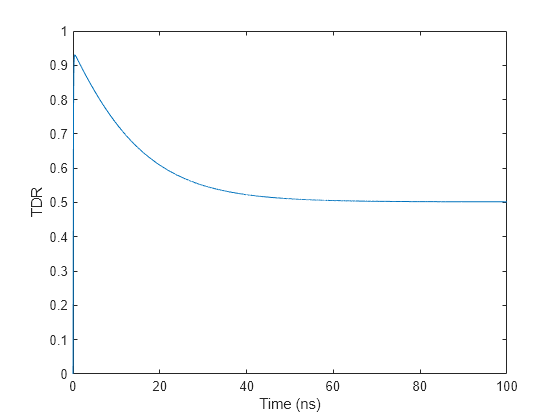
stepresp
Step-signal response for rational object and rationalfit function
object
Description
Examples
Input Arguments
Output Arguments
More About
Version History
Introduced in R2010a
See Also
freqresp | pwlresp | rationalfit | makepassive | writeva | ispassive | rfmodel.rational