Train Hybrid SAC Agent for Path-Following Control

Open Live Script

This example shows how to train a hybrid soft actor-critic (SAC) agent to perform path-following control (PFC) for a vehicle. A hybrid agent is an agent that has an action space that is partly discrete and partly continuous.

Overview

The goals of the PFC system are to make the ego vehicle travel at a set velocity, maintain a safe distance from a lead car by controlling longitudinal acceleration and braking, and travel along the centerline of its lane by controlling the front steering angle. An example that trains two RL agents (one with discrete action space, the other with continuous action space) to perform PFC is shown in Train Multiple Agents for Path Following Control. In that example, a DDPG agent provides continuous acceleration values for the longitudinal control loop while a DQN agent provides discrete steering angle values for the lateral control loop. For a PFC example that uses a single continuous action space for both longitudinal speed and lateral steering, see Train DDPG Agent for Path-Following Control. For more information on PFC systems, see Path Following Control System (Model Predictive Control Toolbox).

In this example, a single hybrid SAC agent is trained to control both the lateral steering (discrete action) the longitudinal speed (continuous action) of the ego vehicle. For more information about SAC agents, see Soft Actor-Critic (SAC) Agent.

Fix Random Number Stream for Reproducibility

The example code might involve computation of random numbers at various stages. Fixing the random number stream at the beginning of various sections in the example code preserves the random number sequence in the section every time you run it, and increases the likelihood of reproducing the results. For more information, see Results Reproducibility.

Fix the random number stream with seed 0 and random number algorithm Mersenne twister. For more information on controlling the seed used for random number generation, see rng.

previousRngState = rng(0,"twister");

The output previousRngState is a structure that contains information about the previous state of the stream. You will restore the state at the end of the example.

Create Environment Object

The environment for this example includes a simple bicycle model for the ego car and a simple longitudinal model for the lead car. The agent controls the ego car's longitudinal acceleration, braking, and the front steering angle.

Load the environment parameters.

hybridAgentPFCParams

Open the Simulink® model.

mdl = "rlHybridAgentPFC";
open_system(mdl)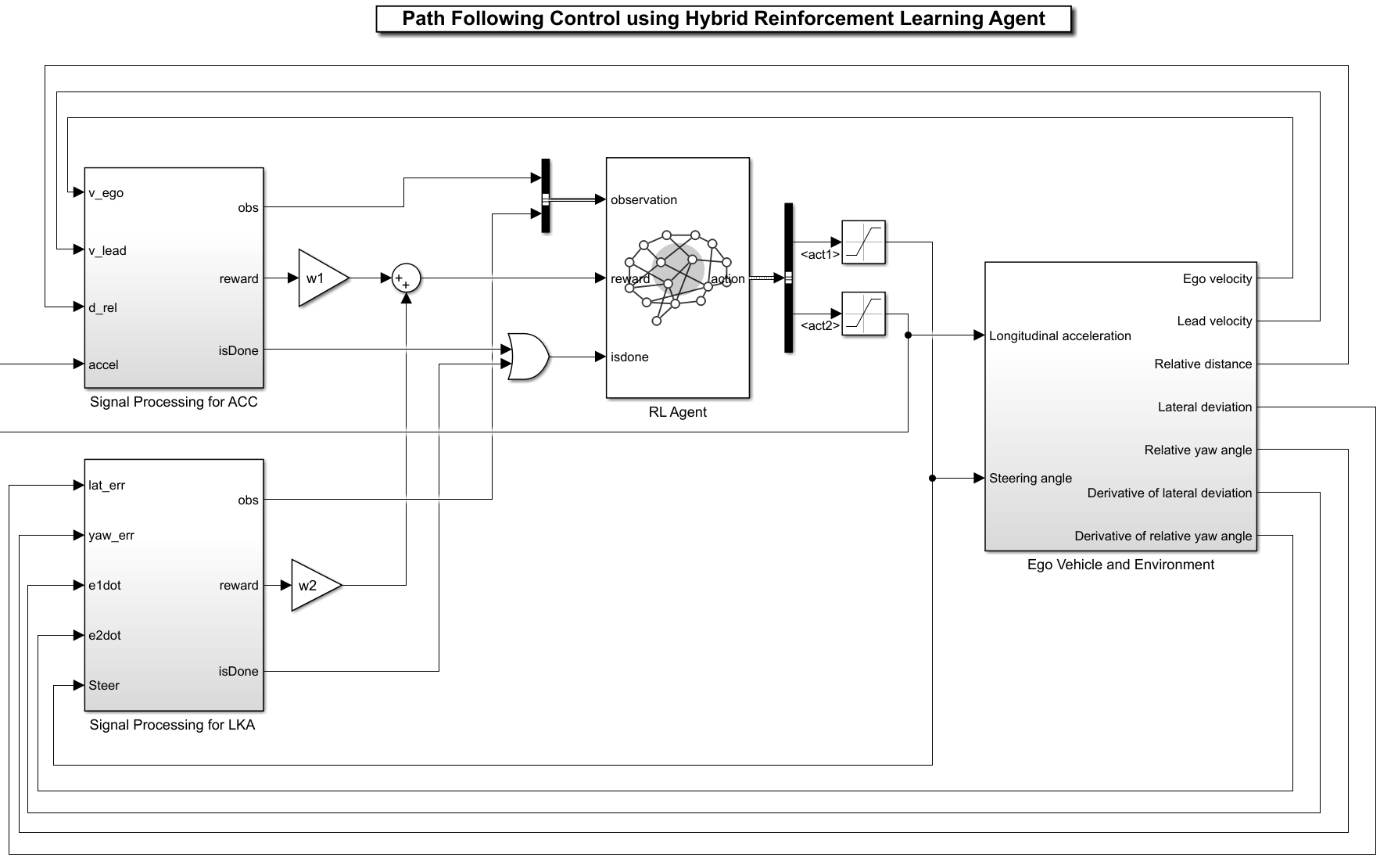

The simulation terminates if any of the following conditions occur.

$| e_{1} | > 1$ — magnitude of the lateral deviation is greater than 1.
$V_{e g o} < 0.5$ — longitudinal velocity of the ego car is less than 0.5.
$D_{r e l} < 0$ — distance between the ego and the lead car is less than zero.

To determine the ego car's reference velocity $V_{r e f}$ :

The safe distance is a linear function of the ego car's longitudinal velocity $V$ , that is, $t_{g a p} * V + D_{d e f a u l t}$ .
If the relative distance is less than the safe distance, the ego car tracks the minimum value between the velocity of the lead car and the desired velocity set by the driver. Setting the reference velocity in this way allows the ego car to maintain a safe distance from the lead car. If the relative distance is greater than the safe distance, the ego car uses the desired velocity set by the driver as the reference velocity.

Observation:

The first observation channel contains the longitudinal measurements — the velocity error $e_{V} = V_{r e f} - V$ , its integral $\int e$ , and the ego car longitudinal velocity $V$ .
The second observation channel contains the lateral measurements — the lateral deviation $e_{1}$ , relative yaw angle $e_{2}$ (the yaw angle error with respect to the lane centerline), their derivatives ${e_{}^{˙}}_{1}$ and ${e_{}^{˙}}_{2}$ , and their integrals $\int e_{1}$ and $\int e_{2}$ .

Action:

The discrete action $a_{t}$ — The action signal consists of discrete steering angle actions which take values from –15 degrees (–0.2618 rad) to 15 degrees (0.2618 rad) in steps of 1 degree (0.0175 rad).
The continuous action $u_{t}$ — The action signal consists of continuous acceleration values between –3 and 2 $m / s^{2}$ .

Reward:

The reward $r_{t}$ , provided at every time step $t$ , is the weighted sum of the reward $r_{lateral}$ for the lateral control and the reward $r_{longitudinal}$ for the longitudinal control.

$\begin{array}{l} r_{t} = w_{1} r_{l a t e r a l} + w_{2} r_{l o n g i t u d i n a l} \\ r_{l a t e r a l} = - (100 e_{1}^{2} + 500 u_{t - 1}^{2}) \times 0.001 - 10 F_{t} + 2 H_{t} \\ r_{l o n g i t u d i n a l} = - (10 e_{V}^{2} + 100 a_{t - 1}^{2}) \times 0.001 - 10 F_{t} + M_{t} \\ w_{1} = 1 / 12 \\ w_{2} = 1 / 5 \end{array}$

In these equations, $u_{t - 1}$ is the steering input from the previous time step, $a_{t - 1}$ is the acceleration input from the previous time step, and:

$F_{t} = 1$ if the simulation terminates, otherwise $F_{t} = 0$ .
$M_{t} = 1$ if $e_{V}^{2} < 1$ , otherwise $M_{t} = 0$ .
$H_{t} = 1$ if $e_{1}^{2} < 0.01$ , otherwise $H_{t} = 0$ .

The logical terms in the reward functions ( $F_{t}$ , $M_{t}$ , and $H_{t}$ ) penalize the agent if the simulation terminates early, while encouraging the agent to make both the lateral error and velocity error small.

Create the observation specification. Because an observation contains multiple channels in this Simulink environment, you must use the bus2RLSpec function to create the specification .

Create a bus object.

obsBus = Simulink.Bus();

Add the first bus element.

obsBus.Elements(1) = Simulink.BusElement;
obsBus.Elements(1).Name = "signal1";
obsBus.Elements(1).Dimensions = [3,1];

Add the second bus element.

obsBus.Elements(2) = Simulink.BusElement;
obsBus.Elements(2).Name = "signal2";
obsBus.Elements(2).Dimensions = [6,1];

Create the observation specification.

obsInfo= bus2RLSpec("obsBus");

Create the action specification. For the hybrid SAC agent, you must have two action channels. The first action channel must be for the discrete part of the action, and the second must be for the continuous part of the action. Use the bus2RLSpec function to create the specification, as for the observation specification case.

Create a bus object.

actBus = Simulink.Bus();

Add the first bus element for the discrete action.

actBus.Elements(1) = Simulink.BusElement;
actBus.Elements(1).Name = "act1";

Add the second bus element for the continuous action.

actBus.Elements(2) = Simulink.BusElement;
actBus.Elements(2).Name = "act2";
actBus.Elements(2).Dimensions = [1,1];
actInfo = bus2RLSpec("actBus","DiscreteElements",...
           {"act1",(-15:15)*pi/180});

Define the limits of continuous actions.

actInfo(2).LowerLimit = -3;
actInfo(2).UpperLimit = 2;

Create a Simulink environment object, specifying the block paths for the agent block. For more information, see rlSimulinkEnv.

blks = mdl + "/RL Agent";
env = rlSimulinkEnv(mdl,blks,obsInfo,actInfo);

Specify a reset function for the environment using the ResetFcn property. The function pfcResetFcn (provided at the end of the example) sets the initial conditions of the lead and ego vehicles at the beginning of every episode during training.

env.ResetFcn = @pfcResetFcn;

Create Hybrid SAC Agent

Fix the random number stream.

rng(0, "twister");

Set the sample time, in seconds, for the Simulink model and the RL agent object.

Ts = 0.1;

Create a default hybrid SAC agent. When the action specification defines an hybrid action space (that is contains both a discrete and a continuous action channel), rlSACAgent creates an hybrid SAC agent.

agent = rlSACAgent(obsInfo, actInfo);

Specify the agent options:

Set the mini-batch size to 128 to make the training more stable (at the expense of larger memory requirement).
Use a maximum of 200 mini-batches to update the agent at the end of each episode. The default LearningFrequency is -1, meaning that the agent updates at the end of each episode.
Set learning rate to 1e-3 for the actor and the critics.
Set gradient thresholds to 1 to limit the gradient values.
Use an experience buffer that can store 1 million experiences. A large experience buffer can contain diverse experiences.
Set the number of steps for the Q-value estimate (NumStepsToLookAhead) to 3 to accurately estimate the Q-value.
Set the initial entropy weights for discrete actions and continuous actions to 0.1 to achieve a better balance between exploitation and exploration early in training.

agent.SampleTime = Ts;
agent.AgentOptions.MiniBatchSize = 128;
agent.AgentOptions.MaxMiniBatchPerEpoch = 200;
agent.AgentOptions.ActorOptimizerOptions.LearnRate = 1e-3;
agent.AgentOptions.ActorOptimizerOptions.GradientThreshold = 1;
agent.AgentOptions.CriticOptimizerOptions(1).LearnRate = 1e-3;
agent.AgentOptions.CriticOptimizerOptions(1).GradientThreshold = 1;
agent.AgentOptions.CriticOptimizerOptions(2).LearnRate = 1e-3;
agent.AgentOptions.CriticOptimizerOptions(2).GradientThreshold = 1;
agent.AgentOptions.ExperienceBufferLength = 1e6;
agent.AgentOptions.NumStepsToLookAhead = 3;

Set the initial entropy weight for the discrete and continuous actions.

agent.AgentOptions.EntropyWeightOptions(1).EntropyWeight = 0.1;
agent.AgentOptions.EntropyWeightOptions(2).EntropyWeight = 0.1;

Train hybrid SAC Agent

Specify the training options. For this example, use the following options.

Run each training episode for a maximum of 5000 episodes, with each episode lasting a maximum of maxsteps time steps.
Display the training progress in the Reinforcement Learning Training Monitor dialog box.
Stop training when the agent receives an average evaluation episode reward greater than 196.
To improve performance, do not save the simulation data during training. To save the simulation data during training instead, set SimulationStorageType to "file" or "memory".

Tf = 60; % Simulation time
maxepisodes = 5000;
maxsteps = ceil(Tf/Ts);
trainingOpts = rlTrainingOptions( ...        
    MaxEpisodes=maxepisodes, ...
    MaxStepsPerEpisode=maxsteps, ...
    StopTrainingCriteria="EvaluationStatistic", ...
    StopTrainingValue= 196, ...
    SimulationStorageType="none");

Fix the random number stream.

rng(0, "twister");

Train the agent using the train function. Training the agent is a computationally intensive process that takes a couple of hours to complete. To save time while running this example, load a pretrained agent by setting doTraining to false. To train the agent yourself, set doTraining to true.

doTraining = false;
if doTraining    
    % Evaluate the agent after every 25 training episodes. 
    % The evaluation statistic is the mean value of 
    % the statistic over five evaluation episodes.    
    evaluator = rlEvaluator(EvaluationFrequency=25, ...
        NumEpisodes=5, RandomSeeds=[101:105]);

    % Train the agent.
    trainingStats = train(agent,env,trainingOpts,Evaluator=evaluator);
else
    % Load the pretrained agent for the example.
    load("rlHybridPFCAgent.mat")       
end

The figure shows a snapshot of the training progress.

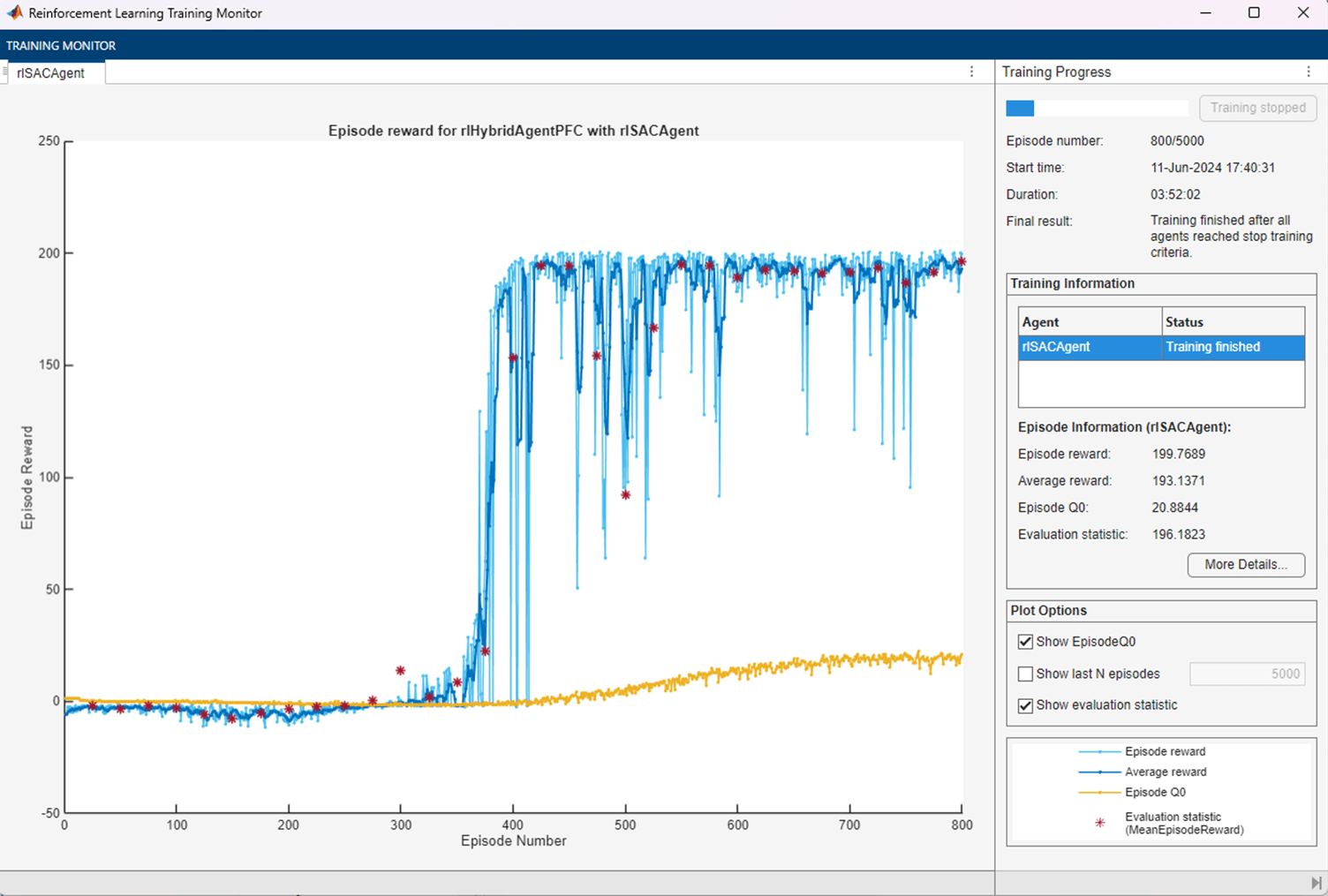
Simulate the trained SAC Agent

Fix the random number stream.

rng(0, "twister");

To validate the performance of the trained agent, simulate the agent within the Simulink environment. For more information on agent simulation, see rlSimulationOptions and sim.

agent.UseExplorationPolicy = false;
simOptions = rlSimulationOptions(MaxSteps=maxsteps);
experience = sim(env,agent,simOptions);

To demonstrate the trained agent using deterministic initial conditions, simulate the model in Simulink.

e1_initial = -0.4;
e2_initial = 0.1;
x0_lead = 70;
sim(mdl)

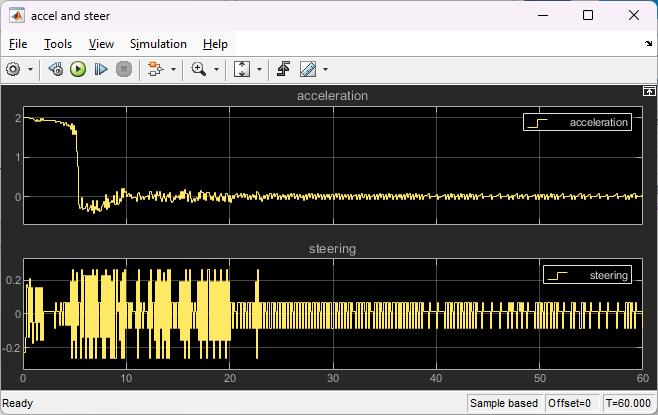
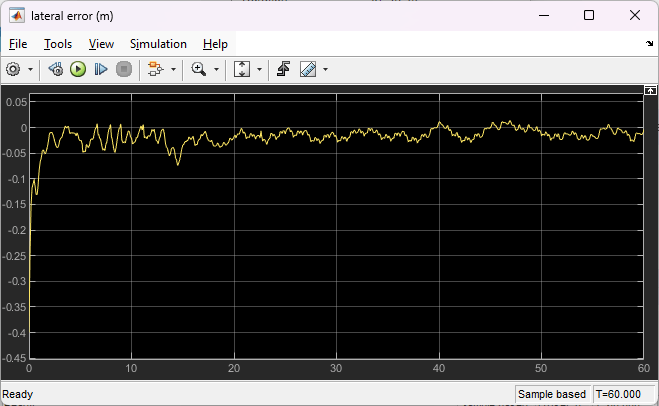
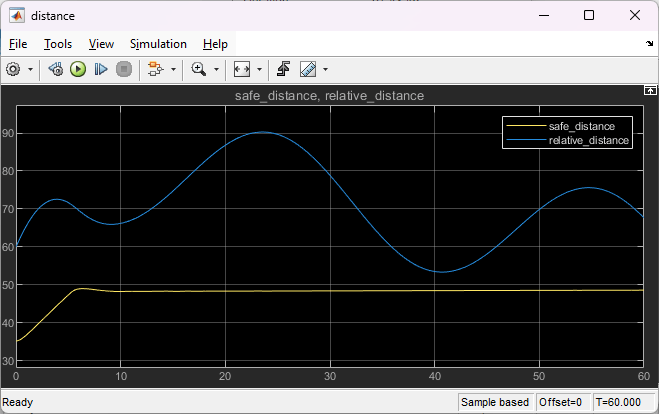
The plots show the results when the lead car is 70 m ahead of the ego car at the beginning of the simulation.

The lead car changes speed from 24 m/s to 30 m/s periodically (see the "velocity" plot).
From 0 to 10 seconds, the ego car tracks the set velocity (see the "velocity" plot) and experiences some acceleration ("accel and steer" plot). After 10 seconds, the acceleration is close to 0.
The lateral deviation decreases greatly within 1 second and remains less than 0.1 m (see the "lateral error" plot).
The ego car maintains a safe distance throughout the simulation (see "distance" plot).

Restore the random number stream using the information stored in previousRngState.

rng(previousRngState)

Environment Reset Function

function in = pfcResetFcn(in)

    % random value for initial position of lead car
    in = setVariable(in,'x0_lead',40+randi(60,1,1));

    % random value for lateral deviation
    in = setVariable(in,'e1_initial', 0.5*(-1+2*rand));

    % random value for relative yaw angle
    in = setVariable(in,'e2_initial', 0.1*(-1+2*rand));

end

Train Hybrid SAC Agent for Path-Following Control

Overview

Fix Random Number Stream for Reproducibility

Create Environment Object

Create Hybrid SAC Agent

Train hybrid SAC Agent

Simulate the trained SAC Agent

Environment Reset Function

See Also

Functions

Objects

Blocks

Topics