minvarweights

Weights for minimum-variance array pattern synthesis

Syntax

wts = minvarweights(pos,ang)

wts = minvarweights(pos,angcov)

wts = minvarweights(___,MaskAngle=angm)

wts = minvarweights(___,MaskSidelobeLevel=sllm)

wts = minvarweights(___,NullAngle=angn)

Description

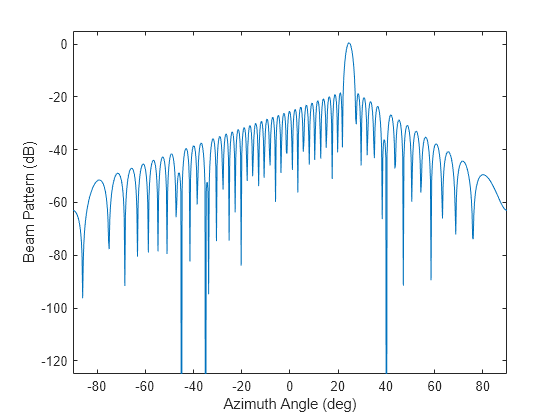
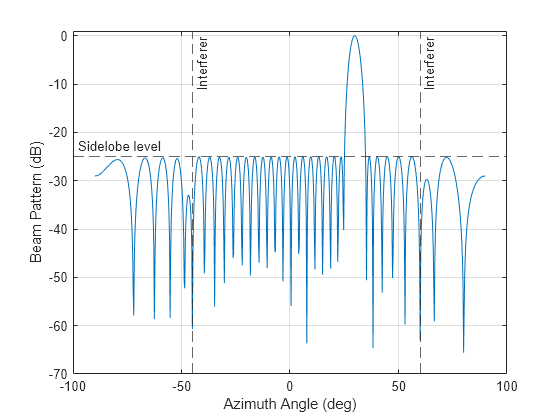
wts = minvarweights(pos,ang) computes the minimum-variance weights wts for synthesizing the pattern of a sensor array in the directions specified by ang. Array element positions are specified in pos. The function optimizes the beamforming weights using a second-order cone programming solver.

wts = minvarweights(pos,angcov) also specifies the spatial covariance matrix cov of the array elements.

wts = minvarweights(___,MaskAngle=angm) also specifies angles angm at which mask sidelobe levels are defined in the sllm argument.

wts = minvarweights(___,MaskSidelobeLevel=sllm) also specifies maximum allowable sidelobe levels sllm at the angles defined in angm.

wts = minvarweights(___,NullAngle=angn) also specifies null directions angn for the array.

Examples

Compute Optimized ULA Beamforming Weights

Compute optimized beamforming weights of a 31-element half-wavelength spacing ULA in the direction of ${-30}^{\circ }$ degree in azimuth. Design the array to keep sidelobe levels less than -23 dB.

Create the optimized weights.

N = 31;
pos = (0:N-1)*0.5;
sll = -23;
wts = minvarweights(pos,-30,MaskSidelobeLevel=sll);

Apply the optimized weights and display the array pattern from $-{90}^{\circ }$ to ${+90}^{\circ }$ azimuth.

az = -90:.25:90;
pat_opt = arrayfactor(pos,az,wts);
plot(az,mag2db(abs(pat_opt)))
xlabel('Azimuth Angle (deg)')
ylabel('Beam Pattern (dB)')
xlim([-90,90])

Optimized Tapered ULA Weights

Design an array to have a tapered beampattern, The array is a 51-element half-wavelength spacing ULA steered in the direction of ${25}^{\circ }$ in azimuth. The pattern synthesis goal is to achieve sidelobe levels smaller than a tapered mask decreasing linearly from -18 dB to -55 dB at $\pm {90}^{\circ }$. Place nulls at ${-35}^{\circ }$, $-{45}^{\circ }$, and ${40}^{\circ }$ azimuth angle.

N = 51;
pos = (0:N-1)*0.5;
ANGmainBeam = 25;
angn = [-35 -45 40];
angm = [-90:.2:22 27:0.2:90];
sllm = [linspace(-55,-18,length(-90:.2:22)) ...
    linspace(-18,-55,length(27:.2:90))];
wts = minvarweights(pos,ANGmainBeam,'MaskAngle',angm, ...
    'MaskSidelobeLevel',sllm,'NullAngle',angn);

Apply optimized weights and display the array pattern from ${-90}^{\circ }$ to ${+90}^{\circ }$ in azimuth.

az = -90:.25:90;
pat_opt = arrayfactor(pos,az,wts);
plot(az,mag2db(abs(pat_opt)))
axis([-90 90 -125 5])
xlabel('Azimuth Angle (deg)')
ylabel('Beam Pattern (dB)')

Verify that nulls are placed at ${-35}^{\circ }$, $-{45}^{\circ }$, and ${40}^{\circ }$ azimuth angle.

Input Arguments

pos — Positions of array sensor elements

1-by-N real-valued vector | 2-by-N real-valued matrix | 3-by-N real-valued matrix

Positions of the elements of a sensor array, specified as a 1-by-N vector, a 2-by-N matrix, or a 3-by-N matrix. In this vector or matrix, N represents the number of elements of the array. Each column of pos represents the coordinates of an element. If pos is a 1-by-N vector, then it represents the y-coordinate of the sensor elements of a line array. The x and z-coordinates are assumed to be zero. When pos is a 2-by-N matrix, it represents the (y,z)-coordinates of the sensor elements of a planar array. This array is assumed to lie in the yz-plane. The x-coordinates are assumed to be zero. When pos is a 3-by-N matrix, then the array can have an arbitrary shape. Sensor positions are in terms of signal wavelength.

Example: [0,0,0; 0.1,0.4,0.3; 1,1,1]

Data Types: double

ang — Beamforming directions

1-by-M real-valued vector | 2-by-M real-valued matrix

Beamforming directions, specified as a 1-by-M vector or a 2-by-M matrix. In this vector or matrix, M represents the number of incoming signals. If ang is a 2-by-M matrix, each column specifies the direction in azimuth and elevation of the beamforming direction as [az;el]. Angular units are specified in degrees. The azimuth angle must lie between –180° and 180° and the elevation angle must lie between –90° and 90°. The azimuth angle is the angle between the x-axis and the projection of the beamforming direction vector onto the xy plane. The angle is positive when measured from the x-axis toward the y-axis. The elevation angle is the angle between the beamforming direction vector and xy-plane. It is positive when measured towards the positive z axis. If ang is a 1-by-M vector, then it represents a set of azimuth angles with the elevation angles assumed to be zero.

Example: [45;10]

Data Types: double

cov — Sensor spatial covariance matrix

eye(N) (default) | N-by-N complex-valued matrix

Sensor spatial covariance matrix, specified as an N-by-N complex-valued matrix. N is the number of array sensor elements.

Example: [5,0.1;0.1,2]

Data Types: double
Complex Number Support: Yes

angm — Mask angles

[] (default) | real-valued 1-by-K vector | real-valued 2-by-K matrix

Angles at which mask sidelobe levels are defined, specified as a real-valued 1-by-K vector or a real-valued 2-by-K matrix where K is the number of mask sidelobe levels. If angm is a 1-by-K vector, then it contains the azimuth angles of the mask directions. If angm is a 2-by-K matrix, each column specifies the direction in the form [az;el]. Angle units are in degrees.

Data Types: double

sllm — Maximum allowable mask sidelobe levels

non-positive scalar (default) | non-positive real-valued 1-by-K vector

Maximum allowable mask sidelobe levels, specified as a non-positive scalar or non-positive real-valued 1-by-K vector. K is the number of mask sidelobe levels. Sidelobe levels are always less then or equal to zero.

• If sllm is a scalar, then it contains a uniform mask for all sidelobe levels and angm must be empty.

• If sllm is a 1-by-K vector, then sllm and angm must have the same number of columns; and sllm contains the mask sidelobe levels for corresponding mask angles, angm.

An empty sllm vector means that there are no constraints on the sidelobe levels. Units are in dB.

Data Types: double

angn — Null direction angles

[] (default) | real-valued 1-by-P vector | real-valued 2-by-P matrix

Null direction angles, specified as either a 1-by-P vector or a 2-by-P matrix where P is the number of null directions. If angn is a 1-by-P vector, then it contains only the azimuth angles of directions. If angn is a 2-by-P matrix, each column specifies the null direction in the form [az; el]. Angle units are in degrees.

Data Types: double

Output Arguments

wts — Beamformer weights

N-by-1 complex-valued vector

Beamformer weights, returned as a complex-valued N-by-1 vector. N represents the number of sensor elements of the array.

References

[1] Lebret, H., and S. Boyd. “Antenna Array Pattern Synthesis via Convex Optimization.” IEEE Transactions on Signal Processing, vol. 45, no. 3, Mar. 1997, pp. 526–32. DOI.org (Crossref), https://doi.org/10.1109/78.558465.

[2] Golbon-Haghighi, Mohammad-Hossein, et al. “Design of a Cylindrical Crossed Dipole Phased Array Antenna for Weather Surveillance Radars.” IEEE Open Journal of Antennas and Propagation, vol. 2, 2021, pp. 402–11. DOI.org (Crossref), https://doi.org/10.1109/OJAP.2021.3059471.

Version History

Introduced in R2022b